Boy's surface
Encyclopedia
In geometry
, Boy's surface is an immersion of the real projective plane
in 3-dimensional space found by Werner Boy
in 1901 (he discovered it on assignment from David Hilbert
to prove that the projective plane could not be immersed in 3-space
). Unlike the Roman surface
and the cross-cap
, it has no singularities (i.e., pinch-points
), but it does self-intersect.
To make a Boy's surface:
Boy's surface is discussed (and illustrated) in Jean-Pierre Petit
's Le Topologicon.
Boy's surface was first parametrized explicitly by Bernard Morin
in 1978. See below for another parametrization, discovered by Rob Kusner and Robert Bryant.
. This means that it has an axis of discrete rotational symmetry: any 120° turn about this axis will leave the surface looking exactly the same. The Boy's surface can be cut into three mutually congruent
pieces.
has a large model of a Boy's surface outside the entrance, constructed and donated by Mercedes-Benz
in January 1991. This model has 3-fold rotational symmetry
and minimizes the Willmore energy
of the surface. It consists of steel strips which represent the image of a polar coordinate grid
under a parameterization given by Robert Bryant and Rob Kusner. The meridians (rays) become ordinary Möbius strip
s, i.e. twisted by 180 degrees. All but one of the strips corresponding to circles of latitude (radial circles around the origin) are untwisted, while the one corresponding to the boundary of the unit circle is a Möbius strip twisted by three times 180 degrees — as is the emblem of the institute .
, is the following: given a complex number z whose magnitude
is less than or equal to one (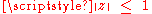
), let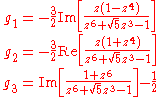
so that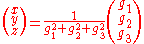
where x, y, and z are the desired Cartesian coordinates of a point on the Boy's surface.
If one performs an inversion of this parametrization centered on the triple point, one obtains a complete minimal surface
with three "ends" (that's how this parametrization was discovered naturally). This implies that the Bryant-Kusner parametrization of Boy's surfaces is "optimal" in the sense that it is the "least bent" immersion of a projective plane into three-space.
,
then the functions g1, g2, and g3 of z are left unchanged.
, where 
denote a point
on Boy's surface. Then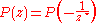
but only if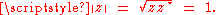
What if 
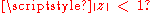Then
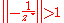
because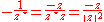
whose magnitude is
but
so that
Since P(z) belongs to the Boy's surface only when
, this means that 
belongs to Boy's surface only if 
Thus 
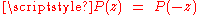if 
but all other points on the Boy's surface are unique. The set of complex values 
is the unit disk, Thus the Boy's surface has been parametrized by a disk such that pairs of diametrically opposite points on the perimeter
of the disk are equivalent. Therefore the Boy's surface is homeomorphic
to the real projective plane
, RP2.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, Boy's surface is an immersion of the real projective plane
Real projective plane
In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
in 3-dimensional space found by Werner Boy
Werner Boy
Werner Boy was a German mathematician. He was the discoverer and eponym of Boy's surface — a three dimensional projection of the real projective plane without singularities, the first of its kind...
in 1901 (he discovered it on assignment from David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
to prove that the projective plane could not be immersed in 3-space
Three-dimensional space
Three-dimensional space is a geometric 3-parameters model of the physical universe in which we live. These three dimensions are commonly called length, width, and depth , although any three directions can be chosen, provided that they do not lie in the same plane.In physics and mathematics, a...
). Unlike the Roman surface
Roman surface
The Roman surface is a self-intersecting mapping of the real projective plane into three-dimensional space, with an unusually high degree of symmetry...
and the cross-cap
Cross-cap
In mathematics, a cross-cap is a two-dimensional surface that is a model of a Möbius strip with a single self intersection. This self intersection precludes the cross-cap from being topologically equivalent to a Möbius strip...
, it has no singularities (i.e., pinch-points
Pinch point (mathematics)
right|frame|240px|Section of the [[Whitney umbrella]], an example of pinch point singularity.In geometry, a pinch point or cuspidal point is a type of singular point on an algebraic surface....
), but it does self-intersect.
To make a Boy's surface:
- Start with a sphere. Remove a cap.
- Attach one end of each of three strips to alternate sixths of the edge left by removing the cap.
- Bend each strip and attach the other end of each strip to the sixth opposite the first end, so that the inside of the sphere at one end is connected to the outside at the other. Make the strips skirt the middle rather than go through it.
- Join the loose edges of the strips. The joins intersect the strips.
Boy's surface is discussed (and illustrated) in Jean-Pierre Petit
Jean-Pierre Petit
Jean-Pierre Petit is a French scientist, senior researcher at National Center for Scientific Research as an astrophysicist in Marseille Observatory, now retired...
's Le Topologicon.
Boy's surface was first parametrized explicitly by Bernard Morin
Bernard Morin
Bernard Morin is a French mathematician, specifically a topologist, born in 1931, who is now retired. He has been blind since age 6 due to glaucoma, but his blindness did not prevent him from having a successful career in mathematics....
in 1978. See below for another parametrization, discovered by Rob Kusner and Robert Bryant.
Symmetry of the Boy's surface
Boy's surface has 3-fold symmetrySymmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
. This means that it has an axis of discrete rotational symmetry: any 120° turn about this axis will leave the surface looking exactly the same. The Boy's surface can be cut into three mutually congruent
Congruence (geometry)
In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
pieces.
Model at Oberwolfach
The Mathematical Research Institute of OberwolfachMathematical Research Institute of Oberwolfach
The Mathematical Research Institute of Oberwolfach in Oberwolfach, Germany, was founded by mathematician Wilhelm Süss in 1944...
has a large model of a Boy's surface outside the entrance, constructed and donated by Mercedes-Benz
Mercedes-Benz
Mercedes-Benz is a German manufacturer of automobiles, buses, coaches, and trucks. Mercedes-Benz is a division of its parent company, Daimler AG...
in January 1991. This model has 3-fold rotational symmetry
Rotational symmetry
Generally speaking, an object with rotational symmetry is an object that looks the same after a certain amount of rotation. An object may have more than one rotational symmetry; for instance, if reflections or turning it over are not counted, the triskelion appearing on the Isle of Man's flag has...
and minimizes the Willmore energy
Willmore energy
In differential geometry, the Willmore energy is a quantitative measure of how much a given surface deviates from a round sphere. Mathematically, the Willmore energy of a smooth closed surface embedded in three-dimensional Euclidean space is defined to be the integral of the mean curvature squared...
of the surface. It consists of steel strips which represent the image of a polar coordinate grid
Polar coordinate system
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a fixed point and an angle from a fixed direction....
under a parameterization given by Robert Bryant and Rob Kusner. The meridians (rays) become ordinary Möbius strip
Möbius strip
The Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...
s, i.e. twisted by 180 degrees. All but one of the strips corresponding to circles of latitude (radial circles around the origin) are untwisted, while the one corresponding to the boundary of the unit circle is a Möbius strip twisted by three times 180 degrees — as is the emblem of the institute .
Applications
Boy's surface can be used in sphere eversion, as a half-way model. A half-way model is an immersion of the sphere with the property that a rotation interchanges inside and outside, and so can be employed to evert (turn inside-out) a sphere. Boy's (the case p = 3) and Morin's (the case p = 2) surfaces are beginning of a sequence of half-way models with higher symmetry first proposed by George Francis, indexed by the even integers 2p (for p odd, these immersions can be factor through a projective plane). Kusner's parametrization yields all these.Parametrization of Boy's surface
Boy's surface can be parametrized in several ways. One parametrization, discovered by Rob Kusner and Robert BryantRobert Bryant
Robert Bryant is an American mathematician specializing in differential geometry. As of 2007, he has served as the chairman of the Mathematical Sciences Research Institute . He is known for his work in exterior differential systems, special holonomy, and Finsler geometry. He is also a senior...
, is the following: given a complex number z whose magnitude
Magnitude (mathematics)
The magnitude of an object in mathematics is its size: a property by which it can be compared as larger or smaller than other objects of the same kind; in technical terms, an ordering of the class of objects to which it belongs....
is less than or equal to one (
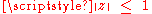), let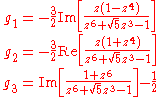so that
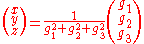
where x, y, and z are the desired Cartesian coordinates of a point on the Boy's surface.
If one performs an inversion of this parametrization centered on the triple point, one obtains a complete minimal surface
Minimal surface
In mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....
with three "ends" (that's how this parametrization was discovered naturally). This implies that the Bryant-Kusner parametrization of Boy's surfaces is "optimal" in the sense that it is the "least bent" immersion of a projective plane into three-space.
Property of Bryant-Kusner parametrization
If z is replaced by the negative reciprocal of its complex conjugateComplex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
,
then the functions g1, g2, and g3 of z are left unchanged.Relating the Boy's surface to the real projective plane
Let, where denote a pointPoint (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
on Boy's surface. Then
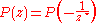
but only if
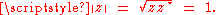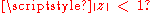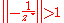
What if Thenbecause
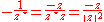
whose magnitude is
but
so thatSince P(z) belongs to the Boy's surface only when
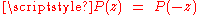, this means that belongs to Boy's surface only if Thus if but all other points on the Boy's surface are unique. The set of complex values is the unit disk, Thus the Boy's surface has been parametrized by a disk such that pairs of diametrically opposite points on the perimeterPerimeter
A perimeter is a path that surrounds an area. The word comes from the Greek peri and meter . The term may be used either for the path or its length - it can be thought of as the length of the outline of a shape. The perimeter of a circular area is called circumference.- Practical uses :Calculating...
of the disk are equivalent. Therefore the Boy's surface is homeomorphic
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
to the real projective plane
Real projective plane
In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
, RP2.
External links
- A planar unfolding of the Boy's surface - applet from Plus Magazine.
- Boy's surface resources, including the original article, and an embedding of a topologist in the Oberwolfach Boy's surface.
- A paper model of Boy's surface - pattern and instructions
- The Boy's surface implemented in interlocking plastic toy bricks
- Java-based model that can be freely rotated
- Line field coloring using Boy's surface
