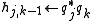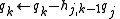Arnoldi iteration
Encyclopedia
In numerical
linear algebra
, the Arnoldi iteration is an eigenvalue algorithm
and an important example of iterative method
s. Arnoldi finds the eigenvalues of general (possibly non-Hermitian) matrices
; an analogous method for Hermitian matrices is the Lanczos iteration
. The Arnoldi iteration was invented by W. E. Arnoldi in 1951.
The term iterative method, used to describe Arnoldi, can perhaps be somewhat confusing. Note that all general eigenvalue algorithms must be iterative. This is not what is referred to when we say Arnoldi is an iterative method. Rather, Arnoldi belongs to a class of linear algebra algorithm
s (based on the idea of Krylov subspace
s) that give a partial result after a relatively small number of iterations. This is in contrast to so-called direct methods, which must complete to give any useful results.
Arnoldi iteration is a typical large sparse matrix algorithm: It does not access the elements of the matrix directly, but rather makes the matrix map vectors and makes its conclusions from their images. This is the motivation for building the Krylov subspace
.
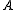 is the power iteration
is the power iteration
. Starting with an initial random vector
b, this method calculates Ab, A2b, A3b,… iteratively storing and normalizing the result into b on every turn. This sequence converges to the eigenvector corresponding to the largest eigenvalue,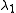 . However, much potentially useful computation is wasted by using only the final result,
. However, much potentially useful computation is wasted by using only the final result, 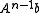 . This suggests that instead, we form the so-called Krylov matrix:
. This suggests that instead, we form the so-called Krylov matrix: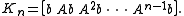
The columns of this matrix are not orthogonal, but in principle, we can extract an orthogonal basis
, via a method such as Gram–Schmidt orthogonalization
. The resulting vectors are a basis of the Krylov subspace
,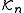 . We may expect the vectors of this basis to give good approximations of the eigenvectors corresponding to the
. We may expect the vectors of this basis to give good approximations of the eigenvectors corresponding to the  largest eigenvalues, for the same reason that
largest eigenvalues, for the same reason that 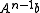 approximates the dominant eigenvector.
approximates the dominant eigenvector.
. This is where the Arnoldi iteration enters.
The Arnoldi iteration uses the stabilized Gram–Schmidt process
to produce a sequence of orthonormal vectors, q1, q2, q3, …, called the Arnoldi vectors, such that for every n, the vectors q1, …, qn span the Krylov subspace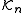 . Explicitly, the algorithm is as follows:
. Explicitly, the algorithm is as follows:
The j-loop projects out the component of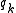 in the directions of
in the directions of 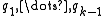 . This ensures the orthogonality of all the generated vectors.
. This ensures the orthogonality of all the generated vectors.
The algorithm breaks down when qk is the zero vector. This happens when the minimal polynomial of A is of degree k. In most applications of the Arnoldi iteration, including the eigenvalue algorithm below and GMRES, the algorithm has converged at this point.
Every step of the k-loop takes one matrix-vector product and approximately 4mk floating point operations.
) matrix formed by the numbers hj,k computed by the algorithm: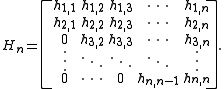
We then have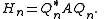
This yields an alternative interpretation of the Arnoldi iteration as a (partial) orthogonal reduction of A to Hessenberg form. The matrix Hn can be viewed as the representation in the basis formed by the Arnoldi vectors of the orthogonal projection of A onto the Krylov subspace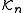 .
.
The matrix Hn can be characterized by the following optimality condition. The characteristic polynomial
of Hn minimizes ||p(A)q1||2 among all monic polynomials of degree n (the word monic means that the leading coefficient is 1). This optimality problem has a unique solution if and only if the Arnoldi iteration does not break down.
The relation between the Q matrices in subsequent iterations is given by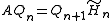
where
is an (n+1)-by-n matrix formed by adding an extra row to Hn.
is to compute the eigenvalues of the orthogonal projection of A onto the Krylov subspace. This projection is represented by Hn. The eigenvalues of Hn are called the Ritz eigenvalues. Since Hn is a Hessenberg matrix of modest size, its eigenvalues can be computed efficiently, for instance with the QR algorithm
.
It is often observed in practice that some of the Ritz eigenvalues converge to eigenvalues of A. Since Hn is n-by-n, it has at most n eigenvalues, and not all eigenvalues of A can be approximated. Typically, the Ritz eigenvalues converge to the extreme eigenvalues of A. This can be related to the characterization of Hn as the matrix whose characteristic polynomial minimizes ||p(A)q1|| in the following way. A good way to get p(A) small is to choose the polynomial p such that p(x) is small whenever x is an eigenvalue of A. Hence, the zeros of p (and thus the Ritz eigenvalues) will be close to the eigenvalues of A.
However, the details are not fully understood yet. This is in contrast to the case where A is symmetric. In that situation, the Arnoldi iteration becomes the Lanczos iteration
, for which the theory is more complete.
. This has spurred a number of other variations including Implicitly Restarted Lanczos method. It also influenced how other restarted methods are analyzed.
Theoretical results have shown that convergence improves with an increase in the Krylov subspace dimension n. However, an a-priori value of n which would lead to optimal convergence is not known. Recently a dynamic switching strategy has been proposed which fluctuates the dimension n before each restarts and thus leads to acceleration in the rate of convergence.
(GMRES) is a method for solving Ax = b based on Arnoldi iteration.
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, the Arnoldi iteration is an eigenvalue algorithm
Eigenvalue algorithm
In linear algebra, one of the most important problems is designing efficient and stable algorithms for finding the eigenvalues of a matrix. These eigenvalue algorithms may also find eigenvectors.-Characteristic polynomial:...
and an important example of iterative method
Iterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
s. Arnoldi finds the eigenvalues of general (possibly non-Hermitian) matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
; an analogous method for Hermitian matrices is the Lanczos iteration
Lanczos algorithm
The Lanczos algorithm is an iterative algorithm invented by Cornelius Lanczos that is an adaptation of power methods to find eigenvalues and eigenvectors of a square matrix or the singular value decomposition of a rectangular matrix. It is particularly useful for finding decompositions of very...
. The Arnoldi iteration was invented by W. E. Arnoldi in 1951.
The term iterative method, used to describe Arnoldi, can perhaps be somewhat confusing. Note that all general eigenvalue algorithms must be iterative. This is not what is referred to when we say Arnoldi is an iterative method. Rather, Arnoldi belongs to a class of linear algebra algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s (based on the idea of Krylov subspace
Krylov subspace
In linear algebra, the order-r Krylov subspace generated by an n-by-n matrix A and a vector b of dimension n is the linear subspace spanned by the images of b under the first r powers of A , that is,...
s) that give a partial result after a relatively small number of iterations. This is in contrast to so-called direct methods, which must complete to give any useful results.
Arnoldi iteration is a typical large sparse matrix algorithm: It does not access the elements of the matrix directly, but rather makes the matrix map vectors and makes its conclusions from their images. This is the motivation for building the Krylov subspace
Krylov subspace
In linear algebra, the order-r Krylov subspace generated by an n-by-n matrix A and a vector b of dimension n is the linear subspace spanned by the images of b under the first r powers of A , that is,...
.
Krylov subspaces and the power iteration
An intuitive method for finding an eigenvalue (specifically the largest eigenvalue) of a given m × m matrix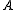 is the power iteration
is the power iterationPower iteration
In mathematics, the power iteration is an eigenvalue algorithm: given a matrix A, the algorithm will produce a number λ and a nonzero vector v , such that Av = λv....
. Starting with an initial random vector
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
b, this method calculates Ab, A2b, A3b,… iteratively storing and normalizing the result into b on every turn. This sequence converges to the eigenvector corresponding to the largest eigenvalue,
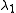 . However, much potentially useful computation is wasted by using only the final result,
. However, much potentially useful computation is wasted by using only the final result, 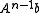 . This suggests that instead, we form the so-called Krylov matrix:
. This suggests that instead, we form the so-called Krylov matrix: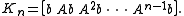
The columns of this matrix are not orthogonal, but in principle, we can extract an orthogonal basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
, via a method such as Gram–Schmidt orthogonalization
Gram–Schmidt process
In mathematics, particularly linear algebra and numerical analysis, the Gram–Schmidt process is a method for orthonormalising a set of vectors in an inner product space, most commonly the Euclidean space Rn...
. The resulting vectors are a basis of the Krylov subspace
Krylov subspace
In linear algebra, the order-r Krylov subspace generated by an n-by-n matrix A and a vector b of dimension n is the linear subspace spanned by the images of b under the first r powers of A , that is,...
,
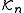 . We may expect the vectors of this basis to give good approximations of the eigenvectors corresponding to the
. We may expect the vectors of this basis to give good approximations of the eigenvectors corresponding to the  largest eigenvalues, for the same reason that
largest eigenvalues, for the same reason that 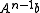 approximates the dominant eigenvector.
approximates the dominant eigenvector.The Arnoldi iteration
The process described above is intuitive. Unfortunately, it is also unstableNumerical stability
In the mathematical subfield of numerical analysis, numerical stability is a desirable property of numerical algorithms. The precise definition of stability depends on the context, but it is related to the accuracy of the algorithm....
. This is where the Arnoldi iteration enters.
The Arnoldi iteration uses the stabilized Gram–Schmidt process
Gram–Schmidt process
In mathematics, particularly linear algebra and numerical analysis, the Gram–Schmidt process is a method for orthonormalising a set of vectors in an inner product space, most commonly the Euclidean space Rn...
to produce a sequence of orthonormal vectors, q1, q2, q3, …, called the Arnoldi vectors, such that for every n, the vectors q1, …, qn span the Krylov subspace
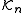 . Explicitly, the algorithm is as follows:
. Explicitly, the algorithm is as follows:- Start with an arbitrary vector q1 with norm 1.
- Repeat for k = 2, 3, …
-
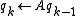
- for j from 1 to k − 1
-
-
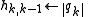
-
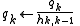
-
The j-loop projects out the component of
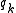 in the directions of
in the directions of 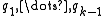 . This ensures the orthogonality of all the generated vectors.
. This ensures the orthogonality of all the generated vectors.The algorithm breaks down when qk is the zero vector. This happens when the minimal polynomial of A is of degree k. In most applications of the Arnoldi iteration, including the eigenvalue algorithm below and GMRES, the algorithm has converged at this point.
Every step of the k-loop takes one matrix-vector product and approximately 4mk floating point operations.
Properties of the Arnoldi iteration
Let Qn denote the m-by-n matrix formed by the first n Arnoldi vectors q1, q2, …, qn, and let Hn be the (upper HessenbergHessenberg matrix
In linear algebra, a Hessenberg matrix is a special kind of square matrix, one that is "almost" triangular. To be exact, an upper Hessenberg matrix has zero entries below the first subdiagonal, and a lower Hessenberg matrix has zero entries above the first superdiagonal...
) matrix formed by the numbers hj,k computed by the algorithm:
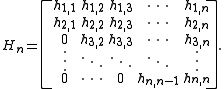
We then have
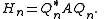
This yields an alternative interpretation of the Arnoldi iteration as a (partial) orthogonal reduction of A to Hessenberg form. The matrix Hn can be viewed as the representation in the basis formed by the Arnoldi vectors of the orthogonal projection of A onto the Krylov subspace
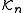 .
.The matrix Hn can be characterized by the following optimality condition. The characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of Hn minimizes ||p(A)q1||2 among all monic polynomials of degree n (the word monic means that the leading coefficient is 1). This optimality problem has a unique solution if and only if the Arnoldi iteration does not break down.
The relation between the Q matrices in subsequent iterations is given by
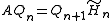
where

is an (n+1)-by-n matrix formed by adding an extra row to Hn.
Finding eigenvalues with the Arnoldi iteration
The idea of the Arnoldi iteration as an eigenvalue algorithmEigenvalue algorithm
In linear algebra, one of the most important problems is designing efficient and stable algorithms for finding the eigenvalues of a matrix. These eigenvalue algorithms may also find eigenvectors.-Characteristic polynomial:...
is to compute the eigenvalues of the orthogonal projection of A onto the Krylov subspace. This projection is represented by Hn. The eigenvalues of Hn are called the Ritz eigenvalues. Since Hn is a Hessenberg matrix of modest size, its eigenvalues can be computed efficiently, for instance with the QR algorithm
QR algorithm
In numerical linear algebra, the QR algorithm is an eigenvalue algorithm: that is, a procedure to calculate the eigenvalues and eigenvectors of a matrix. The QR transformation was developed in the late 1950s by John G.F. Francis and by Vera N. Kublanovskaya , working independently...
.
It is often observed in practice that some of the Ritz eigenvalues converge to eigenvalues of A. Since Hn is n-by-n, it has at most n eigenvalues, and not all eigenvalues of A can be approximated. Typically, the Ritz eigenvalues converge to the extreme eigenvalues of A. This can be related to the characterization of Hn as the matrix whose characteristic polynomial minimizes ||p(A)q1|| in the following way. A good way to get p(A) small is to choose the polynomial p such that p(x) is small whenever x is an eigenvalue of A. Hence, the zeros of p (and thus the Ritz eigenvalues) will be close to the eigenvalues of A.
However, the details are not fully understood yet. This is in contrast to the case where A is symmetric. In that situation, the Arnoldi iteration becomes the Lanczos iteration
Lanczos algorithm
The Lanczos algorithm is an iterative algorithm invented by Cornelius Lanczos that is an adaptation of power methods to find eigenvalues and eigenvectors of a square matrix or the singular value decomposition of a rectangular matrix. It is particularly useful for finding decompositions of very...
, for which the theory is more complete.
Implicitly restarted Arnoldi method (IRAM)
Due to practical storage consideration, common implementations of Arnoldi methods typically restart after some number of iterations. One major innovation in restarting was due to Lehoucq and Sorensen who proposed the Implicitly Restarted Arnoldi Method. They also implemented the algorithm in a freely available software package called ARPACKARPACK
ARPACK, the ARnoldi PACKage, is a numericalsoftware library written in FORTRAN 77 for solving large scale eigenvalue problems.The package is designed to compute a few eigenvalues and corresponding...
. This has spurred a number of other variations including Implicitly Restarted Lanczos method. It also influenced how other restarted methods are analyzed.
Theoretical results have shown that convergence improves with an increase in the Krylov subspace dimension n. However, an a-priori value of n which would lead to optimal convergence is not known. Recently a dynamic switching strategy has been proposed which fluctuates the dimension n before each restarts and thus leads to acceleration in the rate of convergence.
See also
The generalized minimal residual methodGeneralized minimal residual method
In mathematics, the generalized minimal residual method is an iterative method for the numerical solution of a system of linear equations. The method approximates the solution by the vector in a Krylov subspace with minimal residual. The Arnoldi iteration is used to find this vector.The GMRES...
(GMRES) is a method for solving Ax = b based on Arnoldi iteration.