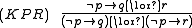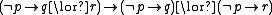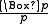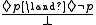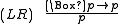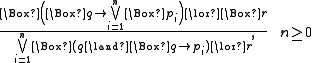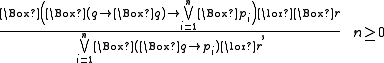Admissible rule
Encyclopedia
In logic
, a rule of inference
is admissible in a formal system
if the set of theorems of the system does not change when that rule is added to the existing rules of the system. In other words, every formula that can be derived using that rule is already derivable without that rule, so, in a sense, it is redundant. The concept of an admissible rule was introduced by Paul Lorenzen
(1955).
s, which we will describe next.
Let a set of basic propositional connective
s be fixed (for instance,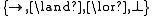 in the case of superintuitionistic logics, or
in the case of superintuitionistic logics, or 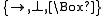 in the case of monomodal logic
in the case of monomodal logic
s). Well-formed formulas are built freely using these connectives from a countably infinite
set of propositional variable
s pn. A substitution
σ is a function from formulas to formulas which commutes with the connectives, i.e.,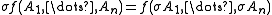
for every connective f, and formulas A1, …, An. (We may also apply substitutions to sets Γ of formulas, making ) A Tarski-style consequence relation is a relation between sets of formulas, and formulas, such that
between sets of formulas, and formulas, such that
for all formulas A, B, and sets of formulas Γ, Δ. A consequence relation such that
for all substitutions σ is called structural. (Note that the term "structural" as used here and below is unrelated to the notion of structural rule
s in sequent calculi
.) A structural consequence relation is called a propositional logic. A formula A is a theorem
of a logic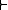 if
if 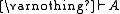 .
.
For example, we identify a superintuitionistic logic L with its standard consequence relation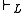 axiomatizable by modus ponens
axiomatizable by modus ponens
and axioms, and we identify a normal modal logic
with its global consequence relation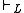 axiomatized by modus ponens, necessitation, and axioms.
axiomatized by modus ponens, necessitation, and axioms.
A structural inference rule (or just rule for short) is given by a pair (Γ,B), usually written as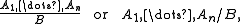
where Γ = {A1, …, An} is a finite set of formulas, and B is a formula. An instance of the rule is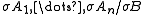
for a substitution σ. The rule Γ/B is derivable in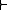 , if
, if  . It is admissible if for every instance of the rule, σB is a theorem whenever all formulas from σΓ are theorems. In other words, a rule is admissible if, when added to the logic, does not lead to new theorems. We also write
. It is admissible if for every instance of the rule, σB is a theorem whenever all formulas from σΓ are theorems. In other words, a rule is admissible if, when added to the logic, does not lead to new theorems. We also write 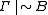 if Γ/B is admissible. (Note that
if Γ/B is admissible. (Note that 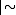 is a structural consequence relation on its own.)
is a structural consequence relation on its own.)
Every derivable rule is admissible, but not vice versa in general. A logic is structurally complete if every admissible rule is derivable, i.e.,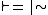 .
.
In logics with a well-behaved conjunction
connective (such as superintuitionistic or modal logics), a rule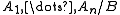 is equivalent to
is equivalent to 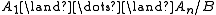 with respect to admissibility and derivability. It is therefore customary to only deal with unary
with respect to admissibility and derivability. It is therefore customary to only deal with unary
rules A/B.
: the definition of admissibility of a rule A/B involves an unbounded universal quantifier over all propositional substitutions, hence a priori we only now that admissibility of rule in a decidable logic is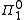 (i.e., its complement is recursively enumerable). For instance, it is known that admissibility in the bimodal logics Ku and K4u (the extensions of K or K4 with the universal modality) is undecidable. Remarkably, decidability of admissibility in the basic modal logic K is a major open problem.
(i.e., its complement is recursively enumerable). For instance, it is known that admissibility in the bimodal logics Ku and K4u (the extensions of K or K4 with the universal modality) is undecidable. Remarkably, decidability of admissibility in the basic modal logic K is a major open problem.
Nevertheless, admissibility of rules is known to be decidable in many modal and superintuitionistic logics. The first decision procedures for admissible rules in basic transitive modal logics were constructed by Rybakov, using the reduced form of rules. A modal rule in variables p0, …, pk is called reduced if it has the form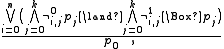
where each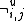 is either blank, or negation
is either blank, or negation  . For each rule r, we can effectively construct a reduced rule s (called the reduced form of r) such that any logic admits (or derives) r if and only if it admits (or derives) s, by introducing extension variables for all subformulas in A, and expressing the result in the full disjunctive normal form
. For each rule r, we can effectively construct a reduced rule s (called the reduced form of r) such that any logic admits (or derives) r if and only if it admits (or derives) s, by introducing extension variables for all subformulas in A, and expressing the result in the full disjunctive normal form
. It is thus sufficient to construct a decision algorithm for admissibility of reduced rules.
Let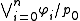 be a reduced rule as above. We identify every conjunction
be a reduced rule as above. We identify every conjunction 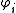 with the set
with the set 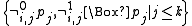 of its conjuncts. For any subset W of the set
of its conjuncts. For any subset W of the set 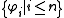 of all conjunctions, let us define a Kripke model
of all conjunctions, let us define a Kripke model 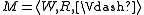 by
by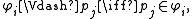
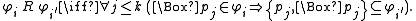
Then the following provides an algorithmic criterion for admissibility in K4:
Theorem. The rule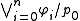 is not admissible in K4 if and only if there exists a set
is not admissible in K4 if and only if there exists a set 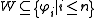 such that
such that
Similar criteria can be found for the logics S4, GL, and Grz. Furthermore, admissibility in intuitionistic logic can be reduced to admissibility in Grz using the Gödel–McKinsey–Tarski translation
: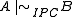 if and only if
if and only if 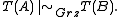
Rybakov (1997) developed much more sophisticated techniques for showing decidability of admissibility, which apply to a robust (infinite) class of transitive (i.e., extending K4 or IPC) modal and superintuitionistic logics, including e.g. S4.1, S4.2, S4.3, KC, Tk (as well as the above mentioned logics IPC, K4, S4, GL, Grz).
Despite being decidable, the admissibility problem has relatively high computational complexity
, even in simple logics: admissibility of rules in the basic transitive logics IPC, K4, S4, GL, Grz is coNEXP-complete. This should be contrasted with the derivability problem (for rules or formulas) in these logics, which is PSPACE
-complete.
in the equational theory of modal
or Heyting algebra
s. The connection was developed by Ghilardi (1999, 2000). In the logical setup, a unifier of a formula A in a logic L (an L-unifier for short) is a substitution σ such that σA is a theorem of L. (Using this notion, we can rephrase admissibility of a rule A/B in L as "every L-unifier of A is an L-unifier of B".) An L-unifier σ is less general than an L-unifier τ, written as σ ≤ τ, if there exists a substitution υ such that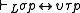
for every variable p. A complete set of unifiers of a formula A is a set S of L-unifiers of A such that every L-unifier of A is less general than some unifier from S. A most general unifier (mgu) of A is a unifier σ such that {σ} is a complete set of unifiers of A. It follows that if S is a complete set of unifiers of A, then a rule A/B is L-admissible if and only if every σ in S is an L-unifier of B. Thus we can characterize admissible rules if we can find well-behaved complete sets of unifiers.
An important class of formulas which have a most general unifier are the projective formulas: these are formulas A such that there exists a unifier σ of A such that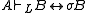
for every formula B. Note that σ is a mgu of A. In transitive modal and superintuitionistic logics with the finite model property (fmp), one can characterize projective formulas semantically as those whose set of finite L-models has the extension property: if M is a finite Kripke L-model with a root r whose cluster is a singleton, and the formula A holds in all points of M except for r, then we can change the valuation of variables in r so as to make A true in r as well. Moreover, the proof provides an explicit construction of a mgu for a given projective formula A.
In the basic transitive logics IPC, K4, S4, GL, Grz (and more generally in any transitive logic with the fmp whose set of finite frame satisfies another kind of extension property), we can effectively construct for any formula A its projective approximation Π(A): a finite set of projective formulas such that
It follows that the set of mgus of elements of Π(A) is a complete set of unifiers of A. Furthermore, if P is a projective formula, then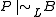 if and only if
if and only if 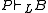
for any formula B. Thus we obtain the following effective characterization of admissible rules: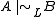 if and only if
if and only if 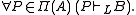
of admissible rules, if every admissible rule Γ/B can be derived from R and the derivable rules of L, using substitution, composition, and weakening. In other words, R is a basis if and only if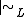 is the smallest structural consequence relation which includes
is the smallest structural consequence relation which includes 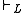 and R.
and R.
Notice that decidability of admissible rules of a decidable logic is equivalent to the existence of recursive (or recursively enumerable) bases: on the one hand, the set of all admissible rule is a recursive basis if admissibility is decidable. On the other hand, the set of admissible rules is always co-r.e., and if we further have an r.e. basis, it is also r.e., hence it is decidable. (In other words, we can decide admissibility of A/B by the following algorithm
: we start in parallel two exhaustive searches, one for a substitution σ which unifies A but not B, and one for a derivation of A/B from R and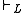 . One of the searches has to eventually come up with an answer.) Apart from decidability, explicit bases of admissible rules are useful for some applications, e.g. in proof complexity
. One of the searches has to eventually come up with an answer.) Apart from decidability, explicit bases of admissible rules are useful for some applications, e.g. in proof complexity
.
For a given logic, we can ask whether it has a recursive or finite basis of admissible rules, and to provide an explicit basis. If a logic has no finite basis, it can nevertheless has an independent basis: a basis R such that no proper subset of R is a basis.
In general, very little can be said about existence of bases with desirable properties. For example, while tabular logics are generally well-behaved, and always finitely axiomatizable, there exist tabular modal logics without a finite or independent basis of rules. Finite bases are relatively rare: even the basic transitive logics IPC, K4, S4, GL, Grz do not have a finite basis of admissible rules, though they have independent bases.
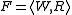 , if the following is true for every valuation
, if the following is true for every valuation 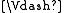 in F:
in F:
(The definition readily generalizes to general frame
s, if needed.)
Let X be a subset of W, and t a point in W. We say that t is
We say that a frame F has reflexive (irreflexive) tight predecessors, if for every finite subset X of W, there exists a reflexive (irreflexive) tight predecessor of X in W.
We have:
Note that apart from a few trivial cases, frames with tight predecessors must be infinite, hence admissible rules in basic transitive logics do not enjoy the finite model property.
Intuitionistic logic itself is not structurally complete, but its fragments may behave differently. Namely, any disjunction-free rule or implication-free rule admissible in a superintuitionistic logic is derivable. On the other hand, the Mints rule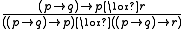
is admissible in intuitionistic logic but not derivable, and contains only implications and disjunctions.
We know the maximal structurally incomplete transitive logics. A logic is called hereditarily structurally complete, if every its extension is structurally complete. For example, classical logic, as well as the logics LC and Grz.3 mentioned above, are hereditarily structurally complete. A complete description of hereditarily structurally complete superintuitionistic and transitive modal logics was given by Citkin and Rybakov. Namely, a superintuitionistic logic is hereditarily structurally complete if and only if it is not valid in any of the five Kripke frames
Similarly, an extension of K4 is hereditarily structurally complete if and only if it is not valid in any of certain twenty Kripke frames (including the five intuitionistic frames above).
There exist structurally complete logics that are not hereditarily structurally complete: for example, Medvedev's logic
is structurally complete, but it is included in the structurally incomplete logic KC.
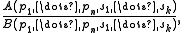
whose variables are divided into the "regular" variables pi, and the parameters si. The rule is L-admissible if every L-unifier σ of A such that σsi = si for each i is also a unifier of B. The basic decidability results for admissible rules also carry to rules with parameters.
A multiple-conclusion rule is a pair (Γ,Δ) of two finite sets of formulas, written as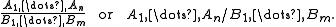
Such a rule is admissible if every unifier of Γ is also a unifier of some formula from Δ. For example, a logic L is consistent iff it admits the rule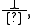
and a superintuitionistic logic has the disjunction property iff it admits the rule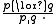
Again, basic results on admissible rules generalize smoothly to multiple-conclusion rules. In logics with a variant of the disjunction property, the multiple-conclusion rules have the same expressive power as single-conclusion rules: for example, in S4 the rule above is equivalent to
Nevertheless, multiple-conclusion rules can often be employed to simplify arguments.
In proof theory
, admissibility is often considered in the context of sequent calculi
, where the basic objects are sequents rather than formulas. For example, one can rephrase the cut-elimination theorem
as saying that the cut-free sequent calculus admits the cut rule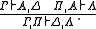
(By abuse of language, it is also sometimes said that the (full) sequent calculus admits cut, meaning its cut-free version does.) However, admissibility in sequent calculi is usually only a notational variant for admissibility in the corresponding logic: any complete calculus for (say) intuitionistic logic admits a sequent rule if and only if IPC admits the formula rule which we obtain by translating each sequent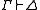 to its characteristic formula
to its characteristic formula 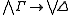 .
.
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, a rule of inference
Rule of inference
In logic, a rule of inference, inference rule, or transformation rule is the act of drawing a conclusion based on the form of premises interpreted as a function which takes premises, analyses their syntax, and returns a conclusion...
is admissible in a formal system
Formal system
In formal logic, a formal system consists of a formal language and a set of inference rules, used to derive an expression from one or more other premises that are antecedently supposed or derived . The axioms and rules may be called a deductive apparatus...
if the set of theorems of the system does not change when that rule is added to the existing rules of the system. In other words, every formula that can be derived using that rule is already derivable without that rule, so, in a sense, it is redundant. The concept of an admissible rule was introduced by Paul Lorenzen
Paul Lorenzen
Paul Lorenzen was a philosopher andmathematician.As a founder of the Erlangen School and the inventor of game semantics he was a famous German philosopher of the 20th century.-Biography:Lorenzen studied with David Hilbert as a schoolboy and he was one of Hasse's...
(1955).
Definitions
Admissibility has been systematically studied only in the case of structural rules in propositional non-classical logicNon-classical logic
Non-classical logics is the name given to formal systems which differ in a significant way from standard logical systems such as propositional and predicate logic. There are several ways in which this is done, including by way of extensions, deviations, and variations...
s, which we will describe next.
Let a set of basic propositional connective
Logical connective
In logic, a logical connective is a symbol or word used to connect two or more sentences in a grammatically valid way, such that the compound sentence produced has a truth value dependent on the respective truth values of the original sentences.Each logical connective can be expressed as a...
s be fixed (for instance,
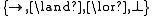 in the case of superintuitionistic logics, or
in the case of superintuitionistic logics, or 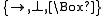 in the case of monomodal logic
in the case of monomodal logicModal logic
Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
s). Well-formed formulas are built freely using these connectives from a countably infinite
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
set of propositional variable
Propositional variable
In mathematical logic, a propositional variable is a variable which can either be true or false...
s pn. A substitution
Substitution (logic)
Substitution is a fundamental concept in logic. Substitution is a syntactic transformation on strings of symbols of a formal language.In propositional logic, a substitution instance of a propositional formula is a second formula obtained by replacing symbols of the original formula by other formulas...
σ is a function from formulas to formulas which commutes with the connectives, i.e.,
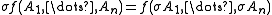
for every connective f, and formulas A1, …, An. (We may also apply substitutions to sets Γ of formulas, making ) A Tarski-style consequence relation is a relation
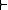 between sets of formulas, and formulas, such that
between sets of formulas, and formulas, such that
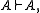
- if
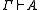 then
then 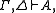
- if
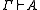 and
and 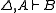 then
then 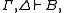
for all formulas A, B, and sets of formulas Γ, Δ. A consequence relation such that
- if
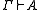 then
then 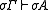
for all substitutions σ is called structural. (Note that the term "structural" as used here and below is unrelated to the notion of structural rule
Structural rule
In proof theory, a structural rule is an inference rule that does not refer to any logical connective, but instead operates on the judgements or sequents directly. Structural rules often mimic intended meta-theoretic properties of the logic...
s in sequent calculi
Sequent calculus
In proof theory and mathematical logic, sequent calculus is a family of formal systems sharing a certain style of inference and certain formal properties. The first sequent calculi, systems LK and LJ, were introduced by Gerhard Gentzen in 1934 as a tool for studying natural deduction in...
.) A structural consequence relation is called a propositional logic. A formula A is a theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
of a logic
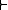 if
if 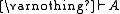 .
.For example, we identify a superintuitionistic logic L with its standard consequence relation
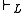 axiomatizable by modus ponens
axiomatizable by modus ponensModus ponens
In classical logic, modus ponendo ponens or implication elimination is a valid, simple argument form. It is related to another valid form of argument, modus tollens. Both Modus Ponens and Modus Tollens can be mistakenly used when proving arguments...
and axioms, and we identify a normal modal logic
Normal modal logic
In logic, a normal modal logic is a set L of modal formulas such that L contains:* All propositional tautologies;* All instances of the Kripke schema: \Box\toand it is closed under:...
with its global consequence relation
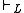 axiomatized by modus ponens, necessitation, and axioms.
axiomatized by modus ponens, necessitation, and axioms.A structural inference rule (or just rule for short) is given by a pair (Γ,B), usually written as
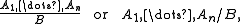
where Γ = {A1, …, An} is a finite set of formulas, and B is a formula. An instance of the rule is
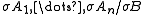
for a substitution σ. The rule Γ/B is derivable in
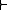 , if
, if 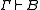 . It is admissible if for every instance of the rule, σB is a theorem whenever all formulas from σΓ are theorems. In other words, a rule is admissible if, when added to the logic, does not lead to new theorems. We also write
. It is admissible if for every instance of the rule, σB is a theorem whenever all formulas from σΓ are theorems. In other words, a rule is admissible if, when added to the logic, does not lead to new theorems. We also write 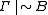 if Γ/B is admissible. (Note that
if Γ/B is admissible. (Note that 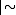 is a structural consequence relation on its own.)
is a structural consequence relation on its own.)Every derivable rule is admissible, but not vice versa in general. A logic is structurally complete if every admissible rule is derivable, i.e.,
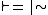 .
.In logics with a well-behaved conjunction
Logical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
connective (such as superintuitionistic or modal logics), a rule
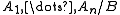 is equivalent to
is equivalent to 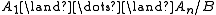 with respect to admissibility and derivability. It is therefore customary to only deal with unary
with respect to admissibility and derivability. It is therefore customary to only deal with unaryUnary operation
In mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
rules A/B.
Examples
- Classical propositional calculusClassical logicClassical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
(CPC) is structurally complete. Indeed, assume that A/B is non-derivable rule, and fix an assignment v such that v(A) = 1, and v(B) = 0. Define a substitution σ such that for every variable p, σp =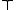 if v(p) = 1, and σp =
if v(p) = 1, and σp = 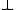 if v(p) = 0. Then σA is a theorem, but σB is not (in fact, ¬σB is a theorem). Thus the rule A/B is not admissible either. (The same argument applies to any multi-valued logicMulti-valued logicIn logic, a many-valued logic is a propositional calculus in which there are more than two truth values. Traditionally, in Aristotle's logical calculus, there were only two possible values for any proposition...
if v(p) = 0. Then σA is a theorem, but σB is not (in fact, ¬σB is a theorem). Thus the rule A/B is not admissible either. (The same argument applies to any multi-valued logicMulti-valued logicIn logic, a many-valued logic is a propositional calculus in which there are more than two truth values. Traditionally, in Aristotle's logical calculus, there were only two possible values for any proposition...
L complete with respect to a logical matrix whose all elements have a name in the language of L.) - The KreiselGeorg KreiselGeorg Kreisel FRS is an Austrian-born mathematical logician who has studied and worked in Great Britain and America. Kreisel came from a Jewish background; his family sent him to England before the Anschluss, where he studied mathematics at Trinity College, Cambridge and then, during World War...
–PutnamHilary PutnamHilary Whitehall Putnam is an American philosopher, mathematician and computer scientist, who has been a central figure in analytic philosophy since the 1960s, especially in philosophy of mind, philosophy of language, philosophy of mathematics, and philosophy of science...
rule (aka Harrop's rule, or independence of premise rule)
-
- is admissible in the intuitionistic propositional calculusIntuitionistic logicIntuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
(IPC). In fact, it is admissible in every superintuitionistic logic. On the other hand, the formula - is not an intuitionistic tautology, hence KPR is not derivable in IPC. In particular, IPC is not structurally complete.
- The rule
- is admissible in many modal logics, such as K, D, K4, S4, GL (see this table for names of modal logics). It is derivable in S4, but it is not derivable in K, D, K4, or GL.
- The rule
- is admissible in every normal modal logic. It is derivable in GL and S4.1, but it is not derivable in K, D, K4, S4, S5.
- Löb's ruleLöb's theoremIn mathematical logic, Löb's theorem states that in a theory with Peano arithmetic, for any formula P, if it is provable that "if P is provable then P", then P is provable...
- Löb's rule
- is admissible (but not derivable) in the basic modal logic K, and it is derivable in GL. However, LR is not admissible in K4. In particular, it is not true in general that a rule admissible in a logic L must be admissible in its extensions.
- The Gödel–Dummett logicIntermediate logicIn mathematical logic, a superintuitionistic logic is a propositional logic extending intuitionistic logic. Classical logic is the strongest consistent superintuitionistic logic, thus consistent superintuitionistic logics are called intermediate logics .-Definition:A superintuitionistic logic is a...
(LC), and the modal logic Grz.3 are structurally complete. The product fuzzy logicT-norm fuzzy logicsT-norm fuzzy logics are a family of non-classical logics, informally delimited by having a semantics which takes the real unit interval [0, 1] for the system of truth values and functions called t-norms for permissible interpretations of conjunction...
is also structurally complete.
- The Gödel–Dummett logic
Decidability and reduced rules
The basic question about admissible rules of a given logic is whether the set of all admissible rules is decidable. Note that the problem is nontrivial even if the logic itself (i.e., its set of theorems) is decidableDecidability (logic)
In logic, the term decidable refers to the decision problem, the question of the existence of an effective method for determining membership in a set of formulas. Logical systems such as propositional logic are decidable if membership in their set of logically valid formulas can be effectively...
: the definition of admissibility of a rule A/B involves an unbounded universal quantifier over all propositional substitutions, hence a priori we only now that admissibility of rule in a decidable logic is
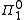 (i.e., its complement is recursively enumerable). For instance, it is known that admissibility in the bimodal logics Ku and K4u (the extensions of K or K4 with the universal modality) is undecidable. Remarkably, decidability of admissibility in the basic modal logic K is a major open problem.
(i.e., its complement is recursively enumerable). For instance, it is known that admissibility in the bimodal logics Ku and K4u (the extensions of K or K4 with the universal modality) is undecidable. Remarkably, decidability of admissibility in the basic modal logic K is a major open problem.Nevertheless, admissibility of rules is known to be decidable in many modal and superintuitionistic logics. The first decision procedures for admissible rules in basic transitive modal logics were constructed by Rybakov, using the reduced form of rules. A modal rule in variables p0, …, pk is called reduced if it has the form
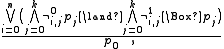
where each
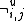 is either blank, or negation
is either blank, or negation  . For each rule r, we can effectively construct a reduced rule s (called the reduced form of r) such that any logic admits (or derives) r if and only if it admits (or derives) s, by introducing extension variables for all subformulas in A, and expressing the result in the full disjunctive normal form
. For each rule r, we can effectively construct a reduced rule s (called the reduced form of r) such that any logic admits (or derives) r if and only if it admits (or derives) s, by introducing extension variables for all subformulas in A, and expressing the result in the full disjunctive normal formDisjunctive normal form
In boolean logic, a disjunctive normal form is a standardization of a logical formula which is a disjunction of conjunctive clauses. As a normal form, it is useful in automated theorem proving. A logical formula is considered to be in DNF if and only if it is a disjunction of one or more...
. It is thus sufficient to construct a decision algorithm for admissibility of reduced rules.
Let
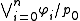 be a reduced rule as above. We identify every conjunction
be a reduced rule as above. We identify every conjunction 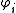 with the set
with the set 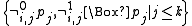 of its conjuncts. For any subset W of the set
of its conjuncts. For any subset W of the set 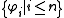 of all conjunctions, let us define a Kripke model
of all conjunctions, let us define a Kripke model 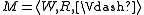 by
by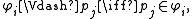
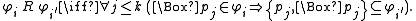
Then the following provides an algorithmic criterion for admissibility in K4:
Theorem. The rule
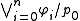 is not admissible in K4 if and only if there exists a set
is not admissible in K4 if and only if there exists a set 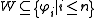 such that
such that
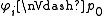 for some
for some 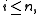
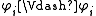 for every
for every 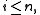
- for every subset D of W there exist elements
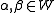 such that the equivalences
such that the equivalences
-
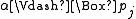 if and only if
if and only if 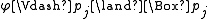 for every
for every 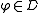
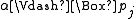 if and only if
if and only if 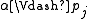 and
and 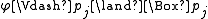 for every
for every 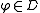
- hold for all j.
Similar criteria can be found for the logics S4, GL, and Grz. Furthermore, admissibility in intuitionistic logic can be reduced to admissibility in Grz using the Gödel–McKinsey–Tarski translation
Modal companion
In logic, a modal companion of a superintuitionistic logic L is a normal modal logic which interprets L by a certain canonical translation, described below...
:
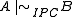 if and only if
if and only if 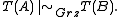
Rybakov (1997) developed much more sophisticated techniques for showing decidability of admissibility, which apply to a robust (infinite) class of transitive (i.e., extending K4 or IPC) modal and superintuitionistic logics, including e.g. S4.1, S4.2, S4.3, KC, Tk (as well as the above mentioned logics IPC, K4, S4, GL, Grz).
Despite being decidable, the admissibility problem has relatively high computational complexity
Computational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
, even in simple logics: admissibility of rules in the basic transitive logics IPC, K4, S4, GL, Grz is coNEXP-complete. This should be contrasted with the derivability problem (for rules or formulas) in these logics, which is PSPACE
PSPACE
In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :...
-complete.
Projectivity and unification
Admissibility in propositional logics is closely related to unificationUnification
Unification, in computer science and logic, is an algorithmic process by which one attempts to solve the satisfiability problem. The goal of unification is to find a substitution which demonstrates that two seemingly different terms are in fact either identical or just equal...
in the equational theory of modal
Modal algebra
In algebra and logic, a modal algebra is a structure \langle A,\land,\lor,-,0,1,\Box\rangle such that*\langle A,\land,\lor,-,0,1\rangle is a Boolean algebra,...
or Heyting algebra
Heyting algebra
In mathematics, a Heyting algebra, named after Arend Heyting, is a bounded lattice equipped with a binary operation a→b of implication such that ∧a ≤ b, and moreover a→b is the greatest such in the sense that if c∧a ≤ b then c ≤ a→b...
s. The connection was developed by Ghilardi (1999, 2000). In the logical setup, a unifier of a formula A in a logic L (an L-unifier for short) is a substitution σ such that σA is a theorem of L. (Using this notion, we can rephrase admissibility of a rule A/B in L as "every L-unifier of A is an L-unifier of B".) An L-unifier σ is less general than an L-unifier τ, written as σ ≤ τ, if there exists a substitution υ such that
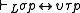
for every variable p. A complete set of unifiers of a formula A is a set S of L-unifiers of A such that every L-unifier of A is less general than some unifier from S. A most general unifier (mgu) of A is a unifier σ such that {σ} is a complete set of unifiers of A. It follows that if S is a complete set of unifiers of A, then a rule A/B is L-admissible if and only if every σ in S is an L-unifier of B. Thus we can characterize admissible rules if we can find well-behaved complete sets of unifiers.
An important class of formulas which have a most general unifier are the projective formulas: these are formulas A such that there exists a unifier σ of A such that
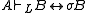
for every formula B. Note that σ is a mgu of A. In transitive modal and superintuitionistic logics with the finite model property (fmp), one can characterize projective formulas semantically as those whose set of finite L-models has the extension property: if M is a finite Kripke L-model with a root r whose cluster is a singleton, and the formula A holds in all points of M except for r, then we can change the valuation of variables in r so as to make A true in r as well. Moreover, the proof provides an explicit construction of a mgu for a given projective formula A.
In the basic transitive logics IPC, K4, S4, GL, Grz (and more generally in any transitive logic with the fmp whose set of finite frame satisfies another kind of extension property), we can effectively construct for any formula A its projective approximation Π(A): a finite set of projective formulas such that
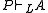 for every
for every 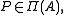
- every unifier of A is a unifier of a formula from Π(A).
It follows that the set of mgus of elements of Π(A) is a complete set of unifiers of A. Furthermore, if P is a projective formula, then
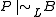 if and only if
if and only if 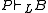
for any formula B. Thus we obtain the following effective characterization of admissible rules:
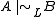 if and only if
if and only if 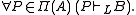
Bases of admissible rules
Let L be a logic. A set R of L-admissible rule is called a basisBasis
Basis may refer to* Cost basis, in income tax law, the original cost of property adjusted for factors such as depreciation.* Basis of futures, the value differential between a future and the spot price...
of admissible rules, if every admissible rule Γ/B can be derived from R and the derivable rules of L, using substitution, composition, and weakening. In other words, R is a basis if and only if
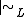 is the smallest structural consequence relation which includes
is the smallest structural consequence relation which includes 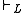 and R.
and R.Notice that decidability of admissible rules of a decidable logic is equivalent to the existence of recursive (or recursively enumerable) bases: on the one hand, the set of all admissible rule is a recursive basis if admissibility is decidable. On the other hand, the set of admissible rules is always co-r.e., and if we further have an r.e. basis, it is also r.e., hence it is decidable. (In other words, we can decide admissibility of A/B by the following algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
: we start in parallel two exhaustive searches, one for a substitution σ which unifies A but not B, and one for a derivation of A/B from R and
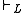 . One of the searches has to eventually come up with an answer.) Apart from decidability, explicit bases of admissible rules are useful for some applications, e.g. in proof complexity
. One of the searches has to eventually come up with an answer.) Apart from decidability, explicit bases of admissible rules are useful for some applications, e.g. in proof complexityProof complexity
In computer science, proof complexity is a measure of efficiency of automated theorem proving methods that is based on the size of the proofs they produce. The methods for proving contradiction in propositional logic are the most analyzed...
.
For a given logic, we can ask whether it has a recursive or finite basis of admissible rules, and to provide an explicit basis. If a logic has no finite basis, it can nevertheless has an independent basis: a basis R such that no proper subset of R is a basis.
In general, very little can be said about existence of bases with desirable properties. For example, while tabular logics are generally well-behaved, and always finitely axiomatizable, there exist tabular modal logics without a finite or independent basis of rules. Finite bases are relatively rare: even the basic transitive logics IPC, K4, S4, GL, Grz do not have a finite basis of admissible rules, though they have independent bases.
Examples of bases
- The empty set is a basis of L-admissible rules if and only if L is structurally complete.
- Every extension of the modal logic S4.3 (including, notably, S5) has a finite basis consisting of the single rule
-
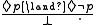
- Visser's rules
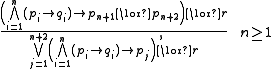
- are a basis of admissible rules in IPC or KC.
- The rules
- are a basis of admissible rules of GL. (Note that the empty disjunction is defined as
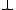 .)
.)
- The rules
- are a basis of admissible rules of S4 or Grz.
Semantics for admissible rules
A rule Γ/B is valid in a modal or intuitionistic Kripke frame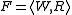 , if the following is true for every valuation
, if the following is true for every valuation 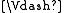 in F:
in F:
- if
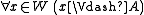 for all
for all 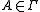 , then
, then 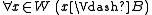 .
.
(The definition readily generalizes to general frame
General frame
In logic, general frames are Kripke frames with an additional structure, which are used to model modal and intermediate logics...
s, if needed.)
Let X be a subset of W, and t a point in W. We say that t is
- a reflexive tight predecessor of X, if for every y in W: t R y if and only if t = y or x = y or x R y for some x in X,
- an irreflexive tight predecessor of X, if for every y in W: t R y if and only if x = y or x R y for some x in X.
We say that a frame F has reflexive (irreflexive) tight predecessors, if for every finite subset X of W, there exists a reflexive (irreflexive) tight predecessor of X in W.
We have:
- a rule is admissible in IPC if and only if it is valid in all intuitionistic frames which have reflexive tight predecessors,
- a rule is admissible in K4 if and only if it is valid in all transitiveTransitive relationIn mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
frames which have reflexive and irreflexive tight predecessors, - a rule is admissible in S4 if and only if it is valid in all transitive reflexiveReflexive relationIn mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
frames which have reflexive tight predecessors, - a rule is admissible in GL if and only if it is valid in all transitive converse well-foundedWell-founded relationIn mathematics, a binary relation, R, is well-founded on a class X if and only if every non-empty subset of X has a minimal element with respect to R; that is, for every non-empty subset S of X, there is an element m of S such that for every element s of S, the pair is not in R:\forall S...
frames which have irreflexive tight predecessors.
Note that apart from a few trivial cases, frames with tight predecessors must be infinite, hence admissible rules in basic transitive logics do not enjoy the finite model property.
Structural completeness
While a general classification of structurally complete logics is not an easy task, we have a good understanding of some special cases.Intuitionistic logic itself is not structurally complete, but its fragments may behave differently. Namely, any disjunction-free rule or implication-free rule admissible in a superintuitionistic logic is derivable. On the other hand, the Mints rule
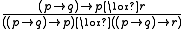
is admissible in intuitionistic logic but not derivable, and contains only implications and disjunctions.
We know the maximal structurally incomplete transitive logics. A logic is called hereditarily structurally complete, if every its extension is structurally complete. For example, classical logic, as well as the logics LC and Grz.3 mentioned above, are hereditarily structurally complete. A complete description of hereditarily structurally complete superintuitionistic and transitive modal logics was given by Citkin and Rybakov. Namely, a superintuitionistic logic is hereditarily structurally complete if and only if it is not valid in any of the five Kripke frames
Similarly, an extension of K4 is hereditarily structurally complete if and only if it is not valid in any of certain twenty Kripke frames (including the five intuitionistic frames above).
There exist structurally complete logics that are not hereditarily structurally complete: for example, Medvedev's logic
Intermediate logic
In mathematical logic, a superintuitionistic logic is a propositional logic extending intuitionistic logic. Classical logic is the strongest consistent superintuitionistic logic, thus consistent superintuitionistic logics are called intermediate logics .-Definition:A superintuitionistic logic is a...
is structurally complete, but it is included in the structurally incomplete logic KC.
Variants
A rule with parameters is a rule of the form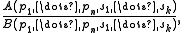
whose variables are divided into the "regular" variables pi, and the parameters si. The rule is L-admissible if every L-unifier σ of A such that σsi = si for each i is also a unifier of B. The basic decidability results for admissible rules also carry to rules with parameters.
A multiple-conclusion rule is a pair (Γ,Δ) of two finite sets of formulas, written as
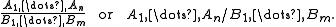
Such a rule is admissible if every unifier of Γ is also a unifier of some formula from Δ. For example, a logic L is consistent iff it admits the rule
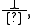
and a superintuitionistic logic has the disjunction property iff it admits the rule
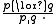
Again, basic results on admissible rules generalize smoothly to multiple-conclusion rules. In logics with a variant of the disjunction property, the multiple-conclusion rules have the same expressive power as single-conclusion rules: for example, in S4 the rule above is equivalent to

Nevertheless, multiple-conclusion rules can often be employed to simplify arguments.
In proof theory
Proof theory
Proof theory is a branch of mathematical logic that represents proofs as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as plain lists, boxed lists, or trees, which are constructed...
, admissibility is often considered in the context of sequent calculi
Sequent calculus
In proof theory and mathematical logic, sequent calculus is a family of formal systems sharing a certain style of inference and certain formal properties. The first sequent calculi, systems LK and LJ, were introduced by Gerhard Gentzen in 1934 as a tool for studying natural deduction in...
, where the basic objects are sequents rather than formulas. For example, one can rephrase the cut-elimination theorem
Cut-elimination theorem
The cut-elimination theorem is the central result establishing the significance of the sequent calculus. It was originally proved by Gerhard Gentzen 1934 in his landmark paper "Investigations in Logical Deduction" for the systems LJ and LK formalising intuitionistic and classical logic respectively...
as saying that the cut-free sequent calculus admits the cut rule
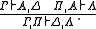
(By abuse of language, it is also sometimes said that the (full) sequent calculus admits cut, meaning its cut-free version does.) However, admissibility in sequent calculi is usually only a notational variant for admissibility in the corresponding logic: any complete calculus for (say) intuitionistic logic admits a sequent rule if and only if IPC admits the formula rule which we obtain by translating each sequent
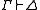 to its characteristic formula
to its characteristic formula 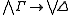 .
.