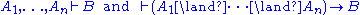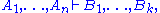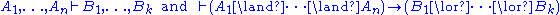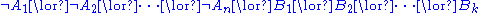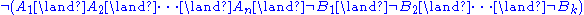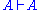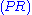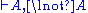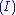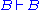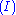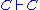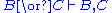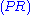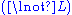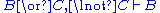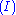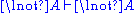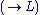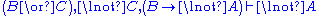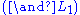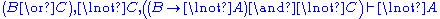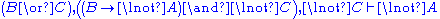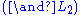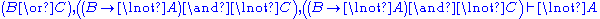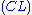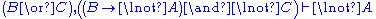Sequent calculus
Encyclopedia
In proof theory
and mathematical logic
, sequent calculus is a family of formal system
s sharing a certain style of inference and certain formal properties. The first sequent calculi, systems LK and LJ, were introduced by Gerhard Gentzen
in 1934 as a tool for studying natural deduction
in first-order logic
(in classical
and intuitionistic
versions, respectively). Gentzen's so-called "Main Theorem" (Hauptsatz) about LK and LJ was the cut-elimination theorem
, a result with far-reaching meta-theoretic
consequences, including consistency
. Gentzen further demonstrated the power and flexibility of this technique a few years later, applying a cut-elimination argument to give a (transfinite) proof of the consistency of Peano arithmetic
, in surprising response to Gödel's incompleteness theorems
. Since this early work, sequent calculi (also called Gentzen systems) and the general concepts relating to them have been widely applied in the fields of proof theory, mathematical logic, and automated deduction.
in the system, i.e., which things may appear as the conclusion of a (sub)proof. The simplest judgment form is used in Hilbert-style deduction system
s, where a judgment has the form
where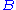
is any formula of first-order-logic (or whatever logic the deduction system applies to, e.g., propositional calculus
or a higher-order logic
or a modal logic
). The theorems are those formulae that appear as the concluding judgment in a valid proof. A Hilbert-style system needs no distinction between formulae and judgments; we make one here solely for comparison with the cases that follow.
The price paid for the simple syntax of a Hilbert-style system is that complete formal proofs tend to get extremely long. Concrete arguments about proofs in such a system almost always appeal to the deduction theorem
. This leads to the idea of including the deduction theorem as a formal rule in the system, which happens in natural deduction
. In natural deduction, judgments have the shape
where the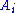
's and 
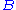are again formulae and 
. In words, a judgment consists of a list (possibly empty) of formulae on the left-hand side of a turnstile
symbol "
", with a single formula on the right-hand side. The theorems are those formulae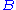 
such that 
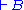(with an empty left-hand side) is the conclusion of a valid proof.
(In some presentations of natural deduction, the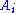
s and the turnstile are not written down explicitly; instead a two-dimensional notation from which they can be inferred is used).
The standard semantics of a judgment in natural deduction is that it asserts that whenever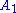
, 
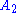, etc., are all true, 
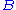will also be true. The judgments
are equivalent in the strong sense that a proof of either one may be extended to a proof of the other.
Finally, sequent calculus generalizes the form of a natural deduction judgment to
a syntactic object called a sequent
. The formulas on left-hand side of the turnstile
are called the antecedent, and the formulas on right-hand side are called the succedent; together they are called cedents. Again,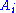
and 
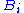are formulae, and 
and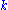 
are nonnegative integers, that is, the left-hand-side or the right-hand-side (or neither or both) may be empty. As in natural deduction, theorems are those 
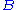where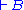 
is the conclusion of a valid proof. The empty sequent, having both cedents empty, is defined to be false.
The standard semantics of a sequent is an assertion that whenever every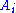
is true, at least one 
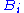will also be true. One way to express this is that a comma to the left of the turnstile should be thought of as an "and", and a comma to the right of the turnstile should be thought of as an (inclusive) "or". The sequents
are equivalent in the strong sense that a proof of either one may be extended to a proof of the other.
At first sight, this extension of the judgment form may appear to be a strange complication — it is not motivated by an obvious shortcoming of natural deduction, and it is initially confusing that the comma seems to mean entirely different things on the two sides of the turnstile. However, in a classical context
the semantics of the sequent can also (by propositional tautology
) be expressed either as
(at least one of the As is false, or one of the Bs is true) or as
(it cannot be the case that all of the As are true and all of the Bs are false). In these formulations, the only difference between formulae on either side of the turnstile is that one side is negated. Thus, swapping left for right in a sequent corresponds to negating all of the constituent formulae. This means that a symmetry such as De Morgan's laws, which manifests itself as logical negation on the semantic level, translates directly into a left-right symmetry of sequents — and indeed, the inference rules in sequent calculus for dealing with conjunction (∧) are mirror images of those dealing with disjunction (∨).
Many logicians feel that this symmetric presentation offers a deeper insight in the structure of the logic than other styles of proof system, where the classical duality of negation is not as apparent in the rules.
A (formal) proof in this calculus is a sequence of sequent
s, where each of the sequents is derivable from sequents appearing earlier in the sequence by using one of the rules
below.
Restrictions: In the rules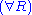
and 
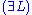, the variable 
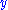must not occur free within 
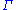and 
. Alternatively, the variable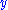 
must not appear anywhere in the respective lower sequents.
. In contrast, the structural rules operate on the structure of the sequents, ignoring the exact shape of the formulae. The two exceptions to this general scheme are the axiom of identity (I) and the rule of (Cut).
Although stated in a formal way, the above rules allow for a very intuitive reading in terms of classical logic. Consider, for example, the rule (∧L1). It says that, whenever one can prove that Δ can be concluded from some sequence of formulae that contain A, then one can also conclude Δ from the (stronger) assumption, that A∧B holds. Likewise, the rule (¬R) states that, if Γ and A suffice to conclude Δ, then from Γ alone one can either still conclude Δ or A must be false, i.e. ¬A holds. All the rules can be interpreted in this way.
For an intuition about the quantifier rules, consider the rule (∀R). Of course concluding that ∀x A holds just from the fact that A[y/x] is true is not in general possible. If, however, the variable y is not mentioned elsewhere (i.e. it can still be chosen freely, without influencing the other formulae), then one may assume, that A[y/x] holds for any value of y. The other rules should then be pretty straightforward.
Instead of viewing the rules as descriptions for legal derivations in predicate logic, one may also consider them as instructions for the construction of a proof for a given statement. In this case the rules can be read bottom-up; for example, (∧R) says that, to prove that A∧B follows from the assumptions Γ and Σ, it suffices to prove that A can be concluded from Γ and B can be concluded from Σ, respectively. Note that, given some antecedent, it is not clear how this is to be split into Γ and Σ. However, there are only finitely many possibilities to be checked since the antecedent by assumption is finite. This also illustrates how proof theory can be viewed as operating on proofs in a combinatorial fashion: given proofs for both A and B, one can construct a proof for A∧B.
When looking for some proof, most of the rules offer more or less direct recipes of how to do this. The rule of cut is different: It states that, when a formula A can be concluded and this formula may also serve as a premise for concluding other statements, then the formula A can be "cut out" and the respective derivations are joined. When constructing a proof bottom-up, this creates the problem of guessing A (since it does not appear at all below). The cut-elimination theorem
is thus crucial to the applications of sequent calculus in automated deduction: it states that all uses of the cut rule can be eliminated from a proof, implying that any provable sequent can be given a cut-free proof.
The second rule that is somewhat special is the axiom of identity (I). The intuitive reading of this is obvious: every formula proves itself. Like the cut rule, the axiom of identity is somewhat redundant: the completeness of atomic initial sequents
states that the rule can be restricted to atomic formula
s without any loss of provability.
Observe that all rules have mirror companions, except the ones for implication. This reflects the fact that the usual language of first-order logic does not include the "is not implied by" connective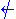
that would be the De Morgan dual of implication. Adding such a connective with its natural rules would make the calculus completely left-right symmetric.
", known as
the Law of excluded middle
(tertium non datur in Latin).
Next is the proof of a simple fact involving quantifiers. Note that the converse is not true, and its falsity can be seen when attempting to derive it bottom-up, because an existing free variable cannot be used in substitution in the rules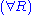
and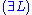 
.
For something more interesting we shall prove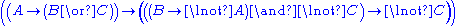
. It is straightforward to find the derivation, which exemplifies the usefulness of LK in automated proving.
These derivations also emphasize the strictly formal structure of the sequent calculus. For example, the logical rules as defined above always act on a formula immediately adjacent to the turnstile, such that the permutation rules are necessary. Note, however, that this is in part an artifact of the presentation, in the original style of Gentzen. A common simplification involves the use of multisets
of formulas in the interpretation of the sequent, rather than sequences, eliminating the need for an explicit permutation rule. This corresponds to shifting commutativity of assumptions and derivations outside the sequent calculus, whereas LK embeds it within the system itself.
Weakening (W) allows the addition of arbitrary elements to a sequence. Intuitively, this is allowed in the antecedent because we can always add assumptions to our proof, and in the succedent because we can always allow for alternative conclusions.
Contraction (C) and Permutation (P) assure that neither the order (P) nor the multiplicity of occurrences (C) of elements of the sequences matters. Thus, one could instead of sequence
s also consider sets.
The extra effort of using sequences, however, is justified since part or all of the structural rules may be omitted. Doing so, one obtains the so-called substructural logic
s.
and complete
with respect to first-order logic, i.e. a statement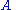
follows semantically
from a set of premises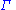
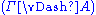iff
the sequent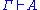
can be derived by the above rules.
In the sequent calculus, the rule of cut is admissible. This result is also referred to as Gentzen's Hauptsatz ("Main Theorem").
First of all, as mentioned above, the sequents can be viewed to consist of sets or multiset
s. In this case, the rules for permuting and (when using sets) contracting formulae are obsolete.
The rule of weakening will become admissible, when the axiom (I) is changed, such that any sequent of the form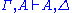
can be concluded. This means that 
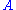proves 
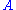in any context. Any weakening that appears in a derivation can then be performed right at the start. This may be a convenient change when constructing proofs bottom-up.
Independent of these one may also change the way in which contexts are split within the rules: In the cases (∧R), (∨L), and (→L) the left context is somehow split into Γ and Σ when going upwards. Since contraction allows for the duplication of these, one may assume that the full context is used in both branches of the derivation. By doing this, one assures that no important premises are lost in the wrong branch. Using weakening, the irrelevant parts of the context can be eliminated later.
systems. They are generally weaker than LK (i.e., they have fewer theorems), and thus not complete with respect to the standard semantics of first-order logic. However, they have other interesting properties that have led to applications in theoretical computer science
and artificial intelligence
.
. To this end, one has to restrict to sequents with exactly one formula on the right-hand side, and modify the rules to maintain this invariant. For example, (∨L) is reformulated as follows (where C is an arbitrary formula):
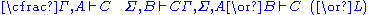
The resulting system is called LJ. It is sound and complete with respect to intuitionistic logic and admits a similar cut-elimination proof.
Proof theory
Proof theory is a branch of mathematical logic that represents proofs as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as plain lists, boxed lists, or trees, which are constructed...
and mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, sequent calculus is a family of formal system
Formal system
In formal logic, a formal system consists of a formal language and a set of inference rules, used to derive an expression from one or more other premises that are antecedently supposed or derived . The axioms and rules may be called a deductive apparatus...
s sharing a certain style of inference and certain formal properties. The first sequent calculi, systems LK and LJ, were introduced by Gerhard Gentzen
Gerhard Gentzen
Gerhard Karl Erich Gentzen was a German mathematician and logician. He had his major contributions in the foundations of mathematics, proof theory, especially on natural deduction and sequent calculus...
in 1934 as a tool for studying natural deduction
Natural deduction
In logic and proof theory, natural deduction is a kind of proof calculus in which logical reasoning is expressed by inference rules closely related to the "natural" way of reasoning...
in first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
(in classical
Classical logic
Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
and intuitionistic
Intuitionistic logic
Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
versions, respectively). Gentzen's so-called "Main Theorem" (Hauptsatz) about LK and LJ was the cut-elimination theorem
Cut-elimination theorem
The cut-elimination theorem is the central result establishing the significance of the sequent calculus. It was originally proved by Gerhard Gentzen 1934 in his landmark paper "Investigations in Logical Deduction" for the systems LJ and LK formalising intuitionistic and classical logic respectively...
, a result with far-reaching meta-theoretic
Metatheory
A metatheory or meta-theory is a theory whose subject matter is some other theory. In other words it is a theory about a theory. Statements made in the metatheory about the theory are called metatheorems....
consequences, including consistency
Consistency
Consistency can refer to:* Consistency , the psychological need to be consistent with prior acts and statements* "Consistency", an 1887 speech by Mark Twain...
. Gentzen further demonstrated the power and flexibility of this technique a few years later, applying a cut-elimination argument to give a (transfinite) proof of the consistency of Peano arithmetic
Gentzen's consistency proof
Gentzen's consistency proof is a result of proof theory in mathematical logic. It "reduces" the consistency of a simplified part of mathematics, not to something that could be proved , but to clarified logical principles.-Gentzen's theorem:In 1936 Gerhard Gentzen proved the consistency of...
, in surprising response to Gödel's incompleteness theorems
Gödel's incompleteness theorems
Gödel's incompleteness theorems are two theorems of mathematical logic that establish inherent limitations of all but the most trivial axiomatic systems capable of doing arithmetic. The theorems, proven by Kurt Gödel in 1931, are important both in mathematical logic and in the philosophy of...
. Since this early work, sequent calculi (also called Gentzen systems) and the general concepts relating to them have been widely applied in the fields of proof theory, mathematical logic, and automated deduction.
Introduction
One way to classify different styles of deduction systems is to look at the form of judgmentsJudgment (mathematical logic)
In mathematical logic, a judgment can be for example an assertion about occurrence of a free variable in an expression of the object language, or about provability of a proposition ; but judgments can be also other inductively definable assertions in the metatheory...
in the system, i.e., which things may appear as the conclusion of a (sub)proof. The simplest judgment form is used in Hilbert-style deduction system
Hilbert-style deduction system
In logic, especially mathematical logic, a Hilbert system, sometimes called Hilbert calculus or Hilbert–Ackermann system, is a type of system of formal deduction attributed to Gottlob Frege and David Hilbert...
s, where a judgment has the form
where
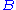is any formula of first-order-logic (or whatever logic the deduction system applies to, e.g., propositional calculusPropositional calculus
In mathematical logic, a propositional calculus or logic is a formal system in which formulas of a formal language may be interpreted as representing propositions. A system of inference rules and axioms allows certain formulas to be derived, called theorems; which may be interpreted as true...
or a higher-order logic
Higher-order logic
In mathematics and logic, a higher-order logic is a form of predicate logic that is distinguished from first-order logic by additional quantifiers and a stronger semantics...
or a modal logic
Modal logic
Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
). The theorems are those formulae that appear as the concluding judgment in a valid proof. A Hilbert-style system needs no distinction between formulae and judgments; we make one here solely for comparison with the cases that follow.
The price paid for the simple syntax of a Hilbert-style system is that complete formal proofs tend to get extremely long. Concrete arguments about proofs in such a system almost always appeal to the deduction theorem
Deduction theorem
In mathematical logic, the deduction theorem is a metatheorem of first-order logic. It is a formalization of the common proof technique in which an implication A → B is proved by assuming A and then proving B from this assumption. The deduction theorem explains why proofs of conditional...
. This leads to the idea of including the deduction theorem as a formal rule in the system, which happens in natural deduction
Natural deduction
In logic and proof theory, natural deduction is a kind of proof calculus in which logical reasoning is expressed by inference rules closely related to the "natural" way of reasoning...
. In natural deduction, judgments have the shape
where the
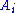's and 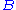are again formulae and . In words, a judgment consists of a list (possibly empty) of formulae on the left-hand side of a turnstileTurnstile (symbol)
In mathematical logic and computer science the symbol \vdash has taken the name turnstile because of its resemblance to a typical turnstile if viewed from above. It is also referred to as tee and is often read as "yields", "proves", "satisfies" or "entails"...
symbol "
", with a single formula on the right-hand side. The theorems are those formulae 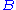such that 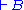(with an empty left-hand side) is the conclusion of a valid proof.(In some presentations of natural deduction, the
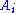s and the turnstile are not written down explicitly; instead a two-dimensional notation from which they can be inferred is used).The standard semantics of a judgment in natural deduction is that it asserts that whenever
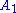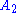, , etc., are all true, 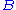will also be true. The judgments
are equivalent in the strong sense that a proof of either one may be extended to a proof of the other.
Finally, sequent calculus generalizes the form of a natural deduction judgment to
a syntactic object called a sequent
Sequent
In proof theory, a sequent is a formalized statement of provability that is frequently used when specifying calculi for deduction. In the sequent calculus, the name sequent is used for the construct which can be regarded as a specific kind of judgment, characteristic to this deduction system.-...
. The formulas on left-hand side of the turnstile
Turnstile
A turnstile, also called a baffle gate, is a form of gate which allows one person to pass at a time. It can also be made so as to enforce one-way traffic of people, and in addition, it can restrict passage only to people who insert a coin, a ticket, a pass, or similar...
are called the antecedent, and the formulas on right-hand side are called the succedent; together they are called cedents. Again,
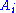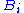and are formulae, and and 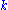are nonnegative integers, that is, the left-hand-side or the right-hand-side (or neither or both) may be empty. As in natural deduction, theorems are thos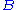e where 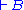is the conclusion of a valid proof. The empty sequent, having both cedents empty, is defined to be false.The standard semantics of a sequent is an assertion that whenever every
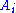is true, at least one 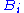will also be true. One way to express this is that a comma to the left of the turnstile should be thought of as an "and", and a comma to the right of the turnstile should be thought of as an (inclusive) "or". The sequents
are equivalent in the strong sense that a proof of either one may be extended to a proof of the other.
At first sight, this extension of the judgment form may appear to be a strange complication — it is not motivated by an obvious shortcoming of natural deduction, and it is initially confusing that the comma seems to mean entirely different things on the two sides of the turnstile. However, in a classical context
Classical logic
Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
the semantics of the sequent can also (by propositional tautology
Tautology (logic)
In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
) be expressed either as
(at least one of the As is false, or one of the Bs is true) or as
(it cannot be the case that all of the As are true and all of the Bs are false). In these formulations, the only difference between formulae on either side of the turnstile is that one side is negated. Thus, swapping left for right in a sequent corresponds to negating all of the constituent formulae. This means that a symmetry such as De Morgan's laws, which manifests itself as logical negation on the semantic level, translates directly into a left-right symmetry of sequents — and indeed, the inference rules in sequent calculus for dealing with conjunction (∧) are mirror images of those dealing with disjunction (∨).
Many logicians feel that this symmetric presentation offers a deeper insight in the structure of the logic than other styles of proof system, where the classical duality of negation is not as apparent in the rules.
The system LK
This section introduces the rules of the sequent calculus LK (which is short for “logistischer klassischer Kalkül”), as introduced by Gentzen in 1934.A (formal) proof in this calculus is a sequence of sequent
Sequent
In proof theory, a sequent is a formalized statement of provability that is frequently used when specifying calculi for deduction. In the sequent calculus, the name sequent is used for the construct which can be regarded as a specific kind of judgment, characteristic to this deduction system.-...
s, where each of the sequents is derivable from sequents appearing earlier in the sequence by using one of the rules
Rule of inference
In logic, a rule of inference, inference rule, or transformation rule is the act of drawing a conclusion based on the form of premises interpreted as a function which takes premises, analyses their syntax, and returns a conclusion...
below.
Inference rules
The following notation will be used:-
known as the turnstileTurnstile (symbol)In mathematical logic and computer science the symbol \vdash has taken the name turnstile because of its resemblance to a typical turnstile if viewed from above. It is also referred to as tee and is often read as "yields", "proves", "satisfies" or "entails"...
, separates the assumptions on the left from the propositions on the right -
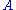and 
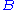denote formulae of first-order predicate logic (one may also restrict this to propositional logic), -
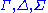, and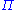 
are finite (possibly empty) sequences of formulae (in fact, the order of formulae do not matter; see subsection Structural Rules), called contexts,
- when on the left of the
, the sequence of formulas is considered conjunctively (all assumed to hold at the same time), - while on the right of the
, the sequence of formulas is considered disjunctively (at least one of the formulas must hold for any assignment of variables),
- when on the left of the
-
denotes an arbitrary term, -
and 
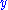denote variables, -
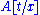denotes the formula that is obtained by substituting the term 
for every free occurrence of the variable 
in formula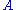 
, - a variable is said to occur freeFree variables and bound variablesIn mathematics, and in other disciplines involving formal languages, including mathematical logic and computer science, a free variable is a notation that specifies places in an expression where substitution may take place...
within a formula if it occurs outside the scope of quantifiers
or 
. -
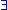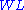and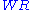 
stand for Weakening Left/Right, 
and 
for Contraction, an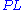d 
and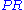 
for Permutation.
| Axiom: | Cut: |
 |  |
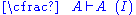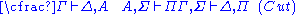| Left logical rules: | Right logical rules: |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
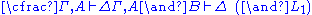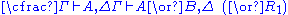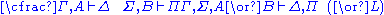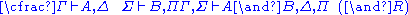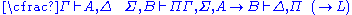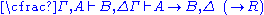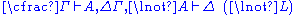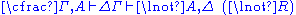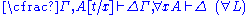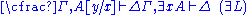| Left structural rules: | Right structural rules: |
 |  |
 |  |
 |  |
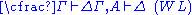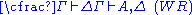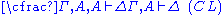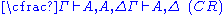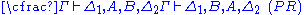Restrictions: In the rules
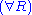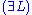and , the variable 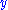must not occur free within 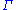and . Alternatively, the variable 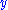must not appear anywhere in the respective lower sequents.An intuitive explanation
The above rules can be divided into two major groups: logical and structural ones. Each of the logical rules introduces a new logical formula either on the left or on the right of the turnstileTurnstile (symbol)
In mathematical logic and computer science the symbol \vdash has taken the name turnstile because of its resemblance to a typical turnstile if viewed from above. It is also referred to as tee and is often read as "yields", "proves", "satisfies" or "entails"...
. In contrast, the structural rules operate on the structure of the sequents, ignoring the exact shape of the formulae. The two exceptions to this general scheme are the axiom of identity (I) and the rule of (Cut).Although stated in a formal way, the above rules allow for a very intuitive reading in terms of classical logic. Consider, for example, the rule (∧L1). It says that, whenever one can prove that Δ can be concluded from some sequence of formulae that contain A, then one can also conclude Δ from the (stronger) assumption, that A∧B holds. Likewise, the rule (¬R) states that, if Γ and A suffice to conclude Δ, then from Γ alone one can either still conclude Δ or A must be false, i.e. ¬A holds. All the rules can be interpreted in this way.
For an intuition about the quantifier rules, consider the rule (∀R). Of course concluding that ∀x A holds just from the fact that A[y/x] is true is not in general possible. If, however, the variable y is not mentioned elsewhere (i.e. it can still be chosen freely, without influencing the other formulae), then one may assume, that A[y/x] holds for any value of y. The other rules should then be pretty straightforward.
Instead of viewing the rules as descriptions for legal derivations in predicate logic, one may also consider them as instructions for the construction of a proof for a given statement. In this case the rules can be read bottom-up; for example, (∧R) says that, to prove that A∧B follows from the assumptions Γ and Σ, it suffices to prove that A can be concluded from Γ and B can be concluded from Σ, respectively. Note that, given some antecedent, it is not clear how this is to be split into Γ and Σ. However, there are only finitely many possibilities to be checked since the antecedent by assumption is finite. This also illustrates how proof theory can be viewed as operating on proofs in a combinatorial fashion: given proofs for both A and B, one can construct a proof for A∧B.
When looking for some proof, most of the rules offer more or less direct recipes of how to do this. The rule of cut is different: It states that, when a formula A can be concluded and this formula may also serve as a premise for concluding other statements, then the formula A can be "cut out" and the respective derivations are joined. When constructing a proof bottom-up, this creates the problem of guessing A (since it does not appear at all below). The cut-elimination theorem
Cut-elimination theorem
The cut-elimination theorem is the central result establishing the significance of the sequent calculus. It was originally proved by Gerhard Gentzen 1934 in his landmark paper "Investigations in Logical Deduction" for the systems LJ and LK formalising intuitionistic and classical logic respectively...
is thus crucial to the applications of sequent calculus in automated deduction: it states that all uses of the cut rule can be eliminated from a proof, implying that any provable sequent can be given a cut-free proof.
The second rule that is somewhat special is the axiom of identity (I). The intuitive reading of this is obvious: every formula proves itself. Like the cut rule, the axiom of identity is somewhat redundant: the completeness of atomic initial sequents
Completeness of atomic initial sequents
In sequent calculus, the completeness of atomic initial sequents states that initial sequents can be derived from only atomic initial sequents . This theorem plays a role analogous to eta expansion in lambda calculus, and dual to cut-elimination and beta reduction...
states that the rule can be restricted to atomic formula
Atomic formula
In mathematical logic, an atomic formula is a formula with no deeper propositional structure, that is, a formula that contains no logical connectives or equivalently a formula that has no strict subformulas. Atoms are thus the simplest well-formed formulas of the logic...
s without any loss of provability.
Observe that all rules have mirror companions, except the ones for implication. This reflects the fact that the usual language of first-order logic does not include the "is not implied by" connective
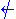that would be the De Morgan dual of implication. Adding such a connective with its natural rules would make the calculus completely left-right symmetric.Example derivations
Here is the derivation of "", known asthe Law of excluded middle
Law of excluded middle
In logic, the law of excluded middle is the third of the so-called three classic laws of thought. It states that for any proposition, either that proposition is true, or its negation is....
(tertium non datur in Latin).
 | ||
 | ||
 | ||
 | ||
 | ||
 | ||
 | ||
 | ||
 | ||
 | ||
 | ||
 | ||
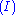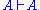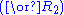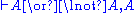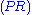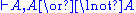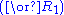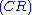Next is the proof of a simple fact involving quantifiers. Note that the converse is not true, and its falsity can be seen when attempting to derive it bottom-up, because an existing free variable cannot be used in substitution in the rules
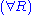and . | ||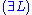
 | ||
 | ||
 | ||
 | ||
 | ||
 | ||
 | ||
 | ||
 | ||
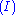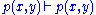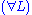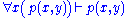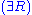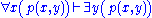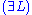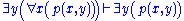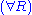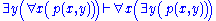For something more interesting we shall prove
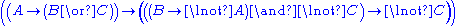. It is straightforward to find the derivation, which exemplifies the usefulness of LK in automated proving.
|  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
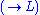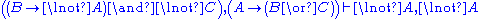These derivations also emphasize the strictly formal structure of the sequent calculus. For example, the logical rules as defined above always act on a formula immediately adjacent to the turnstile, such that the permutation rules are necessary. Note, however, that this is in part an artifact of the presentation, in the original style of Gentzen. A common simplification involves the use of multisets
Multiset
In mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
of formulas in the interpretation of the sequent, rather than sequences, eliminating the need for an explicit permutation rule. This corresponds to shifting commutativity of assumptions and derivations outside the sequent calculus, whereas LK embeds it within the system itself.
Structural rules
The structural rules deserve some additional discussion.Weakening (W) allows the addition of arbitrary elements to a sequence. Intuitively, this is allowed in the antecedent because we can always add assumptions to our proof, and in the succedent because we can always allow for alternative conclusions.
Contraction (C) and Permutation (P) assure that neither the order (P) nor the multiplicity of occurrences (C) of elements of the sequences matters. Thus, one could instead of sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s also consider sets.
The extra effort of using sequences, however, is justified since part or all of the structural rules may be omitted. Doing so, one obtains the so-called substructural logic
Substructural logic
In logic, a substructural logic is a logic lacking one of the usual structural rules , such as weakening, contraction or associativity...
s.
Properties of the system LK
This system of rules can be shown to be both soundSoundness
In mathematical logic, a logical system has the soundness property if and only if its inference rules prove only formulas that are valid with respect to its semantics. In most cases, this comes down to its rules having the property of preserving truth, but this is not the case in general. The word...
and complete
Completeness
In general, an object is complete if nothing needs to be added to it. This notion is made more specific in various fields.-Logical completeness:In logic, semantic completeness is the converse of soundness for formal systems...
with respect to first-order logic, i.e. a statement
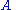follows semanticallySemantics
Semantics is the study of meaning. It focuses on the relation between signifiers, such as words, phrases, signs and symbols, and what they stand for, their denotata....
from a set of premises
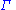
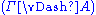iffIFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
the sequent
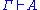can be derived by the above rules.In the sequent calculus, the rule of cut is admissible. This result is also referred to as Gentzen's Hauptsatz ("Main Theorem").
Minor structural alternatives
There is some freedom of choice regarding the technical details of how sequents and structural rules are formalized. As long as every derivation in LK can be effectively transformed to a derivation using the new rules and vice versa, the modified rules may still be called LK.First of all, as mentioned above, the sequents can be viewed to consist of sets or multiset
Multiset
In mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
s. In this case, the rules for permuting and (when using sets) contracting formulae are obsolete.
The rule of weakening will become admissible, when the axiom (I) is changed, such that any sequent of the form
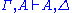can be concluded. This means that 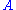proves 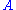in any context. Any weakening that appears in a derivation can then be performed right at the start. This may be a convenient change when constructing proofs bottom-up.Independent of these one may also change the way in which contexts are split within the rules: In the cases (∧R), (∨L), and (→L) the left context is somehow split into Γ and Σ when going upwards. Since contraction allows for the duplication of these, one may assume that the full context is used in both branches of the derivation. By doing this, one assures that no important premises are lost in the wrong branch. Using weakening, the irrelevant parts of the context can be eliminated later.
Substructural logics
Alternatively, one may restrict or forbid the use of some of the structural rules. This yields a variety of substructural logicSubstructural logic
In logic, a substructural logic is a logic lacking one of the usual structural rules , such as weakening, contraction or associativity...
systems. They are generally weaker than LK (i.e., they have fewer theorems), and thus not complete with respect to the standard semantics of first-order logic. However, they have other interesting properties that have led to applications in theoretical computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
and artificial intelligence
Artificial intelligence
Artificial intelligence is the intelligence of machines and the branch of computer science that aims to create it. AI textbooks define the field as "the study and design of intelligent agents" where an intelligent agent is a system that perceives its environment and takes actions that maximize its...
.
Intuitionistic sequent calculus: System LJ
Surprisingly, some small changes in the rules of LK suffice to turn it into a proof system for intuitionistic logicIntuitionistic logic
Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
. To this end, one has to restrict to sequents with exactly one formula on the right-hand side, and modify the rules to maintain this invariant. For example, (∨L) is reformulated as follows (where C is an arbitrary formula):
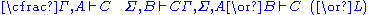
The resulting system is called LJ. It is sound and complete with respect to intuitionistic logic and admits a similar cut-elimination proof.