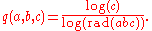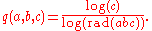Abc conjecture
Encyclopedia
The abc conjecture is a conjecture
in number theory
, first proposed by Joseph Oesterlé
and David Masser
in 1985. The conjecture is stated in terms of three positive integers, a, b and c (whence comes the name), which have no common factor and satisfy a + b = c. If d denotes the product of the distinct prime factor
s of abc, the conjecture essentially states that d is rarely much smaller than c.
Although there is no obvious strategy for resolving the problem, it has already become well known for the number of interesting consequences it entails. Dorian M. Goldfeld
described the abc conjecture as "the most important unsolved problem in Diophantine analysis".
s of n. For example
If a, b, and c are coprime
positive integers such that a + b = c, it turns out that
"usually" c < rad(abc). The abc conjecture deals with the exceptions. Specifically, it states that for every ε>0 there exist only finitely many triples (a,b,c) of positive coprime integers with a + b = c such that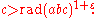
An equivalent formulation states that for any ε > 0, there exists a constant K such that, for all triples of coprime positive integers (a, b, c) satisfying a + b = c, the inequality
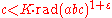
holds.
A third formulation of the conjecture involves the quality
q(a, b, c) of the
triple (a, b, c), defined by:
For example
A typical triple (a, b, c) of coprime positive integers with a + b = c will have c < rad(abc), i.e. q(a, b, c) < 1. Triples with q > 1 such as in the second example are rather special, they consist of numbers divisible by high powers of small prime numbers.
The abc conjecture states that, for any ε > 0, there exist only finitely many triples (a, b, c) of coprime positive integers with a + b = c such that q(a, b, c) > 1 + ε.
Whereas it is known that there are infinitely many triples (a, b, c) of coprime positive integers with a + b = c such that q(a, b, c) > 1, the conjecture predicts that only finitely many of those have q > 1.01 or q > 1.001 or even q > 1.0001, etc.
As a and c together contribute only a factor of two to the radical, while b is divisible by 9, rad(abc) < 2c/3 for these examples. By replacing the exponent 6n by other exponents forcing b to have larger square factors, the ratio between the radical and c may be made arbitrarily large. Another triple with a particularly small radical was found by Eric Reyssat:
.
While the first group of these have now been proven, the abc conjecture itself remains of interest, because of its numerous links with deep questions in number theory.
ed by a near-linear function of the radical of abc, as the abc conjecture states, or even whether it can be bounded by a polynomial
of rad(abc). However, exponential
bounds are known. Specifically, the following bounds have been proven:
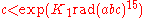(C. L. Stewart
& R. Tijdeman
1986),
(C. L. Stewart & Kunrui Yu 1991), and
(C. L. Stewart & Kunrui Yu 2001).
In these bounds, K1 is a constant
that does not depend on a, b, or c, and K2 and K3 are constants that depend on ε (in an effectively computable way) but not on a, b, or c. The bounds apply to any triple for which c > 2.
in the Netherlands, together with the Dutch Kennislink science institute, launched the ABC@Home
project, a grid computing
system which aims to discover additional triples a, b, c with rad(abc) < c. Although no finite set of examples or counterexamples can resolve the abc conjecture, it is hoped that patterns in the triples discovered by this project will lead to insights about the conjecture and about number theory more generally.
, ABC@Home has found 20.9 million triples, and its present goal is to obtain a complete list of all ABC triples (a,b,c) with c no more than 1020.
where the quality q(a, b, c) of the triple (a, b, c), defined by:
where ω is the total number of distinct primes dividing a, b and c. A related conjecture of Andrew Granville
states that on the RHS we could also put
where Θ(n) is the number of integers up to n divisible only by primes dividing n.
In 1994, Jerzy Browkin and Juliusz Brzeziński formulated the n-conjecture—a version of the abc conjecture involving
integers.
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, first proposed by Joseph Oesterlé
Joseph Oesterlé
Joseph Oesterlé is a French mathematician who, along with David Masser, formulated the abc conjecture in 1985. It is perhaps the most important unsolved problem in diophantine analysis.-External links:*...
and David Masser
David Masser
David William Masser is Professor of Mathematics at the University of Basel, in Basel, Switzerland. He obtained his Ph.D. from University of Cambridge in 1974 on the topic of Elliptic Functions and Transcendence....
in 1985. The conjecture is stated in terms of three positive integers, a, b and c (whence comes the name), which have no common factor and satisfy a + b = c. If d denotes the product of the distinct prime factor
Prime factor
In number theory, the prime factors of a positive integer are the prime numbers that divide that integer exactly, without leaving a remainder. The process of finding these numbers is called integer factorization, or prime factorization. A prime factor can be visualized by understanding Euclid's...
s of abc, the conjecture essentially states that d is rarely much smaller than c.
Although there is no obvious strategy for resolving the problem, it has already become well known for the number of interesting consequences it entails. Dorian M. Goldfeld
Dorian M. Goldfeld
Dorian Morris Goldfeld is an American mathematician.He received his B.S. degree in 1967 from Columbia University. His doctoral dissertation entitled "Some Methods of Averaging in the Analytical Theory of Numbers" was completed under the supervision of Patrick X. Gallagher in 1969, also at Columbia...
described the abc conjecture as "the most important unsolved problem in Diophantine analysis".
Formulations
For a positive integer n, the radical of n, denoted rad(n), is the product of the distinct prime factorPrime factor
In number theory, the prime factors of a positive integer are the prime numbers that divide that integer exactly, without leaving a remainder. The process of finding these numbers is called integer factorization, or prime factorization. A prime factor can be visualized by understanding Euclid's...
s of n. For example
- rad(16) = rad(24) = 2,
- rad(17) = 17,
- rad(18) = rad(2·32) = 2·3 = 6.
If a, b, and c are coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
positive integers such that a + b = c, it turns out that
"usually" c < rad(abc). The abc conjecture deals with the exceptions. Specifically, it states that for every ε>0 there exist only finitely many triples (a,b,c) of positive coprime integers with a + b = c such that
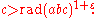
An equivalent formulation states that for any ε > 0, there exists a constant K such that, for all triples of coprime positive integers (a, b, c) satisfying a + b = c, the inequality
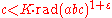
holds.
A third formulation of the conjecture involves the quality
q(a, b, c) of the
triple (a, b, c), defined by:
For example
- q(4, 127, 131) = log(131) / log(rad(4·127·131)) = log(131) / log(2·127·131) = 0.46820...
- q(3, 125, 128) = log(128) / log(rad(3·125·128)) = log(128) / log(30) = 1.426565...
A typical triple (a, b, c) of coprime positive integers with a + b = c will have c < rad(abc), i.e. q(a, b, c) < 1. Triples with q > 1 such as in the second example are rather special, they consist of numbers divisible by high powers of small prime numbers.
The abc conjecture states that, for any ε > 0, there exist only finitely many triples (a, b, c) of coprime positive integers with a + b = c such that q(a, b, c) > 1 + ε.
Whereas it is known that there are infinitely many triples (a, b, c) of coprime positive integers with a + b = c such that q(a, b, c) > 1, the conjecture predicts that only finitely many of those have q > 1.01 or q > 1.001 or even q > 1.0001, etc.
Examples of triples with small radical
The condition that ε > 0 is necessary for the truth of the conjecture, as there exist infinitely many triples a, b, c with rad(abc) < c. For instance, such a triple may be taken as- a = 1
- b = 26n − 1
- c = 26n.
As a and c together contribute only a factor of two to the radical, while b is divisible by 9, rad(abc) < 2c/3 for these examples. By replacing the exponent 6n by other exponents forcing b to have larger square factors, the ratio between the radical and c may be made arbitrarily large. Another triple with a particularly small radical was found by Eric Reyssat:
- a = 2:
- b = 310 109 = 6436341
- c = 235 = 6436343
- rad(abc) = 15042.
Some consequences
The conjecture has not been proven, but it has a large number of interesting consequences. These include both known results, and conjectures for which it gives a conditional proofConditional proof
A conditional proof is a proof that takes the form of asserting a conditional, and proving that the antecedent of the conditional necessarily leads to the consequent....
.
- Thue–Siegel–Roth theoremThue–Siegel–Roth theoremIn mathematics, the Thue–Siegel–Roth theorem, also known simply as Roth's theorem, is a foundational result in diophantine approximation to algebraic numbers. It is of a qualitative type, stating that a given algebraic number α may not have too many rational number approximations, that are 'very...
on diophantine approximation of algebraic numbers - Fermat's Last TheoremFermat's Last TheoremIn number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
for all sufficiently large exponents (proven in general by Andrew WilesAndrew WilesSir Andrew John Wiles KBE FRS is a British mathematician and a Royal Society Research Professor at Oxford University, specializing in number theory...
) - The Mordell conjecture (proven by Gerd FaltingsGerd FaltingsGerd Faltings is a German mathematician known for his work in arithmetic algebraic geometry.From 1972 to 1978, he studied mathematics and physics at the University of Münster. In 1978 he received his PhD in mathematics and in 1981 he got the venia legendi in mathematics, both from the University...
) - The Erdős–Woods conjectureErdos–Woods numberIn number theory, an Erdős–Woods number is a positive integer that has the following property:Consider a sequence of consecutive positive integers [a, a+1, \dots, a+k]. The number k is an Erdős–Woods number if there exists such a sequence, beginning with some number a, in which each of the elements...
except for a finite number of counterexamples - The existence of infinitely many non-Wieferich primesWieferich primeIn number theory, a Wieferich prime is a prime number p such that p2 divides 2p − 1 − 1, therefore connecting these primes with Fermat's little theorem, which states that every odd prime p divides 2p − 1 − 1...
- The weak form of Marshall Hall's conjectureMarshall Hall's conjectureIn mathematics, Marshall Hall's conjecture is an open question, , on the differences between perfect squares and perfect cubes. Aside from the case of a perfect sixth power, it asserts that a perfect square m2 and a perfect cube n3 must lie a substantial distance apart...
on the separation between squares and cubes of integers - The Fermat–Catalan conjectureFermat–Catalan conjectureIn number theory, the Fermat–Catalan conjecture combines ideas of Fermat's last theorem and the Catalan conjecture, hence the name. The conjecture states that the equation...
, a generalization of Fermat's last theorem concerning powers that are sums of powers - The L function L(s,(−d/.)) formed with the Legendre symbolLegendre symbolIn number theory, the Legendre symbol is a multiplicative function with values 1, −1, 0 that is a quadratic character modulo a prime number p: its value on a quadratic residue mod p is 1 and on a quadratic non-residue is −1....
, has no Siegel zeroSiegel zeroIn mathematics, more specifically in the field of analytic number theory, a Siegel zero, named after Carl Ludwig Siegel, is a type of potential counterexample to the generalized Riemann hypothesis, on the zeroes of Dirichlet L-function....
(this consequence actually requires a uniform version of the abc conjecture in number fields, not only the abc conjecture as formulated above for rational integers) - P(x) has only finitely many perfect powers for integralIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
x for P a polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
with at least three simple zeros. - A generalization of Tijdeman's theoremTijdeman's theoremIn number theory, Tijdeman's theorem states that there are at most a finite number of consecutive powers. Stated another way, the set of solutions in integers x, y, n, m of the exponential diophantine equationy^m = x^n + 1,\...
- It is equivalent to the Granville–Langevin conjecture
- It is equivalent to the modified Szpiro conjecture.
- Dąbrowski (1996) has shown that the abc conjecture implies that n! + A= k2 has only finitely many solutions for any given integer A.
While the first group of these have now been proven, the abc conjecture itself remains of interest, because of its numerous links with deep questions in number theory.
Theoretical results
It remains unknown whether c can be upper boundUpper bound
In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
ed by a near-linear function of the radical of abc, as the abc conjecture states, or even whether it can be bounded by a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
of rad(abc). However, exponential
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
bounds are known. Specifically, the following bounds have been proven:
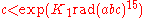(C. L. StewartCameron Leigh Stewart
Cameron Leigh Stewart is a Canadian mathematician. He is currently a professor of mathematics at the University of Waterloo. He was elected Fellow of the Royal Society of Canada in 1989. He was appointed Fellow of the Fields Institute in 2008. Since 2003 he has held a Canada Research Chair . Since...
& R. Tijdeman
Robert Tijdeman
Robert Tijdeman is a Dutch mathematician. Specializing in number theory, he is best known for his Tijdeman's theorem. He is a professor of mathematics at the Leiden University since 1975, and was chairman of the department of mathematics and computer science at Leiden from 1991 to 1993...
1986),
(C. L. Stewart & Kunrui Yu 1991), and (C. L. Stewart & Kunrui Yu 2001).In these bounds, K1 is a constant
Constant (mathematics)
In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition to variable In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition...
that does not depend on a, b, or c, and K2 and K3 are constants that depend on ε (in an effectively computable way) but not on a, b, or c. The bounds apply to any triple for which c > 2.
Computational results
In 2006, the Mathematics Department of Leiden UniversityLeiden University
Leiden University , located in the city of Leiden, is the oldest university in the Netherlands. The university was founded in 1575 by William, Prince of Orange, leader of the Dutch Revolt in the Eighty Years' War. The royal Dutch House of Orange-Nassau and Leiden University still have a close...
in the Netherlands, together with the Dutch Kennislink science institute, launched the ABC@Home
ABC@Home
ABC@Home is an educational and non-profit network computing project finding abc-triples related to the abc conjecture in number theory.Using the Berkeley Open Infrastructure for Network Computing distributed computing platform...
project, a grid computing
Grid computing
Grid computing is a term referring to the combination of computer resources from multiple administrative domains to reach a common goal. The grid can be thought of as a distributed system with non-interactive workloads that involve a large number of files...
system which aims to discover additional triples a, b, c with rad(abc) < c. Although no finite set of examples or counterexamples can resolve the abc conjecture, it is hoped that patterns in the triples discovered by this project will lead to insights about the conjecture and about number theory more generally.
| q > 1 | q > 1.05 | q > 1.1 | q > 1.2 | q > 1.3 | q > 1.4 | |
|---|---|---|---|---|---|---|
| c < 102 | 6 | 4 | 4 | 2 | 0 | 0 |
| c < 103 | 31 | 17 | 14 | 8 | 3 | 1 |
| c < 104 | 120 | 74 | 50 | 22 | 8 | 3 |
| c < 105 | 418 | 240 | 152 | 51 | 13 | 6 |
| c < 106 | 1.268 | 667 | 379 | 102 | 29 | 11 |
| c < 107 | 3.499 | 1.669 | 856 | 210 | 60 | 17 |
| c < 108 | 8.987 | 3.869 | 1.801 | 384 | 98 | 25 |
| c < 109 | 22.316 | 8.742 | 3.693 | 706 | 144 | 34 |
| c < 1010 | 51.677 | 18.233 | 7.035 | 1.159 | 218 | 51 |
| c < 1011 | 116.978 | 37.612 | 13.266 | 1.947 | 327 | 64 |
| c < 1012 | 252.856 | 73.714 | 23.773 | 3.028 | 455 | 74 |
| c < 1013 | 528.275 | 139.762 | 41.438 | 4.519 | 599 | 84 |
| c < 1014 | 1.075.319 | 258.168 | 70.047 | 6.665 | 769 | 98 |
| c < 1015 | 2.131.671 | 463.446 | 115.041 | 9.497 | 998 | 112 |
| c < 1016 | 4.119.410 | 812.499 | 184.727 | 13.118 | 1.232 | 126 |
| c < 1017 | 7.801.334 | 1.396.909 | 290.965 | 17.890 | 1.530 | 143 |
| c < 1018 | 14.482.059 | 2.352.105 | 449.194 | 24.013 | 1.843 | 160 |
, ABC@Home has found 20.9 million triples, and its present goal is to obtain a complete list of all ABC triples (a,b,c) with c no more than 1020.
| q | a | b | c | Discovered by | |
|---|---|---|---|---|---|
| 1 | 1.6299 | 2 | 310109 | 235 | Eric Reyssat |
| 2 | 1.6260 | 112 | 325673 | 22123 | Benne de Weger |
| 3 | 1.6235 | 19·1307 | 7·292318 | 2832254 | Jerzy Browkin, Juliusz Brzezinski |
| 4 | 1.5444 | 724123113 | 111613279 | 2·33523953 | Abderrahmane Nitaj |
| 5 | 1.4805 | 52279·45949 | 321318613 | 223174251217333 | Frank Rubin |
where the quality q(a, b, c) of the triple (a, b, c), defined by:
Refined forms and generalizations
A stronger inequality proposed in 1996 by Alan Baker states that in the inequality, one can replace rad(abc) by- ε−ωrad(abc),
where ω is the total number of distinct primes dividing a, b and c. A related conjecture of Andrew Granville
Andrew Granville
Andrew James Granville is a British mathematician, working in the field of number theory.He has been a faculty member at the Université de Montréal since 2002. Before moving to Montreal he was a mathematics professor at University of Georgia from 1991 until 2002...
states that on the RHS we could also put
- O(rad(abc) Θ(rad(abc)))
where Θ(n) is the number of integers up to n divisible only by primes dividing n.
In 1994, Jerzy Browkin and Juliusz Brzeziński formulated the n-conjecture—a version of the abc conjecture involving
integers.External links
- ABC@home Distributed ComputingDistributed computingDistributed computing is a field of computer science that studies distributed systems. A distributed system consists of multiple autonomous computers that communicate through a computer network. The computers interact with each other in order to achieve a common goal...
project called ABC@HomeABC@HomeABC@Home is an educational and non-profit network computing project finding abc-triples related to the abc conjecture in number theory.Using the Berkeley Open Infrastructure for Network Computing distributed computing platform...
. - Easy as ABC: Easy to follow, detailed explanation by Brian Hayes.
- Abderrahmane Nitaj's ABC conjecture home page
- Bart de Smit's ABC Triples webpage
- http://www.math.columbia.edu/~goldfeld/ABC-Conjecture.pdf
- The amazing ABC conjecture
- The ABC's of Number Theory by Noam D. Elkies