Upper bound
Encyclopedia
In mathematics
, especially in order theory
, an upper bound of a subset
S of some partially ordered set
(P, ≤) is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually
as an element of P which is lesser than or equal to every element of S. A set with an upper bound is said to be bounded from above by that bound, a set with a lower bound is said to be bounded from below by that bound. The terms bounded above (bounded below) are also used in the mathematical literature for sets that have upper (respectively lower) bounds.
, any element greater than or equal to an upper bound of S is again an upper bound of S, and any element lesser than or equal to any lower bound of S is again a lower bound of S. This leads to the consideration of least upper bounds (or suprema) and greatest lower bounds (or infima).
The bounds of a subset S of a partially ordered set P may or may not be elements of S itself. If S contains an upper bound then that upper bound is unique and is called the greatest element
of S. The greatest element of S (if it exists) is also the least upper bound of S. A special situation does occur when a subset is equal to the set of lower bounds of its own set of upper bounds. This observation leads to the definition of Dedekind cut
s.
The empty subset Φ of a partially ordered set P is conventionally considered to be both bounded from above and bounded from below with every element of P being both an upper and lower bound of Φ.
Every subset of the natural numbers has a lower bound, since the natural numbers have a least element (0, or 1 depending on the exact definition of natural numbers). An infinite subset of the natural numbers cannot be bounded from above. An infinite subset of the integers may be bounded from below or bounded from above, but not both. An infinite subset of the rational numbers may or may not be bounded from below and may or may not be bounded from above.
Every finite subset of a totally ordered set has both upper and lower bounds.
.
Given a set S of functions with domain
F and a partially ordered set as codomain
, a function g with domain
is an upper bound of S if 
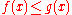for each function f in S and for each x in F. In particular, g is said to be an upper bound of f when S consists of only one function f (i.e. S is a singleton). This does not imply that f is a lower bound of g.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in order theory
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
, an upper bound of a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
S of some partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
(P, ≤) is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually
Duality (order theory)
In the mathematical area of order theory, every partially ordered set P gives rise to a dual partially ordered set which is often denoted by Pop or Pd. This dual order Pop is defined to be the set with the inverse order, i.e. x ≤ y holds in Pop if and only if y ≤ x holds in P...
as an element of P which is lesser than or equal to every element of S. A set with an upper bound is said to be bounded from above by that bound, a set with a lower bound is said to be bounded from below by that bound. The terms bounded above (bounded below) are also used in the mathematical literature for sets that have upper (respectively lower) bounds.
Properties
A subset S of a partially ordered set P may fail to have any bounds or may have many different upper and lower bounds. By transitivityTransitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
, any element greater than or equal to an upper bound of S is again an upper bound of S, and any element lesser than or equal to any lower bound of S is again a lower bound of S. This leads to the consideration of least upper bounds (or suprema) and greatest lower bounds (or infima).
The bounds of a subset S of a partially ordered set P may or may not be elements of S itself. If S contains an upper bound then that upper bound is unique and is called the greatest element
Greatest element
In mathematics, especially in order theory, the greatest element of a subset S of a partially ordered set is an element of S which is greater than or equal to any other element of S. The term least element is defined dually...
of S. The greatest element of S (if it exists) is also the least upper bound of S. A special situation does occur when a subset is equal to the set of lower bounds of its own set of upper bounds. This observation leads to the definition of Dedekind cut
Dedekind cut
In mathematics, a Dedekind cut, named after Richard Dedekind, is a partition of the rationals into two non-empty parts A and B, such that all elements of A are less than all elements of B, and A contains no greatest element....
s.
The empty subset Φ of a partially ordered set P is conventionally considered to be both bounded from above and bounded from below with every element of P being both an upper and lower bound of Φ.
Examples
2 and 5 are both lower bounds for the set { 5, 10, 34, 13934 }, but 8 is not. 42 is both an upper and a lower bound for the set { 42 }; all other numbers are either an upper bound or a lower bound for that set.Every subset of the natural numbers has a lower bound, since the natural numbers have a least element (0, or 1 depending on the exact definition of natural numbers). An infinite subset of the natural numbers cannot be bounded from above. An infinite subset of the integers may be bounded from below or bounded from above, but not both. An infinite subset of the rational numbers may or may not be bounded from below and may or may not be bounded from above.
Every finite subset of a totally ordered set has both upper and lower bounds.
Bounds of functions
The definitions can be generalised to sets of functionsFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
.
Given a set S of functions with domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
F and a partially ordered set as codomain
Codomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
, a function g with domain
is an upper bound of S if 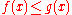for each function f in S and for each x in F. In particular, g is said to be an upper bound of f when S consists of only one function f (i.e. S is a singleton). This does not imply that f is a lower bound of g.