Vandermonde matrix
Encyclopedia
In linear algebra
, a Vandermonde matrix, named after Alexandre-Théophile Vandermonde
, is a matrix with the terms of a geometric progression
in each row, i.e., an m × n matrix
or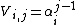
for all indices i and j. (Some authors use the transpose
of the above matrix.)
The determinant
of a square Vandermonde matrix (where m = n) can be expressed as:
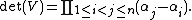
This is called the Vandermonde determinant or Vandermonde polynomial. If all the numbers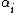
are distinct, then it is non-zero.
The Vandermonde determinant is sometimes called the discriminant
, although many sources, including this article, refer to the discriminant as the square of this determinant. Note that the Vandermonde determinant is alternating in the entries, meaning that permuting the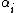
by an odd permutation changes the sign, while permuting them by an even permutation does not change the value of the determinant. It thus depends on the order, while its square (the discriminant) does not depend on the order.
When two or more αi are equal, the corresponding polynomial interpolation
problem (see below) is underdetermined
. In that case one may use a generalization called confluent Vandermonde matrices, which makes the matrix non-singular while retaining most properties. If αi = αi + 1 = ... = αi+k and αi ≠ αi − 1, then the (i + k)th row is given by
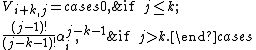
The above formula for confluent Vandermonde matrices can be readily derived by letting two parameters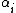
and 
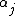go arbitrarily close to each other. The difference vector between the rows corresponding to 
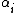and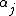 
scaled to a constant yields the above equation (for k = 1). Similarly, the cases k > 1 are obtained by higher order differences. Consequently, the confluent rows are derivatives of the original Vandermonde row.
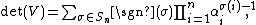
where Sn denotes the set of permutation
s of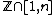
, and sgn(σ) denotes the signature
of the permutation σ, we can rewrite the Vandermonde determinant as
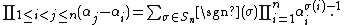
The Vandermonde polynomial (multiplied with the symmetric polynomial
s) generates all the alternating polynomial
s.
If m ≤ n, then the matrix V has maximum rank (m) if and only if
all αi are distinct. A square Vandermonde matrix is thus invertible if and only if the αi are distinct; an explicit formula for the inverse is known.
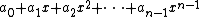to the values the polynomial takes at the points 
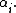The non-vanishing of the Vandermonde determinant for distinct points 
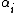shows that, for distinct points, the map from coefficients to values at those points is a one-to-one correspondence, and thus that the polynomial interpolation problem is solvable with unique solution; this result is called the unisolvence theorem.
They are thus useful in polynomial interpolation
, since solving the system of linear equations Vu = y for u with V an m × n Vandermonde matrix is equivalent to finding the coefficient
s uj of the polynomial(s)
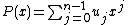
of degree ≤ n − 1 which has (have) the property
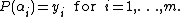
The Vandermonde matrix can easily be inverted in terms of Lagrange basis polynomials: each column is the coefficients of the Lagrange basis polynomial, with terms in increasing order going down. The resulting solution to the interpolation problem is called the Lagrange polynomial
.
The Vandermonde determinant plays a central role in the Frobenius formula, which gives the character
of conjugacy class
es of representation
s of the symmetric group
.
When the values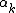
range over powers of a finite field
, then the determinant
has a number of interesting properties: for example, in proving the properties of a BCH code
.
Confluent Vandermonde matrices are used in Hermite interpolation
.
A commonly known special Vandermonde matrix is the discrete Fourier transform
matrix (DFT matrix
), where the numbers αi are chosen equal to the m different mth roots of unity
.
The Vandermonde matrix diagonalizes a companion matrix.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a Vandermonde matrix, named after Alexandre-Théophile Vandermonde
Alexandre-Théophile Vandermonde
Alexandre-Théophile Vandermonde was a French musician, mathematician and chemist who worked with Bézout and Lavoisier; his name is now principally associated with determinant theory in mathematics. He was born in Paris, and died there.Vandermonde was a violinist, and became engaged with...
, is a matrix with the terms of a geometric progression
Geometric progression
In mathematics, a geometric progression, also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed non-zero number called the common ratio. For example, the sequence 2, 6, 18, 54, ... is a geometric progression...
in each row, i.e., an m × n matrix
or
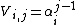
for all indices i and j. (Some authors use the transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
of the above matrix.)
The determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of a square Vandermonde matrix (where m = n) can be expressed as:
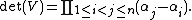
This is called the Vandermonde determinant or Vandermonde polynomial. If all the numbers
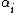are distinct, then it is non-zero.The Vandermonde determinant is sometimes called the discriminant
Discriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
, although many sources, including this article, refer to the discriminant as the square of this determinant. Note that the Vandermonde determinant is alternating in the entries, meaning that permuting the
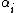by an odd permutation changes the sign, while permuting them by an even permutation does not change the value of the determinant. It thus depends on the order, while its square (the discriminant) does not depend on the order.When two or more αi are equal, the corresponding polynomial interpolation
Polynomial interpolation
In numerical analysis, polynomial interpolation is the interpolation of a given data set by a polynomial: given some points, find a polynomial which goes exactly through these points.- Applications :...
problem (see below) is underdetermined
Underdetermined system
In mathematics, a system of linear equations is considered underdetermined if there are fewer equations than unknowns. The terminology can be described in terms of the concept of counting constraints. Each unknown can be seen as an available degree of freedom...
. In that case one may use a generalization called confluent Vandermonde matrices, which makes the matrix non-singular while retaining most properties. If αi = αi + 1 = ... = αi+k and αi ≠ αi − 1, then the (i + k)th row is given by
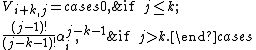
The above formula for confluent Vandermonde matrices can be readily derived by letting two parameters
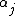and go arbitrarily close to each other. The difference vector between the rows corresponding to 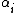and 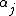scaled to a constant yields the above equation (for k = 1). Similarly, the cases k > 1 are obtained by higher order differences. Consequently, the confluent rows are derivatives of the original Vandermonde row.Properties
Using the Leibniz formula for the determinant,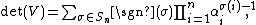where Sn denotes the set of permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s of
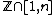, and sgn(σ) denotes the signatureEven and odd permutations
In mathematics, when X is a finite set of at least two elements, the permutations of X fall into two classes of equal size: the even permutations and the odd permutations...
of the permutation σ, we can rewrite the Vandermonde determinant as
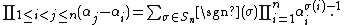
The Vandermonde polynomial (multiplied with the symmetric polynomial
Symmetric polynomial
In mathematics, a symmetric polynomial is a polynomial P in n variables, such that if any of the variables are interchanged, one obtains the same polynomial...
s) generates all the alternating polynomial
Alternating polynomial
In algebra, an alternating polynomial is a polynomial f such that if one switches any two of the variables, the polynomial changes sign:f = -f....
s.
If m ≤ n, then the matrix V has maximum rank (m) if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
all αi are distinct. A square Vandermonde matrix is thus invertible if and only if the αi are distinct; an explicit formula for the inverse is known.
Applications
The Vandermonde matrix evaluates a polynomial at a set of points; formally, it transforms coefficients of a polynomial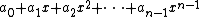 to the values the polynomial takes at the points 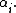The non-vanishing of the Vandermonde determinant for distinct points 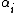shows that, for distinct points, the map from coefficients to values at those points is a one-to-one correspondence, and thus that the polynomial interpolation problem is solvable with unique solution; this result is called the unisolvence theorem.They are thus useful in polynomial interpolation
Polynomial interpolation
In numerical analysis, polynomial interpolation is the interpolation of a given data set by a polynomial: given some points, find a polynomial which goes exactly through these points.- Applications :...
, since solving the system of linear equations Vu = y for u with V an m × n Vandermonde matrix is equivalent to finding the coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s uj of the polynomial(s)
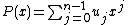
of degree ≤ n − 1 which has (have) the property
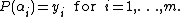
The Vandermonde matrix can easily be inverted in terms of Lagrange basis polynomials: each column is the coefficients of the Lagrange basis polynomial, with terms in increasing order going down. The resulting solution to the interpolation problem is called the Lagrange polynomial
Lagrange polynomial
In numerical analysis, Lagrange polynomials are used for polynomial interpolation. For a given set of distinct points x_j and numbers y_j, the Lagrange polynomial is the polynomial of the least degree that at each point x_j assumes the corresponding value y_j...
.
The Vandermonde determinant plays a central role in the Frobenius formula, which gives the character
Character theory
In mathematics, more specifically in group theory, the character of a group representation is a function on the group which associates to each group element the trace of the corresponding matrix....
of conjugacy class
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
es of representation
Representation theory of the symmetric group
In mathematics, the representation theory of the symmetric group is a particular case of the representation theory of finite groups, for which a concrete and detailed theory can be obtained. This has a large area of potential applications, from symmetric function theory to problems of quantum...
s of the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
.
When the values
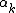range over powers of a finite fieldFinite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
, then the determinant
has a number of interesting properties: for example, in proving the properties of a BCH code
BCH code
In coding theory the BCH codes form a class of parameterised error-correcting codes which have been the subject of much academic attention in the last fifty years. BCH codes were invented in 1959 by Hocquenghem, and independently in 1960 by Bose and Ray-Chaudhuri...
.
Confluent Vandermonde matrices are used in Hermite interpolation
Hermite interpolation
In numerical analysis, Hermite interpolation, named after Charles Hermite, is a method of interpolating data points as a polynomial function. The generated Hermite polynomial is closely related to the Newton polynomial, in that both are derived from the calculation of divided differences.Unlike...
.
A commonly known special Vandermonde matrix is the discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
matrix (DFT matrix
DFT matrix
A DFT matrix is an expression of a discrete Fourier transform as a matrix multiplication.-Definition:An N-point DFT is expressed as an N-by-N matrix multiplication as X = W x, where x is the original input signal, and X is the DFT of the signal.The transformation W of size N\times N can be defined...
), where the numbers αi are chosen equal to the m different mth roots of unity
Root of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
.
The Vandermonde matrix diagonalizes a companion matrix.
See also
- Alternant matrixAlternant matrixIn linear algebra, an alternant matrix, is a matrix with a particular structure, in which successive columns have a particular function applied to their entries. An alternant determinant is the determinant of an alternant matrix...
- Lagrange polynomialLagrange polynomialIn numerical analysis, Lagrange polynomials are used for polynomial interpolation. For a given set of distinct points x_j and numbers y_j, the Lagrange polynomial is the polynomial of the least degree that at each point x_j assumes the corresponding value y_j...
- WronskianWronskianIn mathematics, the Wronskian is a determinant introduced by and named by . It is used in the study of differential equations, where it can sometimes be used to show that a set of solutions is linearly independent.-Definition:...
- List of matrices
- Moore determinant over a finite field