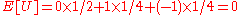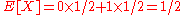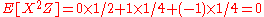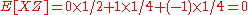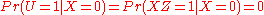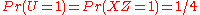Uncorrelated
Encyclopedia
In probability theory
and statistics
, two real-valued random variable
s are said to be uncorrelated if their covariance
is zero. Uncorrelatedness is by definition pairwise; i.e. to say that more than two random variables are uncorrelated simply means that any two of them are uncorrelated.
Uncorrelated random variables have a correlation coefficient
of zero, except in the trivial case when either variable has zero variance
(is a constant). In this case the correlation
is undefined.
In general, uncorrelatedness is not the same as orthogonality
, except in the special case where either X or Y has an expected value of 0. In this case, the covariance
is the expectation of the product, and X and Y are uncorrelated if and only if
E(XY) = E(X)E(Y).
If X and Y are independent
, then they are uncorrelated. However, not all uncorrelated variables are independent. For example, if X is a continuous random variable uniformly distributed
on [−1, 1] and Y = X2, then X and Y are uncorrelated even though X determines Y and a particular value of Y can be produced by only one or two values of X.
A set of two or more random variables is called uncorrelated if each pair of them are uncorrelated.
The claim is that U and X have zero covariance (and thus are uncorrelated), but are not independent.
Proof:
First note:
Now, by definition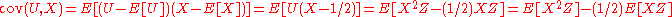
Therefore
A necessary condition for showing that U and X are independent is showing that for any number a and b, . We prove that this is not true. PIck a=1 and b=0.
. We prove that this is not true. PIck a=1 and b=0.
Thus so U and X are not independent.
so U and X are not independent.
Q.E.D.
.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, two real-valued random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s are said to be uncorrelated if their covariance
Covariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
is zero. Uncorrelatedness is by definition pairwise; i.e. to say that more than two random variables are uncorrelated simply means that any two of them are uncorrelated.
Uncorrelated random variables have a correlation coefficient
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
of zero, except in the trivial case when either variable has zero variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
(is a constant). In this case the correlation
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
is undefined.
In general, uncorrelatedness is not the same as orthogonality
Orthogonality
Orthogonality occurs when two things can vary independently, they are uncorrelated, or they are perpendicular.-Mathematics:In mathematics, two vectors are orthogonal if they are perpendicular, i.e., they form a right angle...
, except in the special case where either X or Y has an expected value of 0. In this case, the covariance
Covariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
is the expectation of the product, and X and Y are uncorrelated if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
E(XY) = E(X)E(Y).
If X and Y are independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
, then they are uncorrelated. However, not all uncorrelated variables are independent. For example, if X is a continuous random variable uniformly distributed
Uniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
on [−1, 1] and Y = X2, then X and Y are uncorrelated even though X determines Y and a particular value of Y can be produced by only one or two values of X.
A set of two or more random variables is called uncorrelated if each pair of them are uncorrelated.
Another example to prove that uncorrelated random variables are not necessarily independent
- Let X be a random variable that takes the value 0 with probability 1/2, and takes the value 1 with probability 1/2.
- Let Z be a random variable that takes the value -1 with probability 1/2, and takes the value 1 with probability 1/2.
- Let U be a random variable constructed as U=XZ.
The claim is that U and X have zero covariance (and thus are uncorrelated), but are not independent.
Proof:
First note:
Now, by definition
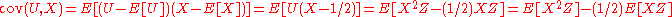
Therefore

A necessary condition for showing that U and X are independent is showing that for any number a and b,
 . We prove that this is not true. PIck a=1 and b=0.
. We prove that this is not true. PIck a=1 and b=0.
Thus
 so U and X are not independent.
so U and X are not independent.Q.E.D.
When uncorrelatedness implies independence
There are cases in which uncorrelatedness does imply independence. One of these cases is when both random variables are two-valued (which reduces to binomial distributions with n=1). See Binomial distribution#Covariance between two binomials for more information. Further, two jointly normally distributed random variables are independent if they are uncorrelated, although this does not hold for variables whose marginal distributions are normal and uncorrelated but whose joint distribution is not joint normal: see Normally distributed and uncorrelated does not imply independentNormally distributed and uncorrelated does not imply independent
In probability theory, two random variables being uncorrelated does not imply their independence. In some contexts, uncorrelatedness implies at least pairwise independence ....
.