
Twistor space
Encyclopedia
In mathematics
, twistor space is the complex vector space of solutions of the twistor equation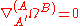 . It was described in the 1960s by Roger Penrose
. It was described in the 1960s by Roger Penrose
and MacCallum. According to Andrew Hodges, twistor space is useful for conceptualizing the way photons travel through space, using four complex numbers
. He also posits that twistor space may aid in understanding the asymmetry
of the weak nuclear force.
For Minkowski space, denoted the solutions to the twistor equation are of the form
the solutions to the twistor equation are of the form
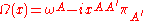
where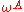 and
and  are two constant Weyl spinors and
are two constant Weyl spinors and 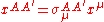 is a point in Minkowski space. This twistor space is a four dimensional complex vector space, whose points are denoted by
is a point in Minkowski space. This twistor space is a four dimensional complex vector space, whose points are denoted by 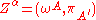 , and with a hermitian form
, and with a hermitian form
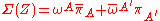
which is invariant under the group SU(2,2) which is a quadruple cover of the conformal group C(1,3) of compactified Minkowski spacetime.
Points in Minkowski space are related to subspaces of twistor space through the incidence relation
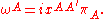
This incidence relation is preserved under an overall re-scaling of the twistor, so usually one works in projective twistor space, denoted PT which is isomorphic as a complex manifold to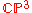 .
.
Given a point it is related to a line in projective twistor space where we can see the incidence relation as giving the linear embedding of
it is related to a line in projective twistor space where we can see the incidence relation as giving the linear embedding of
a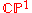 parametrized by
parametrized by  .
.
The geometric relation between projective twistor space and complexified compactified Minkowski space is the same as the relation between lines and two-planes in twistor space, more precisely twistor space is
T := C4. It has associated to it the double fibration of flag manifold
s P ←μ F ν→ M, where
In the above P stands for projective space
, G a Grassmannian
, and F a flag manifold
. The double fibration gives rise to two correspondences
, c := ν . μ−1 and c−1 := μ . ν−1.
M is embedded in P5 ~=~ P(Λ2T) by the Plücker embedding
and the image is the Klein quadric
.
: "the shortest path between two truths in the real domain passes through the complex domain." Therefore when studying R4 it might be valuable to identify it with C2. However, since there is no canonical way of doing so, instead all isomorphisms respecting orientation and metric between the two are considered. It turns out that complex projective 3-space P3(C) parametrizes such isomorphisms together with complex coordinates. Thus one complex coordinate describes the identification and the other two describe a point in R4. It turns out that vector bundles with self-dual connections on R4(instanton
s) correspond bijectively
to holomorphic bundles on complex projective 3-space P3(C).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, twistor space is the complex vector space of solutions of the twistor equation
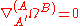 . It was described in the 1960s by Roger Penrose
. It was described in the 1960s by Roger PenroseRoger Penrose
Sir Roger Penrose OM FRS is an English mathematical physicist and Emeritus Rouse Ball Professor of Mathematics at the Mathematical Institute, University of Oxford and Emeritus Fellow of Wadham College...
and MacCallum. According to Andrew Hodges, twistor space is useful for conceptualizing the way photons travel through space, using four complex numbers
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
. He also posits that twistor space may aid in understanding the asymmetry
Asymmetry
Asymmetry is the absence of, or a violation of, symmetry.-In organisms:Due to how cells divide in organisms, asymmetry in organisms is fairly usual in at least one dimension, with biological symmetry also being common in at least one dimension....
of the weak nuclear force.
For Minkowski space, denoted
 the solutions to the twistor equation are of the form
the solutions to the twistor equation are of the form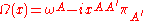
where
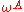 and
and  are two constant Weyl spinors and
are two constant Weyl spinors and 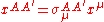 is a point in Minkowski space. This twistor space is a four dimensional complex vector space, whose points are denoted by
is a point in Minkowski space. This twistor space is a four dimensional complex vector space, whose points are denoted by 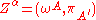 , and with a hermitian form
, and with a hermitian form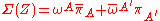
which is invariant under the group SU(2,2) which is a quadruple cover of the conformal group C(1,3) of compactified Minkowski spacetime.
Points in Minkowski space are related to subspaces of twistor space through the incidence relation
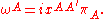
This incidence relation is preserved under an overall re-scaling of the twistor, so usually one works in projective twistor space, denoted PT which is isomorphic as a complex manifold to
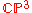 .
.Given a point
 it is related to a line in projective twistor space where we can see the incidence relation as giving the linear embedding of
it is related to a line in projective twistor space where we can see the incidence relation as giving the linear embedding ofa
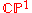 parametrized by
parametrized by  .
.The geometric relation between projective twistor space and complexified compactified Minkowski space is the same as the relation between lines and two-planes in twistor space, more precisely twistor space is
T := C4. It has associated to it the double fibration of flag manifold
Flag manifold
In mathematics, a generalized flag variety is a homogeneous space whose points are flags in a finite-dimensional vector space V over a field F. When F is the real or complex numbers, a generalized flag variety is a smooth or complex manifold, called a real or complex flag manifold...
s P ←μ F ν→ M, where
- projective twistor space
- P := F1(T) = P3(C) = P(C4)
- compactified complexified Minkowski spaceMinkowski spaceIn physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
- M := F2(T) = G2(C4) = G2,4(C)
- the correspondence space between P and M
- F := F1,2(T)
In the above P stands for projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
, G a Grassmannian
Grassmannian
In mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...
, and F a flag manifold
Flag manifold
In mathematics, a generalized flag variety is a homogeneous space whose points are flags in a finite-dimensional vector space V over a field F. When F is the real or complex numbers, a generalized flag variety is a smooth or complex manifold, called a real or complex flag manifold...
. The double fibration gives rise to two correspondences
Correspondence (mathematics)
In mathematics and mathematical economics, correspondence is a term with several related but not identical meanings.* In general mathematics, correspondence is an alternative term for a relation between two sets...
, c := ν . μ−1 and c−1 := μ . ν−1.
M is embedded in P5 ~=~ P(Λ2T) by the Plücker embedding
Plücker embedding
In mathematics, the Plücker embedding describes a method to realize the Grassmannian of all r-dimensional subspaces of a vector space V as a subvariety of the projective space of the rth exterior power of that vector space, P....
and the image is the Klein quadric
Klein quadric
The lines of a 3-dimensional projective space, S, can be viewed as points of a 5-dimensional projective space, T. In that 5-space, the points that represent a line in S lie on a hyperbolic quadric, Q known as the Klein quadric....
.
Rationale
In the (translated) words of Jacques HadamardJacques Hadamard
Jacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...
: "the shortest path between two truths in the real domain passes through the complex domain." Therefore when studying R4 it might be valuable to identify it with C2. However, since there is no canonical way of doing so, instead all isomorphisms respecting orientation and metric between the two are considered. It turns out that complex projective 3-space P3(C) parametrizes such isomorphisms together with complex coordinates. Thus one complex coordinate describes the identification and the other two describe a point in R4. It turns out that vector bundles with self-dual connections on R4(instanton
Instanton
An instanton is a notion appearing in theoretical and mathematical physics. Mathematically, a Yang–Mills instanton is a self-dual or anti-self-dual connection in a principal bundle over a four-dimensional Riemannian manifold that plays the role of physical space-time in non-abelian gauge theory...
s) correspond bijectively
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
to holomorphic bundles on complex projective 3-space P3(C).

