Topologist's sine curve
Encyclopedia
In the branch of mathematics
known as topology
, the topologist's sine curve is a topological space
with several interesting properties that make it an important textbook example.
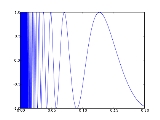
The topologist's sine curve can be defined as the graph
of the function sin(1/x) over the interval (0, 1], together with a point at the origin, under the topology induced
from the Euclidean plane.
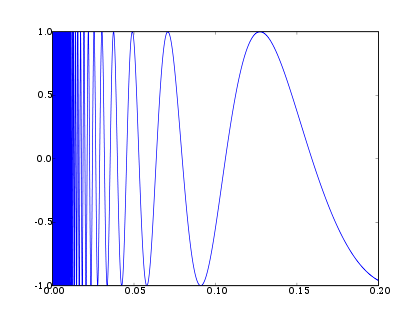As x approaches zero, 1/x approaches infinity at an increasing rate. This is why the frequency of the sine wave increases on the left side of the graph.
but neither locally connected
nor path connected. This is because it includes the point (0,0) but there is no way to link the function to the origin so as to make a path
.
T is the continuous image of a locally compact space (namely, let V be the space {−1} ∪ (0, 1] , and use the map f from V to T defined by f(−1) = (0,0) and f(x) = (x, sin(1/x)) for x > 0), but is not locally compact itself.
The topological dimension of T is 1.
The closed topologist's sine curve can be defined by taking the topologist's sine curve and adding its set of limit point
s,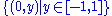
. This space is closed and bounded and so compact
by the Heine–Borel theorem
, but has similar properties to the topologist's sine curve—it too is connected but neither locally connected nor path-connected.
The extended topologist's sine curve can be defined by taking the closed topologist's sine curve and adding to it the set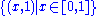
. It is arc connected but not locally connected
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
known as topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, the topologist's sine curve is a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
with several interesting properties that make it an important textbook example.
The topologist's sine curve can be defined as the graph
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
of the function sin(1/x) over the interval (0, 1], together with a point at the origin, under the topology induced
Subspace topology
In topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
from the Euclidean plane.
Image of the curve
Properties
The topologist's sine curve T is connectedConnected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
but neither locally connected
Locally connected space
In topology and other branches of mathematics, a topological space X islocally connected if every point admits a neighbourhood basis consisting entirely of open, connected sets.-Background:...
nor path connected. This is because it includes the point (0,0) but there is no way to link the function to the origin so as to make a path
Path (topology)
In mathematics, a path in a topological space X is a continuous map f from the unit interval I = [0,1] to XThe initial point of the path is f and the terminal point is f. One often speaks of a "path from x to y" where x and y are the initial and terminal points of the path...
.
T is the continuous image of a locally compact space (namely, let V be the space {−1} ∪ (0, 1
The topological dimension of T is 1.
Variations
Two variations of the topologist's sine curve have other interesting properties.The closed topologist's sine curve can be defined by taking the topologist's sine curve and adding its set of limit point
Limit point
In mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
s,
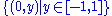. This space is closed and bounded and so compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
by the Heine–Borel theorem
Heine–Borel theorem
In the topology of metric spaces the Heine–Borel theorem, named after Eduard Heine and Émile Borel, states:For a subset S of Euclidean space Rn, the following two statements are equivalent:*S is closed and bounded...
, but has similar properties to the topologist's sine curve—it too is connected but neither locally connected nor path-connected.
The extended topologist's sine curve can be defined by taking the closed topologist's sine curve and adding to it the set
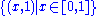. It is arc connected but not locally connectedLocally connected space
In topology and other branches of mathematics, a topological space X islocally connected if every point admits a neighbourhood basis consisting entirely of open, connected sets.-Background:...
.