
Path (topology)
Encyclopedia

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a path in a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X is a continuous map f from the unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
I = [0,1] to X
- f : I → X.
The initial point of the path is f(0) and the terminal point is f(1). One often speaks of a "path from x to y" where x and y are the initial and terminal points of the path. Note that a path is not just a subset of X which "looks like" a curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
, it also includes a parameterization
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
. For example, the maps f(x) = x and g(x) = x2 represent two different paths from 0 to 1 on the real line.
A loop
Loop (topology)
In mathematics, a loop in a topological space X is a path f from the unit interval I = [0,1] to X such that f = f...
in a space X based at x ∈ X is a path from x to x. A loop may be equally well regarded as a map f : I → X with f(0) = f(1) or as a continuous map from the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
S1 to X
- f : S1 → X.
This is because S1 may be regarded as a quotient
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
of I under the identification 0 ∼ 1. The set of all loops in X forms a space called the loop space of X.
A topological space for which there exists a path connecting any two points is said to be path-connected. Any space may be broken up into a set of path-connected components. The set of path-connected components of a space X is often denoted π0(X);.
One can also define paths and loops in pointed space
Pointed space
In mathematics, a pointed space is a topological space X with a distinguished basepoint x0 in X. Maps of pointed spaces are continuous maps preserving basepoints, i.e. a continuous map f : X → Y such that f = y0...
s, which are important in homotopy theory. If X is a topological space with basepoint x0, then a path in X is one whose initial point is x0. Likewise, a loop in X is one that is based at x0.
Homotopy of paths

Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
called homotopy theory. A homotopy
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
of paths makes precise the notion of continuously deforming a path while keeping its endpoints fixed.
Specifically, a homotopy of paths, or path-homotopy, in X is a family of paths ft : I → X indexed by I such that
- ft(0) = x0 and ft(1) = x1 are fixed.
- the map F : I × I → X given by F(s, t) = ft(s) is continuous.
The paths f0 and f1 connected by a homotopy are said to homotopic (or more precisely path-homotopic, to distinguish between the relation defined on all continuous functions between fixed spaces). One can likewise define a homotopy of loops keeping the base point fixed.
The relation of being homotopic is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on paths in a topological space. The equivalence class of a path f under this relation is called the homotopy class of f, often denoted [f].
Path composition
One can compose paths in a topological space in an obvious manner. Suppose f is a path from x to y and g is a path from y to z. The path fg is defined as the path obtained by first traversing f and then traversing g: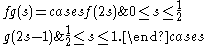
Clearly path composition is only defined when the terminal point of f coincides with the initial point of g. If one considers all loops based at a point x0, then path composition is a binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
.
Path composition, whenever defined, is not associative due to the difference in parametrization. However it is associative up to path-homotopy. That is, [(fg)h] = [f(gh)]. Path composition defines a group structure
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
on the set of homotopy classes of loops based at a point x0 in X. The resultant group is called the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of X based at x0, usually denoted π1(X,x0).
In situations calling for associativity of path composition "on the nose," a path in X may instead be defined as a continuous map from an interval [0,a] to X for any real a ≥ 0. A path f of this kind has a length |f| defined as a. Path composition is then defined as before with the following modification:
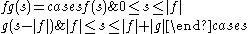
Whereas with the previous definition, f, g, and fg all have length 1 (the length of the domain of the map), this definition makes |fg| = |f| + |g|. What made associativity fail for the previous definition is that although (fg)h and f(gh) have the same length, namely 1, the midpoint of (fg)h occurred between g and h, whereas the midpoint of f(gh) occurred between f and g. With this modified definition (fg)h and f(gh) have the same length, namely |f|+|g|+|h|, and the same midpoint, found at (|f|+|g|+|h|)/2 in both (fg)h and f(gh); more generally they have the same parametrization throughout.
Fundamental groupoid
There is a categoricalCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
picture of paths which is sometimes useful. Any topological space X gives raise to a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
where the objects are the points of X and the morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s are the homotopy classes of paths. Since any morphism in this category is an isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
this category is a groupoid
Groupoid
In mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:...
, called the fundamental groupoid of X. Loops in this category are the endomorphism
Endomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
s (all of which are actually automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
s). The automorphism group of a point x0 in X is just the fundamental group based at X. More generally, one can define the fundamental groupoid on any subset A of X, using homotopy classes of paths joining points of A. This is convenient for the Van Kampen's Theorem.

