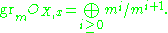
Tangent cone
Encyclopedia
In geometry
, the tangent cone is a generalization of the notion of the tangent space
to a manifold
to the case of certain spaces with singularities.
convex subset of a real vector space
V and ∂K be the boundary
of K. The solid tangent cone to K at a point x ∈ ∂K is the closure of the cone formed by all half-lines (or rays) emanating from x and intersecting K in at least one point y distinct from x. It is a convex cone
in V and can also be defined as the intersection of the closed half-space
s of V containing K and bounded by the supporting hyperplane
s of K at x. The boundary TK of the solid tangent cone is the tangent cone to K and ∂K at x. If this is an affine subspace of V then the point x is called a smooth point of ∂K and ∂K is said to be differentiable at x and TK is the ordinary tangent space
to ∂K at x.
.png) Let X be an affine algebraic variety embedded into the affine space kn, with the defining ideal I ⊂ k[x1,…,xn]. For any polynomial f, let in(f) be the homogeneous component of f of the lowest degree, the initial term of f, and let in(I) ⊂ k[x1,…,xn] be the homogeneous ideal which is formed by the initial terms in(f) for all f ∈ I, the initial ideal of I. The tangent cone to X at the origin is the Zariski closed subset of kn defined by the ideal in(I). By shifting the coordinate system, this definition extends to an arbitrary point of kn in place of the origin. The tangent cone serves as the extension of the notion of the tangent space to X at a regular point, where X most closely resembles a differentiable manifold
Let X be an affine algebraic variety embedded into the affine space kn, with the defining ideal I ⊂ k[x1,…,xn]. For any polynomial f, let in(f) be the homogeneous component of f of the lowest degree, the initial term of f, and let in(I) ⊂ k[x1,…,xn] be the homogeneous ideal which is formed by the initial terms in(f) for all f ∈ I, the initial ideal of I. The tangent cone to X at the origin is the Zariski closed subset of kn defined by the ideal in(I). By shifting the coordinate system, this definition extends to an arbitrary point of kn in place of the origin. The tangent cone serves as the extension of the notion of the tangent space to X at a regular point, where X most closely resembles a differentiable manifold
, to all of X. (The tangent cone at a point of kn that is not contained in X is empty.)
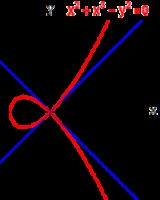
For example, the nodal curve
is singular at the origin, because both partial derivative
s of f(x, y) = y2 − x3 − x2 vanish at (0, 0). Thus the Zariski tangent space
to C at the origin is the whole plane, and has higher dimension than the curve itself (two versus one). On the other hand, the tangent cone is the union of the tangent lines to the two branches of C at the origin,
Its defining ideal is the principal ideal of k[x] generated by the initial term of f, namely y2 − x2 = 0.
The definition of the tangent cone can be extended to abstract algebraic varieties, and even to general Noetherian
schemes
. Let X be an algebraic variety
, x a point of X, and (OX,x ,m) be the local ring
of X at x. Then the tangent cone to X at x is the spectrum
of the associated graded ring of OX,x with respect to the m-adic filtration:
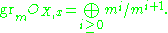
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the tangent cone is a generalization of the notion of the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
to a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
to the case of certain spaces with singularities.
Definition in convex geometry
Let K be a closedClosed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
convex subset of a real vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V and ∂K be the boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of K. The solid tangent cone to K at a point x ∈ ∂K is the closure of the cone formed by all half-lines (or rays) emanating from x and intersecting K in at least one point y distinct from x. It is a convex cone
Convex cone
In linear algebra, a convex cone is a subset of a vector space over an ordered field that is closed under linear combinations with positive coefficients.-Definition:...
in V and can also be defined as the intersection of the closed half-space
Half-space
In geometry, a half-space is either of the two parts into which a plane divides the three-dimensional euclidean space. More generally, a half-space is either of the two parts into which a hyperplane divides an affine space...
s of V containing K and bounded by the supporting hyperplane
Supporting hyperplane
Supporting hyperplane is a concept in geometry. A hyperplane divides a space into two half-spaces. A hyperplane is said to support a set S in Euclidean space \mathbb R^n if it meets both of the following:...
s of K at x. The boundary TK of the solid tangent cone is the tangent cone to K and ∂K at x. If this is an affine subspace of V then the point x is called a smooth point of ∂K and ∂K is said to be differentiable at x and TK is the ordinary tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
to ∂K at x.
Definition in algebraic geometry
.png)
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
, to all of X. (The tangent cone at a point of kn that is not contained in X is empty.)
For example, the nodal curve
is singular at the origin, because both partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s of f(x, y) = y2 − x3 − x2 vanish at (0, 0). Thus the Zariski tangent space
Zariski tangent space
In algebraic geometry, the Zariski tangent space is a construction that defines a tangent space at a point P on an algebraic variety V...
to C at the origin is the whole plane, and has higher dimension than the curve itself (two versus one). On the other hand, the tangent cone is the union of the tangent lines to the two branches of C at the origin,
Its defining ideal is the principal ideal of k[x] generated by the initial term of f, namely y2 − x2 = 0.
The definition of the tangent cone can be extended to abstract algebraic varieties, and even to general Noetherian
Noetherian
In mathematics, the adjective Noetherian is used to describe objects that satisfy an ascending or descending chain condition on certain kinds of subobjects; in particular,* Noetherian group, a group that satisfies the ascending chain condition on subgroups...
schemes
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
. Let X be an algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
, x a point of X, and (OX,x ,m) be the local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
of X at x. Then the tangent cone to X at x is the spectrum
Spectrum of a ring
In abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
of the associated graded ring of OX,x with respect to the m-adic filtration: