
Symbolic combinatorics
Encyclopedia
In mathematics, symbolic combinatorics is one of the many techniques of counting combinatorial objects
. It uses the internal structure of the objects to derive formulas for their generating function
s. This particular theory is due to Philippe Flajolet
and Robert Sedgewick
. This article describes the technique. For the underlying mathematics see fundamental theorem of combinatorial enumeration
.
 , containing a single object of size 0 (the neutral object, often denoted by
, containing a single object of size 0 (the neutral object, often denoted by  ), and one or more atomic classes
), and one or more atomic classes  , each containing a single object of size 1. Next, set-theoretic
, each containing a single object of size 1. Next, set-theoretic
relations involving various simple operations, such as disjoint union
s, products
, sets, sequence
s, and multiset
s define more complex classes in terms of the already defined classes. These relations may be recursive
. The elegance of symbolic combinatorics lies in that the set theoretic, or symbolic, relations translate directly into algebra
ic relations involving the generating functions.
In this article, we will follow the convention of using script uppercase letters to denote combinatorial classes and the corresponding plain letters for the generating functions (so the class has generating function
has generating function 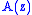 ).
).
There are two types of generating functions commonly used in symbolic combinatorics—ordinary generating functions, used for combinatorial classes of unlabelled objects, and exponential generating functions, used for classes of labelled objects.
It is trivial to show that the generating functions (either ordinary or exponential) for and
and  are
are 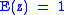 and
and 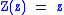 , respectively. The disjoint union is also simple — for disjoint sets
, respectively. The disjoint union is also simple — for disjoint sets  and
and  ,
,  implies
implies 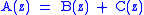 . The relations corresponding to other operations depend on whether we are talking about labelled or unlabelled structures (and ordinary or exponential generating functions).
. The relations corresponding to other operations depend on whether we are talking about labelled or unlabelled structures (and ordinary or exponential generating functions).
to disjoint unions is an important one; however, in the formal specification of symbolic combinatorics, it is too much trouble to keep track of which sets are disjoint. Instead, we make use of a construction that guarantees there is no intersection (be careful, however; this affects the semantics of the operation as well). In defining the combinatorial sum of two sets and
and  , we mark members of each set with a distinct marker, for example
, we mark members of each set with a distinct marker, for example  for members of
for members of  and
and  for members of
for members of  . The combinatorial sum is then:
. The combinatorial sum is then:
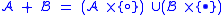
This is the operation that formally corresponds to addition.
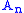 is defined as
is defined as
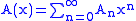
of two combinatorial classes and
and  is specified by defining the size of an ordered pair as the sum of the sizes of the elements in the pair. Thus we have for
is specified by defining the size of an ordered pair as the sum of the sizes of the elements in the pair. Thus we have for 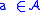 and
and 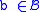 ,
,  . This should be a fairly intuitive definition. We now note that the number of elements in
. This should be a fairly intuitive definition. We now note that the number of elements in  of size n is
of size n is
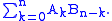
Using the definition of the OGF and some elementary algebra, we can show that
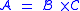 implies
implies 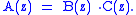
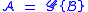 is defined as
is defined as
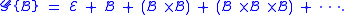
In other words, a sequence is the neutral element, or an element of , or an ordered pair, ordered triple, etc. This leads to the relation
, or an ordered pair, ordered triple, etc. This leads to the relation
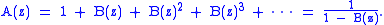
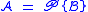 is defined as
is defined as
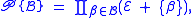
which leads to the relation
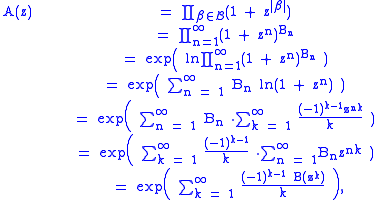
where the expansion
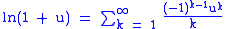
was used to go from line 4 to line 5.
 is a generalization of the set construction. In the set construction, each element can occur zero or one times. In a multiset, each element can appear an arbitrary number of times. Therefore,
is a generalization of the set construction. In the set construction, each element can occur zero or one times. In a multiset, each element can appear an arbitrary number of times. Therefore,
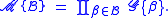
This leads to the relation
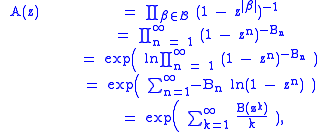
where, similar to the above set construction, we expand , swap the sums, and substitute for the OGF of
, swap the sums, and substitute for the OGF of  .
.
The derivations for these constructions are too complicated to show here. Here are the results:
in the plane, so that the order of the subtrees matters) is specified by the recursive
relation

In other words, a tree is a root node of size 1 and a sequence of subtrees. This gives
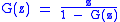
or
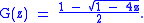
Another example (and a classic combinatorics problem) is integer partitions. First, define the class of positive integers , where the size of each integer is its value:
, where the size of each integer is its value:
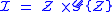
The OGF of is then
is then
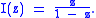
Now, define the set of partitions as
as

The OGF of is
is
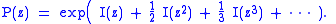
Unfortunately, there is no closed form for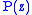 ; however, the OGF can be used to derive a recurrence relation
; however, the OGF can be used to derive a recurrence relation
, or, using more advanced methods of analytic combinatorics, calculate the asymptotic behavior of the counting sequence.
 . Note: some combinatorial classes are best specified as labelled structures or unlabelled structures, but some readily admit both specifications. A good example of labelled structures is the class of labelled graph
. Note: some combinatorial classes are best specified as labelled structures or unlabelled structures, but some readily admit both specifications. A good example of labelled structures is the class of labelled graph
s.
With labelled structures, an exponential generating function (EGF) is used. The EGF of a sequence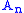 is defined as
is defined as
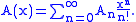
 .
.
For a pair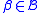 and
and 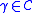 , we wish to combine the two structures into a single structure. In order for the result to be well labelled, this requires some relabelling of the atoms in
, we wish to combine the two structures into a single structure. In order for the result to be well labelled, this requires some relabelling of the atoms in 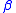 and
and  . We will restrict our attention to relabellings that are consistent with the order of the original labels. Note that there are still multiple ways to do the relabelling; thus, each pair of members determines not a single member in the product, but a set of new members. The details of this construction are found on the page of the Labelled enumeration theorem.
. We will restrict our attention to relabellings that are consistent with the order of the original labels. Note that there are still multiple ways to do the relabelling; thus, each pair of members determines not a single member in the product, but a set of new members. The details of this construction are found on the page of the Labelled enumeration theorem.
To aid this development, let us define a function, , that takes as its argument a (possibly weakly) labelled object
, that takes as its argument a (possibly weakly) labelled object  and relabels its atoms in an order-consistent way so that
and relabels its atoms in an order-consistent way so that 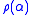 is well labelled. We then define the labelled product for two objects
is well labelled. We then define the labelled product for two objects  and
and 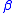 as
as
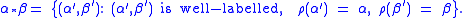
Finally, the labelled product of two classes and
and  is
is
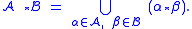
The EGF can be derived by noting that for objects of size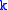 and
and  , there are
, there are 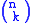 ways to do the relabelling. Therefore, the total number of objects of size
ways to do the relabelling. Therefore, the total number of objects of size  is
is
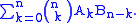
This binomial convolution relation for the terms is equivalent to multiplying the EGFs,
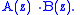
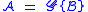 is defined similarly to the unlabelled case:
is defined similarly to the unlabelled case: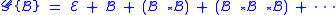
and again, as above,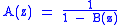
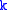 elements corresponds to exactly
elements corresponds to exactly  sequences. This is different from the unlabelled case, where some of the permutations may coincide. Thus for
sequences. This is different from the unlabelled case, where some of the permutations may coincide. Thus for 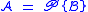 , we have
, we have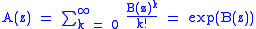
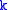 corresponds to
corresponds to 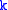 distinct sequences. Thus for
distinct sequences. Thus for 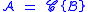 , we have
, we have
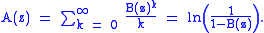

represent cycles of even and odd length, and sets of even and odd cardinality.
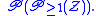
The decomposition

is used to study unsigned Stirling numbers of the first kind
, and in the derivation of
the statistics of random permutations
.
A detailed examination of the exponential generating functions associated to Stirling numbers may be found on the page on Stirling numbers and exponential generating functions
.
Enumerative combinatorics
Enumerative combinatorics is an area of combinatorics that deals with the number of ways that certain patterns can be formed. Two examples of this type of problem are counting combinations and counting permutations...
. It uses the internal structure of the objects to derive formulas for their generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
s. This particular theory is due to Philippe Flajolet
Philippe Flajolet
Philippe Flajolet was a French computer scientist.A former student of École Polytechnique, Philippe Flajolet received his Ph.D. in computer science from University Paris Diderot in 1973 and state doctorate from Paris-Sud 11 University in 1979...
and Robert Sedgewick
Robert Sedgewick
Robert Sedgewick may refer to:*Robert Sedgewick , computer scientist and author*Robert Sedgewick , Justice of the Supreme Court of Canada-Others:*Robert Sedgwick , American colonist...
. This article describes the technique. For the underlying mathematics see fundamental theorem of combinatorial enumeration
Fundamental theorem of combinatorial enumeration
The fundamental theorem of combinatorial enumeration is a theorem in combinatorics that solves the enumeration problem of labelled and unlabelled combinatorial classes.The unlabelled case is based on the Pólya enumeration theorem....
.
Procedure
Typically, one starts with the neutral class , containing a single object of size 0 (the neutral object, often denoted by
, containing a single object of size 0 (the neutral object, often denoted by  ), and one or more atomic classes
), and one or more atomic classes  , each containing a single object of size 1. Next, set-theoretic
, each containing a single object of size 1. Next, set-theoreticSet theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
relations involving various simple operations, such as disjoint union
Disjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
s, products
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
, sets, sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s, and multiset
Multiset
In mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
s define more complex classes in terms of the already defined classes. These relations may be recursive
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
. The elegance of symbolic combinatorics lies in that the set theoretic, or symbolic, relations translate directly into algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
ic relations involving the generating functions.
In this article, we will follow the convention of using script uppercase letters to denote combinatorial classes and the corresponding plain letters for the generating functions (so the class
 has generating function
has generating function 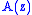 ).
).There are two types of generating functions commonly used in symbolic combinatorics—ordinary generating functions, used for combinatorial classes of unlabelled objects, and exponential generating functions, used for classes of labelled objects.
It is trivial to show that the generating functions (either ordinary or exponential) for
 and
and  are
are 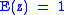 and
and 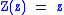 , respectively. The disjoint union is also simple — for disjoint sets
, respectively. The disjoint union is also simple — for disjoint sets  and
and  ,
,  implies
implies 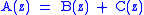 . The relations corresponding to other operations depend on whether we are talking about labelled or unlabelled structures (and ordinary or exponential generating functions).
. The relations corresponding to other operations depend on whether we are talking about labelled or unlabelled structures (and ordinary or exponential generating functions).Combinatorial sum
The restriction of unionsUnion (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
to disjoint unions is an important one; however, in the formal specification of symbolic combinatorics, it is too much trouble to keep track of which sets are disjoint. Instead, we make use of a construction that guarantees there is no intersection (be careful, however; this affects the semantics of the operation as well). In defining the combinatorial sum of two sets
 and
and  , we mark members of each set with a distinct marker, for example
, we mark members of each set with a distinct marker, for example  for members of
for members of  and
and  for members of
for members of  . The combinatorial sum is then:
. The combinatorial sum is then: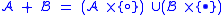
This is the operation that formally corresponds to addition.
Unlabelled structures
With unlabelled structures, an ordinary generating function (OGF) is used. The OGF of a sequence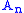 is defined as
is defined as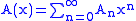
Product
The productCartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of two combinatorial classes
 and
and  is specified by defining the size of an ordered pair as the sum of the sizes of the elements in the pair. Thus we have for
is specified by defining the size of an ordered pair as the sum of the sizes of the elements in the pair. Thus we have for 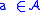 and
and 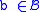 ,
,  . This should be a fairly intuitive definition. We now note that the number of elements in
. This should be a fairly intuitive definition. We now note that the number of elements in  of size n is
of size n is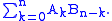
Using the definition of the OGF and some elementary algebra, we can show that
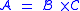 implies
implies 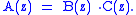
Sequence
The sequence construction, denoted by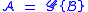 is defined as
is defined as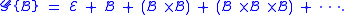
In other words, a sequence is the neutral element, or an element of
 , or an ordered pair, ordered triple, etc. This leads to the relation
, or an ordered pair, ordered triple, etc. This leads to the relation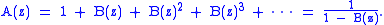
Set
The set (or powerset) construction, denoted by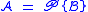 is defined as
is defined as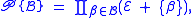
which leads to the relation
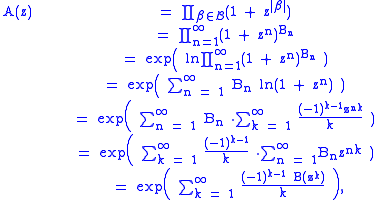
where the expansion
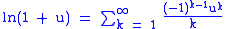
was used to go from line 4 to line 5.
Multiset
The multiset construction, denoted is a generalization of the set construction. In the set construction, each element can occur zero or one times. In a multiset, each element can appear an arbitrary number of times. Therefore,
is a generalization of the set construction. In the set construction, each element can occur zero or one times. In a multiset, each element can appear an arbitrary number of times. Therefore,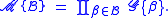
This leads to the relation
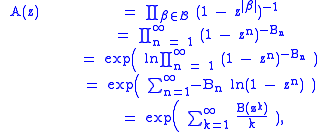
where, similar to the above set construction, we expand
 , swap the sums, and substitute for the OGF of
, swap the sums, and substitute for the OGF of  .
.Other elementary constructions
Other important elementary constructions are:- the cycle construction (
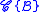 ), like sequences except that cyclic rotations are not considered distinct
), like sequences except that cyclic rotations are not considered distinct - pointing (
 ), in which each member of
), in which each member of  is augmented by a neutral (zero size) pointer to one of its atoms
is augmented by a neutral (zero size) pointer to one of its atoms - substitution (
 ), in which each atom in a member of
), in which each atom in a member of  is replaced by a member of
is replaced by a member of  .
.
The derivations for these constructions are too complicated to show here. Here are the results:
| Construction | Generating function |
|---|---|
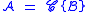 |
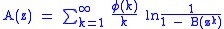 (where (where 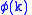 is the Euler totient function) is the Euler totient function) |
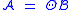 |
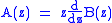 |
 |
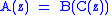 |
Examples
Many combinatorial classes can be built using these elementary constructions. For example, the class of plane trees (that is, trees embeddedEmbedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
in the plane, so that the order of the subtrees matters) is specified by the recursive
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
relation

In other words, a tree is a root node of size 1 and a sequence of subtrees. This gives
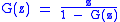
or
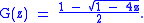
Another example (and a classic combinatorics problem) is integer partitions. First, define the class of positive integers
 , where the size of each integer is its value:
, where the size of each integer is its value: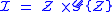
The OGF of
 is then
is then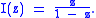
Now, define the set of partitions
 as
as
The OGF of
 is
is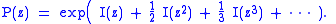
Unfortunately, there is no closed form for
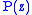 ; however, the OGF can be used to derive a recurrence relation
; however, the OGF can be used to derive a recurrence relationRecurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
, or, using more advanced methods of analytic combinatorics, calculate the asymptotic behavior of the counting sequence.
Labelled structures
An object is weakly labelled if each of its atoms has a nonnegative integer label, and each of these labels is distinct. An object is (strongly or well) labelled, if furthermore, these labels comprise the consecutive integers . Note: some combinatorial classes are best specified as labelled structures or unlabelled structures, but some readily admit both specifications. A good example of labelled structures is the class of labelled graph
. Note: some combinatorial classes are best specified as labelled structures or unlabelled structures, but some readily admit both specifications. A good example of labelled structures is the class of labelled graphGraph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
s.
With labelled structures, an exponential generating function (EGF) is used. The EGF of a sequence
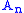 is defined as
is defined as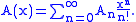
Product
For labelled structures, we must use a different definition for product than for unlabelled structures. In fact, if we simply used the cartesian product, the resulting structures would not even be well labelled. Instead, we use the so-called labelled product, denoted .
.For a pair
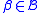 and
and 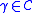 , we wish to combine the two structures into a single structure. In order for the result to be well labelled, this requires some relabelling of the atoms in
, we wish to combine the two structures into a single structure. In order for the result to be well labelled, this requires some relabelling of the atoms in 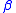 and
and  . We will restrict our attention to relabellings that are consistent with the order of the original labels. Note that there are still multiple ways to do the relabelling; thus, each pair of members determines not a single member in the product, but a set of new members. The details of this construction are found on the page of the Labelled enumeration theorem.
. We will restrict our attention to relabellings that are consistent with the order of the original labels. Note that there are still multiple ways to do the relabelling; thus, each pair of members determines not a single member in the product, but a set of new members. The details of this construction are found on the page of the Labelled enumeration theorem.To aid this development, let us define a function,
 , that takes as its argument a (possibly weakly) labelled object
, that takes as its argument a (possibly weakly) labelled object  and relabels its atoms in an order-consistent way so that
and relabels its atoms in an order-consistent way so that 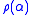 is well labelled. We then define the labelled product for two objects
is well labelled. We then define the labelled product for two objects  and
and 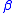 as
as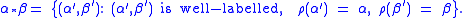
Finally, the labelled product of two classes
 and
and  is
is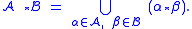
The EGF can be derived by noting that for objects of size
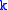 and
and  , there are
, there are 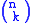 ways to do the relabelling. Therefore, the total number of objects of size
ways to do the relabelling. Therefore, the total number of objects of size  is
is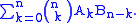
This binomial convolution relation for the terms is equivalent to multiplying the EGFs,
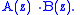
Sequence
The sequence construction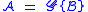 is defined similarly to the unlabelled case:
is defined similarly to the unlabelled case: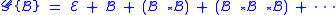
and again, as above,
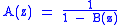
Set
In labelled structures, a set of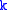 elements corresponds to exactly
elements corresponds to exactly  sequences. This is different from the unlabelled case, where some of the permutations may coincide. Thus for
sequences. This is different from the unlabelled case, where some of the permutations may coincide. Thus for 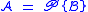 , we have
, we have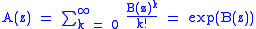
Cycle
Cycles are also easier than in the unlabelled case. A cycle of length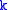 corresponds to
corresponds to 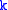 distinct sequences. Thus for
distinct sequences. Thus for 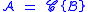 , we have
, we have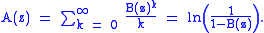
Other elementary constructions
The operators
represent cycles of even and odd length, and sets of even and odd cardinality.
Examples
Stirling numbers of the second kind may be derived and analyzed using the structural decomposition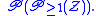
The decomposition

is used to study unsigned Stirling numbers of the first kind
Stirling numbers of the first kind
In mathematics, Stirling numbers of the first kind, together with the Stirling numbers of the second kind, are the two types of Stirling numbers. They commonly occur in combinatorics, where they appear in the study of permutations. The Stirling numbers of the first and second kind can be...
, and in the derivation of
the statistics of random permutations
Random permutation statistics
The statistics of random permutations, such as the cycle structure of a random permutation are of fundamental importance in the analysis of algorithms, especially of sorting algorithms, which operate on random permutations. Suppose, for example, that we are using quickselect to select a random...
.
A detailed examination of the exponential generating functions associated to Stirling numbers may be found on the page on Stirling numbers and exponential generating functions
Stirling numbers and exponential generating functions
The use of exponential generating functions to study the properties of Stirling numbers is a classical exercise in combinatorics and possibly the canonical example of how symbolic combinatorics, the method that encapsulates the fundamental theorem of combinatorial enumeration, is used...
.
External links
- Philippe Flajolet and Robert Sedgewick, Analytic Combinatorics: Symbolic Combinatorics.

