In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the concepts of subderivative, subgradient, and subdifferential arise in convex analysis

Convex analysis

Convex analysis is the branch of mathematics devoted to the study of properties of convex functions and convex sets, often with applications in convex minimization, a subdomain of optimization theory....

, that is, in the study of convex functions, often in connection to convex optimization.

Let f:I→R be a real

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

-valued convex function defined on an open interval of the real line. Such a function need not be differentiable

Derivative

In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...

 at all points: For example, the absolute value

Absolute value

In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...

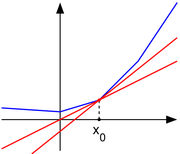
 function f(x)=|x| is nondifferentiable when x=0. However, as seen in the picture on the right, for any x₀ in the domain of the function one can draw a line which goes through the point (x₀, f(x₀)) and which is everywhere either touching or below the graph of f. The slope

Slope

In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....

 of such a line is called a subderivative (because the line is under the graph of f).

Definition

Rigorously, a subderivative of a function f:I→R at a point x₀ in the open interval I is a real number c such that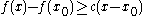
for all x in I. One may show that the set of subderivatives at x₀ for a convex function is a nonempty

Empty set

In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...

 closed interval [a, b], where a and b are the one-sided limit

One-sided limit

In calculus, a one-sided limit is either of the two limits of a function f of a real variable x as x approaches a specified point either from below or from above...

s



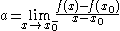
which are guaranteed to exist and satisfy a ≤ b.

The set [a, b] of all subderivatives is called the subdifferential of the function f at x₀. If f is convex and its subdifferential at 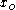contains exactly one subderivative, then f is differentiable at .

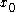Examples

Consider the function f(x)=|x| which is convex. Then, the subdifferential at the origin is the interval [−1, 1]. The subdifferential at any point x₀<0 is the singleton set {−1}, while the subdifferential at any point x₀>0 is the singleton {1}.

Properties

• A convex function f:I→R is differentiable at x₀ if and only if
  If and only if
  In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
  
   the subdifferential is made up of only one point, which is the derivative at x₀.

• A point x₀ is a global minimum of a convex function f if and only if zero is contained in the subdifferential, that is, in the figure above, one may draw a horizontal "subtangent line" to the graph of f at (x₀, f(x₀)). This last property is a generalization of the fact that the derivative of a function differentiable at a local minimum is zero.

The subgradient

The concepts of subderivative and subdifferential can be generalized to functions of several variables. If f:U→ R is a real-valued convex function defined on a convex

Convex set

In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...

 open set

Open set

The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...

 in the Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

 Rⁿ, a vector v in that space is called a subgradient at a point x₀ in U if for any x in U one has
where the dot denotes the dot product

Dot product

In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...

.
The set of all subgradients at x₀ is called the subdifferential at x₀ and is denoted ∂f(x₀). The subdifferential is always a nonempty convex compact set.

These concepts generalize further to convex functions f:U→ R on a convex set

Convex set

In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...

 in a locally convex space V. A functional v^∗ in the dual space

Dual space

In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...

 V^∗ is called subgradient at x₀ in U if
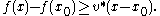
The set of all subgradients at x₀ is called the subdifferential at x₀ and is again denoted ∂f(x₀). The subdifferential is always a convex closed set

Closed set

In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...

. It can be an empty set; consider for example an unbounded operator

Unbounded operator

In mathematics, more specifically functional analysis and operator theory, the notion of unbounded operator provides an abstract framework for dealing with differential operators, unbounded observables in quantum mechanics, and other cases....

, which is convex, but has no subgradient. If f is continuous, the subdifferential is nonempty.