
Stone's theorem on one-parameter unitary groups
Encyclopedia
In mathematics
, Stone's theorem on one-parameter
unitary group
s is a basic theorem of functional analysis
which establishes a one-to-one correspondence between self-adjoint operator
s on a Hilbert space
H and one-parameter families of unitary operators
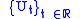
which are strongly continuous
, that is
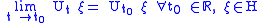
and are homomorphisms:
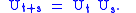
Such one-parameter families are ordinarily referred to as strongly continuous one-parameter unitary groups. The theorem was proved by . showed that the condition that Ut is strongly continuous can be relaxed to say that it is weakly measurable, at least when the Hilbert space is separable.
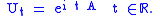
Conversely, let A be a self-adjoint operator on a Hilbert space H. Then
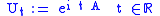
is a strongly continuous one-parameter family of unitary operators.
The infinitesimal generator of {Ut}t is the operator . This mapping is a bijective correspondence. A will be a bounded operator iff
. This mapping is a bijective correspondence. A will be a bounded operator iff
the operator-valued function is norm
is norm
continuous.
Stone's theorem can be recast using the language of Fourier transform
. The real line R is a locally compact abelian group. Nondegenerate representations of the group C*-algebra
C*(R) is in one-to-one correspondence with strongly continuous unitary representations R, i.e. strongly continuous one-parameter family of unitary operators. On the other hand, the Fourier transform is a *-isomorphism between C*(R) and C0(R), the C*-algebra of continuous functions on the line vanishing at infinity. So there is a one-to-one correspondence between strongly continuous one-parameter unitary groups and representations of C0(R). Since every representation of C0(R) corresponds to a self-adjoint operator, Stone's theorem holds.
The precise definition of C*(R) is as follows. Form the convolution algebra on Cc(R), the continuous functions of compact support, where the multiplication is convolution
. The completion of this algebra in the L1 norm is a *-algebra, denoted by L1(R). C*(R) is then defined to be the enveloping C*-algebra of L1(R), i.e. its completion in the largest possible C*-norm. It is not trivial that C*(R) is isomorphic to C0(R), under the Fourier transform. A result in this direction is the Riemann–Lebesgue lemma, which says the Fourier transform maps L1(R) to C0(R).

is a one-parameter unitary group of unitary operators; the infinitesimal generator of this family is an extension
of the differential operator
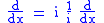
defined on the space of complex-valued continuously differentiable functions of compact support on R. Thus
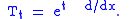
In other words, motion on the line is generated by the momentum operator
.
. For instance, given an isolated quantum mechanical system, with Hilbert space of states H, time evolution
is a strongly continuous one-parameter unitary group on H. The infinitesimal generator of this group is the system Hamiltonian.
generalizes Stone's theorem to a pair of self-adjoint operators, Q, P satisfying the canonical commutation relation
, and shows that these are all unitarily equivalent to the position operator
and momentum operator
on L2(R).
The Hille–Yosida theorem
generalizes Stone's theorem to strongly continuous one-parameter semigroups of contraction
s on Banach space
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Stone's theorem on one-parameter
One-parameter group
In mathematics, a one-parameter group or one-parameter subgroup usually means a continuous group homomorphismfrom the real line R to some other topological group G...
unitary group
Unitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
s is a basic theorem of functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
which establishes a one-to-one correspondence between self-adjoint operator
Self-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
s on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
H and one-parameter families of unitary operators
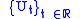
which are strongly continuous
Strong operator topology
In functional analysis, a branch of mathematics, the strong operator topology, often abbreviated SOT, is the weakest locally convex topology on the set of bounded operators on a Hilbert space such that the evaluation map sending an operator T to the real number \|Tx\| is continuous for each vector...
, that is
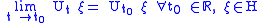
and are homomorphisms:
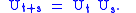
Such one-parameter families are ordinarily referred to as strongly continuous one-parameter unitary groups. The theorem was proved by . showed that the condition that Ut is strongly continuous can be relaxed to say that it is weakly measurable, at least when the Hilbert space is separable.
Formal statement
Let U be a strongly continuous 1-parameter unitary group, then there exists a unique self-adjoint operator A such that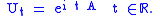
Conversely, let A be a self-adjoint operator on a Hilbert space H. Then
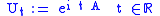
is a strongly continuous one-parameter family of unitary operators.
The infinitesimal generator of {Ut}t is the operator
 . This mapping is a bijective correspondence. A will be a bounded operator iff
. This mapping is a bijective correspondence. A will be a bounded operator iffIFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
the operator-valued function
 is norm
is normNorm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
continuous.
Stone's theorem can be recast using the language of Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
. The real line R is a locally compact abelian group. Nondegenerate representations of the group C*-algebra
Group algebra
In mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...
C*(R) is in one-to-one correspondence with strongly continuous unitary representations R, i.e. strongly continuous one-parameter family of unitary operators. On the other hand, the Fourier transform is a *-isomorphism between C*(R) and C0(R), the C*-algebra of continuous functions on the line vanishing at infinity. So there is a one-to-one correspondence between strongly continuous one-parameter unitary groups and representations of C0(R). Since every representation of C0(R) corresponds to a self-adjoint operator, Stone's theorem holds.
The precise definition of C*(R) is as follows. Form the convolution algebra on Cc(R), the continuous functions of compact support, where the multiplication is convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
. The completion of this algebra in the L1 norm is a *-algebra, denoted by L1(R). C*(R) is then defined to be the enveloping C*-algebra of L1(R), i.e. its completion in the largest possible C*-norm. It is not trivial that C*(R) is isomorphic to C0(R), under the Fourier transform. A result in this direction is the Riemann–Lebesgue lemma, which says the Fourier transform maps L1(R) to C0(R).
Example
The family of translation operators
is a one-parameter unitary group of unitary operators; the infinitesimal generator of this family is an extension
Extensions of symmetric operators
In functional analysis, one is interested in extensions of symmetric operators acting on a Hilbert space. Of particular importance is the existence, and sometimes explicit constructions, of self-adjoint extensions. This problem arises, for example, when one needs to specify domains of...
of the differential operator
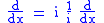
defined on the space of complex-valued continuously differentiable functions of compact support on R. Thus
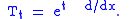
In other words, motion on the line is generated by the momentum operator
Momentum operator
In quantum mechanics, momentum is defined as an operator on the wave function. The Heisenberg uncertainty principle defines limits on how accurately the momentum and position of a single observable system can be known at once...
.
Applications
Stone's theorem has numerous applications in quantum mechanicsQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. For instance, given an isolated quantum mechanical system, with Hilbert space of states H, time evolution
Time evolution
Time evolution is the change of state brought about by the passage of time, applicable to systems with internal state . In this formulation, time is not required to be a continuous parameter, but may be discrete or even finite. In classical physics, time evolution of a collection of rigid bodies...
is a strongly continuous one-parameter unitary group on H. The infinitesimal generator of this group is the system Hamiltonian.
Generalizations
The Stone–von Neumann theoremStone–von Neumann theorem
In mathematics and in theoretical physics, the Stone–von Neumann theorem is any one of a number of different formulations of the uniqueness of the canonical commutation relations between position and momentum operators...
generalizes Stone's theorem to a pair of self-adjoint operators, Q, P satisfying the canonical commutation relation
Canonical commutation relation
In physics, the canonical commutation relation is the relation between canonical conjugate quantities , for example:[x,p_x] = i\hbar...
, and shows that these are all unitarily equivalent to the position operator
Position operator
In quantum mechanics, the position operator is the operator that corresponds to the position observable of a particle. Consider, for example, the case of a spinless particle moving on a line. The state space for such a particle is L2, the Hilbert space of complex-valued and square-integrable ...
and momentum operator
Momentum operator
In quantum mechanics, momentum is defined as an operator on the wave function. The Heisenberg uncertainty principle defines limits on how accurately the momentum and position of a single observable system can be known at once...
on L2(R).
The Hille–Yosida theorem
Hille–Yosida theorem
In functional analysis, the Hille–Yosida theorem characterizes the generators of strongly continuous one-parameter semigroups of linear operators on Banach spaces. It is sometimes stated for the special case of contraction semigroups, with the general case being called the Feller–Miyadera–Phillips...
generalizes Stone's theorem to strongly continuous one-parameter semigroups of contraction
Contraction (operator theory)
In operator theory, a bounded operator T: X → Y between normed vector spaces X and Y is said to be a contraction if its operator norm ||T|| ≤ 1. Every bounded operator becomes a contraction after suitable scaling...
s on Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s.

