Boltzmann distribution
Encyclopedia
In chemistry
, physics
, and mathematics
, the Boltzmann distribution is a certain distribution function
or probability measure
for the distribution of the states of a system. It underpins the concept of the canonical ensemble
, providing its underlying distribution. A special case of the Boltzmann distribution, used for describing the velocities of particles of a gas, is the Maxwell–Boltzmann distribution. In more general mathematical settings, the Boltzmann distribution is also known as the Gibbs measure
.
The Boltzmann distribution for the fractional number of particles Ni / N occupying a set of states i possessing energy Ei is:
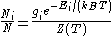
where
is the Boltzmann constant, T is temperature (assumed to be a well-defined quantity), 
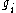is the degeneracy (meaning, the number of levels having energy 
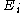; sometimes, the more general 'states' are used instead of levels, to avoid using degeneracy in the equation), N is the total number of particles and Z(T) is the partition function
.
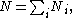
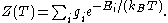
Alternatively, for a single system at a well-defined temperature, it gives the probability
that the system is in the specified state. The Boltzmann distribution applies only to particles at a high enough temperature and low enough density that quantum effects can be ignored, and the particles are obeying Maxwell–Boltzmann statistics
. (See that article for a derivation of the Boltzmann distribution.)
The Boltzmann distribution is often expressed in terms of β = 1/kT where β is referred to as thermodynamic beta. The term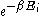
or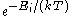 
, which gives the (unnormalised) relative probability of a state, is called the Boltzmann factor
and appears often in the study of physics and chemistry.
When the energy is simply the kinetic energy
of the particle
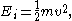
then the distribution correctly gives the Maxwell–Boltzmann distribution of gas molecule speeds, previously predicted by Maxwell
in 1859. The Boltzmann distribution is, however, much more general. For example, it also predicts the variation of the particle density in a gravitational field with height, if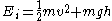
. In fact the distribution applies whenever quantum considerations can be ignored.
In some cases, a continuum approximation can be used. If there are g(E) dE states with energy E to E + dE, then the Boltzmann distribution predicts a probability distribution for the energy:
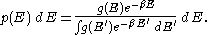
Then g(E) is called the density of states
if the energy spectrum is continuous.
Classical particles with this energy distribution are said to obey Maxwell–Boltzmann statistics
.
In the classical limit, i.e. at large values of
or at small density of states
— when wave functions of particles practically do not overlap — both the Bose–Einstein
or Fermi–Dirac distribution become the Boltzmann distribution.
Chemistry
Chemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....
, physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, and mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Boltzmann distribution is a certain distribution function
Distribution function
In molecular kinetic theory in physics, a particle's distribution function is a function of seven variables, f, which gives the number of particles per unit volume in phase space. It is the number of particles per unit volume having approximately the velocity near the place and time...
or probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
for the distribution of the states of a system. It underpins the concept of the canonical ensemble
Canonical ensemble
The canonical ensemble in statistical mechanics is a statistical ensemble representing a probability distribution of microscopic states of the system...
, providing its underlying distribution. A special case of the Boltzmann distribution, used for describing the velocities of particles of a gas, is the Maxwell–Boltzmann distribution. In more general mathematical settings, the Boltzmann distribution is also known as the Gibbs measure
Gibbs measure
In mathematics, the Gibbs measure, named after Josiah Willard Gibbs, is a probability measure frequently seen in many problems of probability theory and statistical mechanics. It is the measure associated with the Boltzmann distribution, and generalizes the notion of the canonical ensemble...
.
The Boltzmann distribution for the fractional number of particles Ni / N occupying a set of states i possessing energy Ei is:
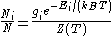
where
is the Boltzmann constant, T is temperature (assumed to be a well-defined quantity), 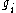is the degeneracy (meaning, the number of levels having energy 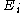; sometimes, the more general 'states' are used instead of levels, to avoid using degeneracy in the equation), N is the total number of particles and Z(T) is the partition functionPartition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
.
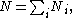
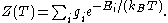
Alternatively, for a single system at a well-defined temperature, it gives the probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
that the system is in the specified state. The Boltzmann distribution applies only to particles at a high enough temperature and low enough density that quantum effects can be ignored, and the particles are obeying Maxwell–Boltzmann statistics
Maxwell–Boltzmann statistics
In statistical mechanics, Maxwell–Boltzmann statistics describes the statistical distribution of material particles over various energy states in thermal equilibrium, when the temperature is high enough and density is low enough to render quantum effects negligible.The expected number of particles...
. (See that article for a derivation of the Boltzmann distribution.)
The Boltzmann distribution is often expressed in terms of β = 1/kT where β is referred to as thermodynamic beta. The term
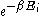or 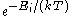, which gives the (unnormalised) relative probability of a state, is called the Boltzmann factorBoltzmann factor
In physics, the Boltzmann factor is a weighting factor that determines the relative probability of a particle to be in a state i in a multi-state system in thermodynamic equilibrium at temperature T...
and appears often in the study of physics and chemistry.
When the energy is simply the kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
of the particle
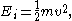
then the distribution correctly gives the Maxwell–Boltzmann distribution of gas molecule speeds, previously predicted by Maxwell
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
in 1859. The Boltzmann distribution is, however, much more general. For example, it also predicts the variation of the particle density in a gravitational field with height, if
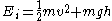. In fact the distribution applies whenever quantum considerations can be ignored.In some cases, a continuum approximation can be used. If there are g(E) dE states with energy E to E + dE, then the Boltzmann distribution predicts a probability distribution for the energy:
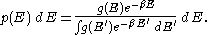
Then g(E) is called the density of states
Density of states
In solid-state and condensed matter physics, the density of states of a system describes the number of states per interval of energy at each energy level that are available to be occupied by electrons. Unlike isolated systems, like atoms or molecules in gas phase, the density distributions are not...
if the energy spectrum is continuous.
Classical particles with this energy distribution are said to obey Maxwell–Boltzmann statistics
Maxwell–Boltzmann statistics
In statistical mechanics, Maxwell–Boltzmann statistics describes the statistical distribution of material particles over various energy states in thermal equilibrium, when the temperature is high enough and density is low enough to render quantum effects negligible.The expected number of particles...
.
In the classical limit, i.e. at large values of
or at small density of statesDensity of states
In solid-state and condensed matter physics, the density of states of a system describes the number of states per interval of energy at each energy level that are available to be occupied by electrons. Unlike isolated systems, like atoms or molecules in gas phase, the density distributions are not...
— when wave functions of particles practically do not overlap — both the Bose–Einstein
Bose–Einstein statistics
In statistical mechanics, Bose–Einstein statistics determines the statistical distribution of identical indistinguishable bosons over the energy states in thermal equilibrium.-Concept:...
or Fermi–Dirac distribution become the Boltzmann distribution.
External links
See also
- Partition function (mathematics)Partition function (mathematics)The partition function or configuration integral, as used in probability theory, information science and dynamical systems, is an abstraction of the definition of a partition function in statistical mechanics. It is a special case of a normalizing constant in probability theory, for the Boltzmann...
- Gibbs measureGibbs measureIn mathematics, the Gibbs measure, named after Josiah Willard Gibbs, is a probability measure frequently seen in many problems of probability theory and statistical mechanics. It is the measure associated with the Boltzmann distribution, and generalizes the notion of the canonical ensemble...