
Conditional probability
Encyclopedia
In probability theory, the "conditional probability of  given
given 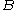 " is the probability of
" is the probability of  if
if 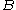 is known to occur. It is commonly notated
is known to occur. It is commonly notated 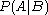 , and sometimes
, and sometimes  . (The vertical line should not be mistaken for logical OR.)
. (The vertical line should not be mistaken for logical OR.)  can be visualised as the probability of event
can be visualised as the probability of event  when the sample space is restricted to event
when the sample space is restricted to event 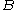 . Mathematically, it is defined for
. Mathematically, it is defined for  as
as
Formally,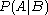 is defined as the probability of
is defined as the probability of 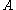 according to a new probability function on the sample space, such that outcomes not in
according to a new probability function on the sample space, such that outcomes not in 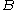 have probability 0 and that it is consistent with all original probability measures
have probability 0 and that it is consistent with all original probability measures
. The above definition follows (see Formal derivation).
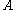 and
and  in the same probability space
in the same probability space
with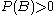 , the conditional probability of
, the conditional probability of 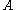 given
given  is defined as the quotient
is defined as the quotient
of the unconditional joint probability of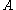 and
and 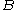 , and the unconditional probability
, and the unconditional probability
of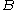 :
:
 , then the simple definition of
, then the simple definition of  is undefined. However, it is possible to define a conditional probability with respect to a σ-algebra of such events (such as those arising from a continuous random variable).
is undefined. However, it is possible to define a conditional probability with respect to a σ-algebra of such events (such as those arising from a continuous random variable).
For example, if X and Y are non-degenerate and jointly continuous random variables with density ƒX,Y(x, y) then, if B has positive measure
,
The case where B has zero measure can only be dealt with directly in the case that B={y0}, representing a single point, in which case
If A has measure zero then the conditional probability is zero. An indication of why the more general case of zero measure cannot be dealt with in a similar way can be seen by noting that the limit, as all δyi approach zero, of
depends on their relationship as they approach zero. See conditional expectation
for more information.
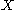 be a random variable taking some value from
be a random variable taking some value from  . Let
. Let  be an event. The probability of
be an event. The probability of 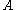 given
given  is defined as
is defined as

Note that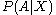 and
and  are now both random variable
are now both random variable
s. From the law of total probability
, the expected value
of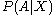 is equal to the unconditional probability
is equal to the unconditional probability
of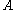 .
.
.
Suppose we roll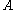 and
and  . What is the probability that
. What is the probability that  ? Table 1 shows the sample space.
? Table 1 shows the sample space. 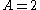 in 6 of the 36 outcomes, so
in 6 of the 36 outcomes, so 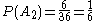 .
.
Suppose however that somebody else rolls the dice in secret, revealing only that . Table 2 shows that
. Table 2 shows that 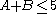 for 10 outcomes.
for 10 outcomes.  in 3 of these. The probability that
in 3 of these. The probability that 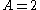 given that
given that  is therefore
is therefore  . This is a conditional probability, because it has a condition that limits the sample space. In more compact notation,
. This is a conditional probability, because it has a condition that limits the sample space. In more compact notation, 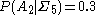 .
.
 and
and  are statistically independent
are statistically independent
, the occurrence of does not affect the probability of
does not affect the probability of 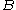 , and vice versa. That is,
, and vice versa. That is,

 .
.
Using the definition of conditional probability, it follows from either formula that

This is the definition of statistical independence
. This form is the preferred definition, as it is symmetrical in and
and  , and no values are undefined if
, and no values are undefined if  or
or 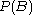 is 0.
is 0.
In general, it cannot be assumed that . This can be an insidious error, even for those who are highly conversant with statistics. The relationship between
. This can be an insidious error, even for those who are highly conversant with statistics. The relationship between  and
and  is given by Bayes' theorem
is given by Bayes' theorem
:
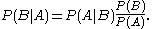
That is,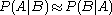 only if
only if 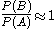 , or equivalently,
, or equivalently,  .
.
In general, it cannot be assumed that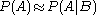 . These probabilities are linked through the formula for total probability:
. These probabilities are linked through the formula for total probability:
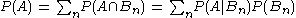 .
.
This fallacy may arise through selection bias
. For example, in the context of a medical claim, let be the event that sequelae
be the event that sequelae 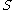 occurs as a consequence of circumstance
occurs as a consequence of circumstance 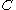 . Let
. Let  be the event that an individual seeks medical help. Suppose that in most cases,
be the event that an individual seeks medical help. Suppose that in most cases, 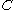 does not cause
does not cause  so
so  is low. Suppose also that medical attention is only sought if
is low. Suppose also that medical attention is only sought if 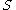 has occurred. From experience of patients, a doctor may therefore erroneously conclude that
has occurred. From experience of patients, a doctor may therefore erroneously conclude that  is high. The actual probability observed by the doctor is
is high. The actual probability observed by the doctor is  .
.
Let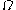 be a sample space with elementary events
be a sample space with elementary events 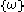 . Suppose we are told the event
. Suppose we are told the event 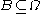 has occurred. A new probability distribution (denoted by the conditional notation) is to be assigned on
has occurred. A new probability distribution (denoted by the conditional notation) is to be assigned on  to reflect this. For events in
to reflect this. For events in  , It is reasonable to assume that the relative magnitudes of the probabilities will be preserved. For some constant scale factor
, It is reasonable to assume that the relative magnitudes of the probabilities will be preserved. For some constant scale factor  , the new distribution will therefore satisfy:
, the new distribution will therefore satisfy:
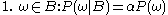
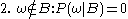

Substituting 1 and 2 into 3 to select :
:


So the new probability distribution is

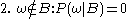
Now for a general event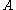 ,
,

 given
given 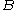 " is the probability of
" is the probability of  if
if 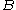 is known to occur. It is commonly notated
is known to occur. It is commonly notated 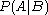 , and sometimes
, and sometimes  . (The vertical line should not be mistaken for logical OR.)
. (The vertical line should not be mistaken for logical OR.)  can be visualised as the probability of event
can be visualised as the probability of event  when the sample space is restricted to event
when the sample space is restricted to event 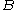 . Mathematically, it is defined for
. Mathematically, it is defined for  as
asFormally,
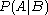 is defined as the probability of
is defined as the probability of 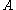 according to a new probability function on the sample space, such that outcomes not in
according to a new probability function on the sample space, such that outcomes not in 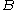 have probability 0 and that it is consistent with all original probability measures
have probability 0 and that it is consistent with all original probability measuresProbability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
. The above definition follows (see Formal derivation).
Conditioning on an event
Given two eventsEvent (probability theory)
In probability theory, an event is a set of outcomes to which a probability is assigned. Typically, when the sample space is finite, any subset of the sample space is an event...
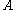 and
and  in the same probability space
in the same probability spaceProbability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
with
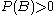 , the conditional probability of
, the conditional probability of 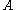 given
given  is defined as the quotient
is defined as the quotientQuotient
In mathematics, a quotient is the result of division. For example, when dividing 6 by 3, the quotient is 2, while 6 is called the dividend, and 3 the divisor. The quotient further is expressed as the number of times the divisor divides into the dividend e.g. The quotient of 6 and 2 is also 3.A...
of the unconditional joint probability of
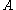 and
and 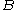 , and the unconditional probability
, and the unconditional probabilityProbability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
of
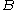 :
:Definition with σ-algebra
If , then the simple definition of
, then the simple definition of  is undefined. However, it is possible to define a conditional probability with respect to a σ-algebra of such events (such as those arising from a continuous random variable).
is undefined. However, it is possible to define a conditional probability with respect to a σ-algebra of such events (such as those arising from a continuous random variable).For example, if X and Y are non-degenerate and jointly continuous random variables with density ƒX,Y(x, y) then, if B has positive measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
,

The case where B has zero measure can only be dealt with directly in the case that B={y0}, representing a single point, in which case

If A has measure zero then the conditional probability is zero. An indication of why the more general case of zero measure cannot be dealt with in a similar way can be seen by noting that the limit, as all δyi approach zero, of

depends on their relationship as they approach zero. See conditional expectation
Conditional expectation
In probability theory, a conditional expectation is the expected value of a real random variable with respect to a conditional probability distribution....
for more information.
Conditioning on a random variable
Conditioning on an event may be generalized to conditioning on a random variable. Let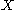 be a random variable taking some value from
be a random variable taking some value from  . Let
. Let  be an event. The probability of
be an event. The probability of 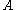 given
given  is defined as
is defined as
Note that
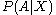 and
and  are now both random variable
are now both random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s. From the law of total probability
Law of total probability
In probability theory, the law of total probability is a fundamental rule relating marginal probabilities to conditional probabilities.-Statement:The law of total probability is the proposition that if \left\...
, the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of
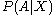 is equal to the unconditional probability
is equal to the unconditional probabilityProbability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
of
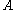 .
.Example
Consider the rolling of two fair six-sided diceDice
A die is a small throwable object with multiple resting positions, used for generating random numbers...
.
- Let
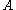 be the value rolled on 1
be the value rolled on 1 - Let
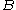 be the value rolled on 2
be the value rolled on 2 - Let
 be the event that
be the event that 
- Let
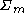 be the event that
be the event that 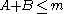
Suppose we roll
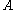 and
and  . What is the probability that
. What is the probability that  ? Table 1 shows the sample space.
? Table 1 shows the sample space. 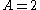 in 6 of the 36 outcomes, so
in 6 of the 36 outcomes, so 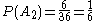 .
.| + | B=1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| A=1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Suppose however that somebody else rolls the dice in secret, revealing only that
 . Table 2 shows that
. Table 2 shows that 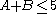 for 10 outcomes.
for 10 outcomes.  in 3 of these. The probability that
in 3 of these. The probability that 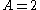 given that
given that  is therefore
is therefore  . This is a conditional probability, because it has a condition that limits the sample space. In more compact notation,
. This is a conditional probability, because it has a condition that limits the sample space. In more compact notation, 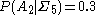 .
.| + | B=1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| A=1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Statistical independence
If two eventsEvent (probability theory)
In probability theory, an event is a set of outcomes to which a probability is assigned. Typically, when the sample space is finite, any subset of the sample space is an event...
 and
and  are statistically independent
are statistically independentStatistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
, the occurrence of
 does not affect the probability of
does not affect the probability of 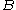 , and vice versa. That is,
, and vice versa. That is,
 .
.Using the definition of conditional probability, it follows from either formula that

This is the definition of statistical independence
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
. This form is the preferred definition, as it is symmetrical in
 and
and  , and no values are undefined if
, and no values are undefined if  or
or 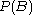 is 0.
is 0.Assuming conditional probability is of similar size to its inverse
In general, it cannot be assumed that
 . This can be an insidious error, even for those who are highly conversant with statistics. The relationship between
. This can be an insidious error, even for those who are highly conversant with statistics. The relationship between  and
and  is given by Bayes' theorem
is given by Bayes' theoremBayes' theorem
In probability theory and applications, Bayes' theorem relates the conditional probabilities P and P. It is commonly used in science and engineering. The theorem is named for Thomas Bayes ....
:
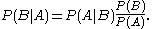
That is,
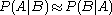 only if
only if 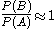 , or equivalently,
, or equivalently,  .
.Assuming marginal and conditional probabilities are of similar size
In general, it cannot be assumed that
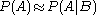 . These probabilities are linked through the formula for total probability:
. These probabilities are linked through the formula for total probability: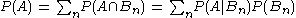 .
.This fallacy may arise through selection bias
Selection bias
Selection bias is a statistical bias in which there is an error in choosing the individuals or groups to take part in a scientific study. It is sometimes referred to as the selection effect. The term "selection bias" most often refers to the distortion of a statistical analysis, resulting from the...
. For example, in the context of a medical claim, let
 be the event that sequelae
be the event that sequelae 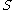 occurs as a consequence of circumstance
occurs as a consequence of circumstance 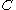 . Let
. Let  be the event that an individual seeks medical help. Suppose that in most cases,
be the event that an individual seeks medical help. Suppose that in most cases, 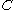 does not cause
does not cause  so
so  is low. Suppose also that medical attention is only sought if
is low. Suppose also that medical attention is only sought if 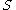 has occurred. From experience of patients, a doctor may therefore erroneously conclude that
has occurred. From experience of patients, a doctor may therefore erroneously conclude that  is high. The actual probability observed by the doctor is
is high. The actual probability observed by the doctor is  .
.Formal derivation
This section is based on the derivation given in Grinsted and Snell's Introduction to Probability.Let
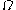 be a sample space with elementary events
be a sample space with elementary events 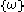 . Suppose we are told the event
. Suppose we are told the event 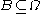 has occurred. A new probability distribution (denoted by the conditional notation) is to be assigned on
has occurred. A new probability distribution (denoted by the conditional notation) is to be assigned on  to reflect this. For events in
to reflect this. For events in  , It is reasonable to assume that the relative magnitudes of the probabilities will be preserved. For some constant scale factor
, It is reasonable to assume that the relative magnitudes of the probabilities will be preserved. For some constant scale factor  , the new distribution will therefore satisfy:
, the new distribution will therefore satisfy: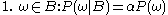
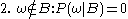

Substituting 1 and 2 into 3 to select
 :
:

So the new probability distribution is

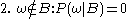
Now for a general event
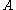 ,
,
See also
- Borel–Kolmogorov paradox
- Chain rule (probability)Chain rule (probability)In probability theory, the chain rule permits the calculation of any member of the joint distribution of a set of random variables using only conditional probabilities.Consider an indexed set of sets A_1, \ldots A_n...
- Posterior probabilityPosterior probabilityIn Bayesian statistics, the posterior probability of a random event or an uncertain proposition is the conditional probability that is assigned after the relevant evidence is taken into account...
- Conditioning (probability)Conditioning (probability)Beliefs depend on the available information. This idea is formalized in probability theory by conditioning. Conditional probabilities, conditional expectations and conditional distributions are treated on three levels: discrete probabilities, probability density functions, and measure theory...
- Joint probability distribution
- Conditional probability distribution
- Class membership probabilitiesClass membership probabilitiesIn general proplems of classification, class membership probabilities reflect the uncertainty with which a given indivual item can be assigned to any given class. Although statistical classification methods by definition generate such probabilities, applications of classification in machine...



