
Skew-Hermitian matrix
Encyclopedia
In linear algebra
, a square matrix with complex
entries is said to be skew-Hermitian or antihermitian if its conjugate transpose
is equal to its negative. That is, the matrix A is skew-Hermitian if it satisfies the relation
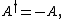
where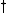 denotes the conjugate transpose of a matrix. In component form, this means that
denotes the conjugate transpose of a matrix. In component form, this means that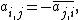
for all i and j, where ai,j is the i,j-th entry of A, and the overline denotes complex conjugation
.
Skew-Hermitian matrices can be understood as the complex versions of real skew-symmetric matrices
, or as the matrix analogue of the purely imaginary numbers. All skew-Hermitian n×n matrices form the u(n) Lie algebra
, which corresponds to the Lie group U(n)
.
The concept can be generalized to include linear transformation
s of any complex
vector space
with a sesquilinear norm
.

Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a square matrix with complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
entries is said to be skew-Hermitian or antihermitian if its conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
is equal to its negative. That is, the matrix A is skew-Hermitian if it satisfies the relation
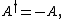
where
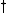 denotes the conjugate transpose of a matrix. In component form, this means that
denotes the conjugate transpose of a matrix. In component form, this means that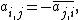
for all i and j, where ai,j is the i,j-th entry of A, and the overline denotes complex conjugation
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
.
Skew-Hermitian matrices can be understood as the complex versions of real skew-symmetric matrices
Skew-symmetric matrix
In mathematics, and in particular linear algebra, a skew-symmetric matrix is a square matrix A whose transpose is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e...
, or as the matrix analogue of the purely imaginary numbers. All skew-Hermitian n×n matrices form the u(n) Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
, which corresponds to the Lie group U(n)
Unitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
.
The concept can be generalized to include linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
s of any complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
with a sesquilinear norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
.
Example
For example, the following matrix is skew-Hermitian:
Properties
- The eigenvalues of a skew-Hermitian matrix are all purely imaginary. Furthermore, skew-Hermitian matrices are normalNormal matrixA complex square matrix A is a normal matrix ifA^*A=AA^* \ where A* is the conjugate transpose of A. That is, a matrix is normal if it commutes with its conjugate transpose.If A is a real matrix, then A*=AT...
. Hence they are diagonalizable and their eigenvectors for distinct eigenvalues must be orthogonal. - All entries on the main diagonal of a skew-Hermitian matrix have to be pure imaginaryImaginary numberAn imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
, i.e., on the imaginary axis (the number zero is also considered purely imaginary). - If A, B are skew-Hermitian, then aA + bB is skew-Hermitian for all realReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
scalarsScalar (mathematics)In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
a and b. - If A is skew-Hermitian, then both iA and -iA are Hermitian.
- If A is skew-Hermitian, then Ak is Hermitian if k is an even integer and skew-Hermitian if k is an odd integer.
- An arbitrary (square) matrix C can uniquely be written as the sum of a Hermitian matrix A and a skew-Hermitian matrix B:
-
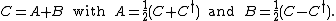
- If A is skew-Hermitian, then eA is unitary.
- The space of skew-Hermitian matrices forms the Lie algebraLie algebraIn mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
u(n) of the Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
U(n).

