
Singular measure
Encyclopedia
In mathematics
, two positive (or signed
or complex
) measures μ and ν defined on a measurable space (Ω, Σ) are called singular if there exist two disjoint sets A and B in Σ whose union is Ω such that μ is zero on all measurable subsets of B while ν is zero on all measurable subsets of A. This is denoted by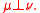
A refined form of Lebesgue's decomposition theorem
decomposes a singular measure into a singular continuous measure and a discrete measure
. See below for examples.
Rn is called singular, if it is singular in respect to the Lebesgue measure
on this space. For example, the Dirac delta function
is a singular measure.
Example. A discrete measure
.
The Heaviside step function
on the real line
,
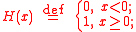
has the Dirac delta distribution
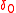 as its distributional derivative. This is a measure on the real line, a "point mass" at 0. However, the Dirac measure
as its distributional derivative. This is a measure on the real line, a "point mass" at 0. However, the Dirac measure 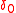 is not absolutely continuous with respect to Lebesgue measure
is not absolutely continuous with respect to Lebesgue measure  , nor is
, nor is  absolutely continuous with respect to
absolutely continuous with respect to  :
: 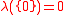 but
but 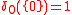 ; if
; if  is any open set
is any open set
not containing 0, then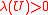 but
but 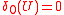 .
.
Example. A singular continuous measure.
The Cantor distribution has a cumulative distribution function
that is continuous but not absolutely continuous, and indeed its absolutely continuous part is zero: it is singular continuous.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, two positive (or signed
Signed measure
In mathematics, signed measure is a generalization of the concept of measure by allowing it to have negative values. Some authors may call it a charge, by analogy with electric charge, which is a familiar distribution that takes on positive and negative values.-Definition:There are two slightly...
or complex
Complex measure
In mathematics, specifically measure theory, a complex measure generalizes the concept of measure by letting it have complex values. In other words, one allows for sets whose size is a complex number.-Definition:...
) measures μ and ν defined on a measurable space (Ω, Σ) are called singular if there exist two disjoint sets A and B in Σ whose union is Ω such that μ is zero on all measurable subsets of B while ν is zero on all measurable subsets of A. This is denoted by
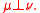
A refined form of Lebesgue's decomposition theorem
Lebesgue's decomposition theorem
In mathematics, more precisely in measure theory, Lebesgue's decomposition theorem is a theorem which states that given \mu and \nu two σ-finite signed measures on a measurable space , there exist two σ-finite signed measures \nu_0 and \nu_1 such that:* \nu=\nu_0+\nu_1\, * \nu_0\ll\mu *...
decomposes a singular measure into a singular continuous measure and a discrete measure
Discrete measure
In mathematics, more precisely in measure theory, a measure on the real line is called a discrete measure if its support is at most a countable set. Note that the support need not be a discrete set...
. See below for examples.
Examples on Rn
As a particular case, a measure defined on the Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn is called singular, if it is singular in respect to the Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
on this space. For example, the Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
is a singular measure.
Example. A discrete measure
Discrete measure
In mathematics, more precisely in measure theory, a measure on the real line is called a discrete measure if its support is at most a countable set. Note that the support need not be a discrete set...
.
The Heaviside step function
Heaviside step function
The Heaviside step function, or the unit step function, usually denoted by H , is a discontinuous function whose value is zero for negative argument and one for positive argument....
on the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
,
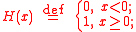
has the Dirac delta distribution
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
 as its distributional derivative. This is a measure on the real line, a "point mass" at 0. However, the Dirac measure
as its distributional derivative. This is a measure on the real line, a "point mass" at 0. However, the Dirac measure  is not absolutely continuous with respect to Lebesgue measure
is not absolutely continuous with respect to Lebesgue measure  , nor is
, nor is  absolutely continuous with respect to
absolutely continuous with respect to  :
: 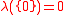 but
but 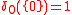 ; if
; if  is any open set
is any open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
not containing 0, then
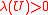 but
but 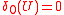 .
.Example. A singular continuous measure.
The Cantor distribution has a cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
that is continuous but not absolutely continuous, and indeed its absolutely continuous part is zero: it is singular continuous.
See also
- Lebesgue's decomposition theoremLebesgue's decomposition theoremIn mathematics, more precisely in measure theory, Lebesgue's decomposition theorem is a theorem which states that given \mu and \nu two σ-finite signed measures on a measurable space , there exist two σ-finite signed measures \nu_0 and \nu_1 such that:* \nu=\nu_0+\nu_1\, * \nu_0\ll\mu *...
- Absolutely continuous
- Singular distributionSingular distributionIn probability, a singular distribution is a probability distribution concentrated on a set of Lebesgue measure zero, where the probability of each point in that set is zero. These distributions are sometimes called singular continuous distributions...

