
Schild's ladder
Encyclopedia
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, and differential geometry more generally, Schild's ladder is a first-order method for approximating parallel transport
Parallel transport
In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...
of a vector along a curve using only affinely parametrized geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s. The method is named for Alfred Schild
Alfred Schild
Alfred Schild was a leading American physicist, well-known for his contributions to the Golden age of general relativity ....
, who introduced the method during lectures at Princeton University
Princeton University
Princeton University is a private research university located in Princeton, New Jersey, United States. The school is one of the eight universities of the Ivy League, and is one of the nine Colonial Colleges founded before the American Revolution....
.
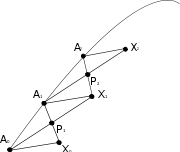
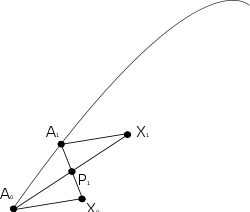
Construction
The idea is to identify a tangent vector x at a point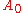 with a geodesic segment of unit length
with a geodesic segment of unit length  , and to construct an approximate parallelogram with approximately parallel sides
, and to construct an approximate parallelogram with approximately parallel sides 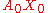 and
and 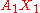 as an approximation of the Levi-Civita parallelogramoid
as an approximation of the Levi-Civita parallelogramoidLevi-Civita parallelogramoid
In the mathematical field of differential geometry, the Levi-Civita parallelogramoid is a certain figure generalizing a parallelogram to a curved space. It is named for its discoverer, Tullio Levi-Civita...
; the new segment
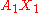 thus corresponds to an approximately parallel translated tangent vector at
thus corresponds to an approximately parallel translated tangent vector at 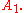
 |
 |
 |
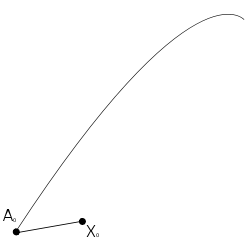
Formally, consider a curve γ through a point A0 in a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
M, and let x be a tangent vector
Tangent vector
A tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....
at A0. Then x can be identified with a geodesic segment A0X0 via the exponential map
Exponential map
In differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....
. This geodesic σ satisfies
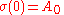
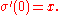
The steps of the Schild's ladder construction are:
- Let X0 = σ(1), so the geodesic segment
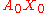 has unit length.
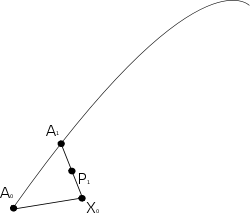
has unit length. - Now let A1 be a point on γ close to A0, and construct the geodesic X0A1.
- Let P1 be the midpoint of X0A1 in the sense that the segments X0P1 and P1A1 take an equal affine parameter to traverse.
- Construct the geodesic A0P1, and extend it to a point X1 so that the parameter length of A0X1 is double that of A0P1.
- Finally construct the geodesic A1X1. The tangent to this geodesic x1 is then the parallel transport of X0 to A1, at least to first order.
Approximation
This is a discrete approximation of the continuous process of parallel transport. If the ambient space is flat, this is exactly parallel transport, and the steps define parallelograms, which agree with the Levi-Civita parallelogramoidLevi-Civita parallelogramoid
In the mathematical field of differential geometry, the Levi-Civita parallelogramoid is a certain figure generalizing a parallelogram to a curved space. It is named for its discoverer, Tullio Levi-Civita...
.
In a curved space, the error is given by holonomy
Holonomy
In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...
around the triangle
 which is equal to the integral of the curvature
which is equal to the integral of the curvatureCurvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
over the interior of the triangle, by the Ambrose-Singer theorem; this is a form of Green's theorem
Green's theorem
In mathematics, Green's theorem gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C...
(integral around a curve related to integral over interior).

