Regular category
Encyclopedia
In category theory
, a regular category is a category with finite limits
and coequalizer
s of kernel pairs, satisfying certain exactness conditions. In that way, regular categories recapture many properties of abelian categories, like the existence of images, without requiring additivity. At the same time, regular categories provide a foundation for the study of a fragment of first-order logic
, known as regular logic.
The following categories are not regular:
s and the monomorphism
s form a factorization system
. Every morphism f:X→Y can be factorized into a regular epimorphism
e:X→E followed by a monomorphism
m:E→Y, so that f=me. The factorization is unique in the sense that if e':X→E' is another regular epimorphism and m':E'→Y is another monomorphism such that f=m'e, then there exists an isomorphism h:E→E' such that he=e' and m'h=m. The monomorphism m is called the image of f.
is said to be an exact sequence if it is both a coequalizer and a kernel pair. The terminology is a generalization of exact sequences in homological algebra
: in an abelian category
, a diagram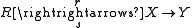
is exact in this sense if and only if
is a short exact sequence in the usual sense.
A functor between regular categories is called regular, if it preserves finite limits and coequalizers of kernel pairs. A functor is regular if and only if it preserves finite limits and exact sequences. For this reason, regular functors are sometimes called exact functors. Functors that preserve finite limits are often said to be left exact.
that can express statements of the form
,
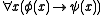where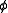
and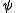 
are regular formulae i.e. formulae built up from atomic formula
e, the truth constant, binary meets
and existential quantification
. Such formulae can be interpreted in a regular category, and the interpretation is a model of a sequent
,
if the interpretation of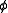
factors through the interpretation of 
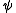. This gives for each theory (set of sequences) and for each regular category C a category Mod(T,C) of models of T in C. This construction gives a functor Mod(T,-):RegCat→Cat from the category RegCat of small regular categories and regular functors to small categories. It is an important result that for each theory T and for each category C, there is a category R(T) and an equivalence
,
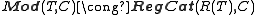which is natural in C. Up to equivalence any small regular category C arises this way as the classifying category, of a regular theory.
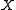of a regular category is a monomorphism into 
that satisfies the interpretations of the conditions for reflexivity, symmetry and transitivity.
Every kernel pair
defines an equivalence relation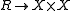 
. Conversely, an equivalence relation is said to be effective if it arises as a kernel pair. An equivalence relation is effective if and only if it has a coequalizer and it is the kernel pair of this.
A regular category is said to be exact, or exact in the sense of Barr
, or effective regular, if every equivalence relation is effective.
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a regular category is a category with finite limits
Limit (category theory)
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
and coequalizer
Coequalizer
In category theory, a coequalizer is a generalization of a quotient by an equivalence relation to objects in an arbitrary category...
s of kernel pairs, satisfying certain exactness conditions. In that way, regular categories recapture many properties of abelian categories, like the existence of images, without requiring additivity. At the same time, regular categories provide a foundation for the study of a fragment of first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
, known as regular logic.
Definition
A category C is called regular if it satisfies the following three properties:- C is finitely complete.
- If f:X→Y is a morphismMorphismIn mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
in C, and
- is a pullbackPullback (category theory)In category theory, a branch of mathematics, a pullback is the limit of a diagram consisting of two morphisms f : X → Z and g : Y → Z with a common codomain; it is the limit of the cospan X \rightarrow Z \leftarrow Y...
, then the coequalizer of p0,p1 exists. The pair (p0,p1) is called the kernel pair of f. Being a pullback, the kernel pair is unique up to a unique isomorphismIsomorphismIn abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
.- If f:X→Y is a morphism in C, and
- is a pullback, and if f is a regular epimorphismEpimorphismIn category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
, then g is a regular epimorphism as well. A regular epimorphism is an epimorphism which appears as a coequalizer of some pair of morphisms.
Examples
Examples of regular categories include:- SetCategory of setsIn the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
, the category of sets and functionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s between the sets - More generally, every elementary toposToposIn mathematics, a topos is a type of category that behaves like the category of sheaves of sets on a topological space...
- Grp, the category of groupsGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
and group homomorphismGroup homomorphismIn mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
s - The category of fieldsField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
and ring homomorphismRing homomorphismIn ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
s - Every bounded join-semilatticeSemilatticeIn mathematics, a join-semilattice is a partially ordered set which has a join for any nonempty finite subset. Dually, a meet-semilattice is a partially ordered set which has a meet for any nonempty finite subset...
, with morphisms given by the order relation - Abelian categories
The following categories are not regular:
- Top, the category of topological spaceTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s and continuous functions - Cat, the category of small categories and functorFunctorIn category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
s
Epi-mono factorization
In a regular category, the regular-epimorphismEpimorphism
In category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
s and the monomorphism
Monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
s form a factorization system
Factorization system
In mathematics, it can be shown that every function can be written as the composite of a surjective function followed by an injective function. Factorization systems are a generalization of this situation in category theory.-Definition:...
. Every morphism f:X→Y can be factorized into a regular epimorphism
Epimorphism
In category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
e:X→E followed by a monomorphism
Monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
m:E→Y, so that f=me. The factorization is unique in the sense that if e':X→E' is another regular epimorphism and m':E'→Y is another monomorphism such that f=m'e, then there exists an isomorphism h:E→E' such that he=e' and m'h=m. The monomorphism m is called the image of f.
Exact sequences and regular functors
In a regular category, a diagram of the form is said to be an exact sequence if it is both a coequalizer and a kernel pair. The terminology is a generalization of exact sequences in homological algebraHomological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
: in an abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
, a diagram
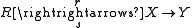
is exact in this sense if and only if
is a short exact sequence in the usual sense.A functor between regular categories is called regular, if it preserves finite limits and coequalizers of kernel pairs. A functor is regular if and only if it preserves finite limits and exact sequences. For this reason, regular functors are sometimes called exact functors. Functors that preserve finite limits are often said to be left exact.
Regular logic and regular categories
Regular logic is the fragment of first-order logicFirst-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
that can express statements of the form
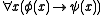,where
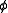and 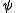are regular formulae i.e. formulae built up from atomic formulaAtomic formula
In mathematical logic, an atomic formula is a formula with no deeper propositional structure, that is, a formula that contains no logical connectives or equivalently a formula that has no strict subformulas. Atoms are thus the simplest well-formed formulas of the logic...
e, the truth constant, binary meets
Meet (mathematics)
In mathematics, join and meet are dual binary operations on the elements of a partially ordered set. A join on a set is defined as the supremum with respect to a partial order on the set, provided a supremum exists...
and existential quantification
Existential quantification
In predicate logic, an existential quantification is the predication of a property or relation to at least one member of the domain. It is denoted by the logical operator symbol ∃ , which is called the existential quantifier...
. Such formulae can be interpreted in a regular category, and the interpretation is a model of a sequent
Sequent
In proof theory, a sequent is a formalized statement of provability that is frequently used when specifying calculi for deduction. In the sequent calculus, the name sequent is used for the construct which can be regarded as a specific kind of judgment, characteristic to this deduction system.-...
,if the interpretation of
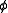factors through the interpretation of 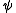. This gives for each theory (set of sequences) and for each regular category C a category Mod(T,C) of models of T in C. This construction gives a functor Mod(T,-):RegCat→Cat from the category RegCat of small regular categories and regular functors to small categories. It is an important result that for each theory T and for each category C, there is a category R(T) and an equivalence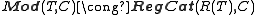,which is natural in C. Up to equivalence any small regular category C arises this way as the classifying category, of a regular theory.
Exact (effective) categories
The theory of equivalence relations is a regular theory. An equivalence relation on an object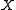 of a regular category is a monomorphism into that satisfies the interpretations of the conditions for reflexivity, symmetry and transitivity.Every kernel pair
defines an equivalence relation 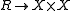. Conversely, an equivalence relation is said to be effective if it arises as a kernel pair. An equivalence relation is effective if and only if it has a coequalizer and it is the kernel pair of this.A regular category is said to be exact, or exact in the sense of Barr
Michael Barr (mathematician)
Michael Barr is Peter Redpath Emeritus Professor of Pure Mathematics at McGill University. Although his earlier work was in homological algebra, his principal research area for a number of years has been category theory...
, or effective regular, if every equivalence relation is effective.
Examples of exact categories
- The category of setsCategory of setsIn the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
is exact in this sense, and so is any (elementary) toposToposIn mathematics, a topos is a type of category that behaves like the category of sheaves of sets on a topological space...
. Every equivalence relation has a coequalizer, which is found by taking equivalence classes. - Every abelian categoryAbelian categoryIn mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
is exact. - Every category that is monadicMonad (category theory)In category theory, a branch of mathematics, a monad, Kleisli triple, or triple is an functor, together with two natural transformations...
over the category of sets is exact. - The category of Stone spaces is exact.