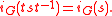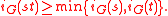Ramification group
Encyclopedia
In number theory
, more specifically in local class field theory, the ramification groups are a filtration of the Galois group
of a local field
extension, which gives a precisely information on the ramification
phenomenon of the extension.
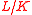be a finite Galois extension of local fields with group 
and finite residue fields 
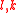. We shall write 
for the valuation, the ring of integers and its maximal ideal for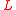 
. It is known that one can write 
for som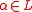e 
where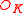 
is the ring of integers of 
. (This is stronger than the primitive element theorem and is a consequence of Hensel's lemma.) Then, for each integer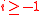 
, we define 
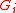to be the set of all 
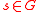that satisfies the following equivalent conditions.
(i) shows that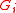
are normal and (ii) shows that 
for sufficiently large 
. 
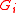is then called the 
-th ramification group, and they form a finite decreasing filtration of 
with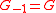 
. 
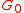is called the inertia subgroup of 
. Note:
The study of ramification groups reduces to the totally ramified case since one has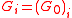
for 
.
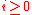One also defines the function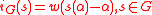
. (ii) in the above shows 
is independent of choice of 
and, moreover, the study of the filtration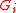 
is essentially equivalent to that of 
. 
satisfies the following: for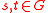 
,
Fix a uniformizer
of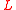 
. 
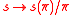then induces the injection 
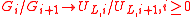where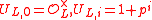 
. It follows from this
In particular,
is a p-group
and
is solvable
.
The ramification groups can be used to compute the different
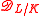of the extension 
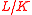and that of subextensions: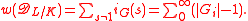
If
is a normal subgroup of 
, then, for 
, 
.
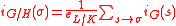Combing this with the above one obtains: for a subextension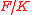
corresponding to 
,
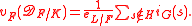
If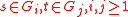
, then 
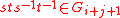. In the terminology of Lazard, this can be understood to mean the Lie algebra
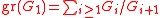is abelian.
is a real number 
, let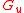 
denote 
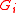where i the least integer 
. In other words, 
Define 
by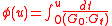
where, by convention,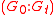
is equal to 
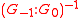if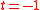 
and is equal to 
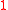for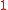 
. Then 
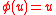for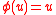 
. It is immediate that 
is continuous and strictly increasing, and thus has the continuous inverse function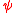 
defined on 
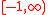. Define
.
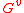is then called the v-th ramification group in upper numbering. In other words, 
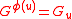. Note 
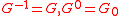. The upper numbering is defined so as to be compatible with passage to quotients: if 
is normal in 
, then
for all 
(whereas lower numbering is compatible with passage to subgroups.)
Herbrand's theorem states that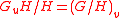
for 
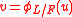where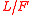 
is a subextension corresponding to 
.
The upper numbering for an abelian extension is important because of the Hasse–Arf theorem
. It states that if
is abelian, then the jumps in the filtration 
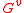are integers; i.e., 
whenever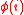 
is not an integer.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, more specifically in local class field theory, the ramification groups are a filtration of the Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
of a local field
Local field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
extension, which gives a precisely information on the ramification
Ramification
In mathematics, ramification is a geometric term used for 'branching out', in the way that the square root function, for complex numbers, can be seen to have two branches differing in sign...
phenomenon of the extension.
Ramification groups in lower numbering
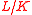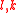Let be a finite Galois extension of local fields with group and finite residue fields . We shall write for the valuation, the ring of integers and its maximal ideal for 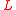. It is known that one can write for som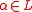e where 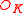is the ring of integers of . (This is stronger than the primitive element theorem and is a consequence of Hensel's lemma.) Then, for each integer 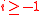, we define 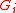to be the set of all 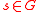that satisfies the following equivalent conditions.
- (i)
operates trivially on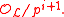 
- (ii)
for all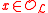 
- (iii)
(i) shows that
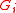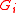are normal and (ii) shows that for sufficiently large . is then called the -th ramification group, and they form a finite decreasing filtration of with 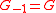. 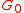is called the inertia subgroup of . Note:
unramified.
tamely ramified (i.e., the ramification index is prime to the residue characteristic.)
The study of ramification groups reduces to the totally ramified case since one has
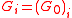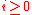for .One also defines the function
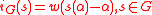. (ii) in the above shows is independent of choice of and, moreover, the study of the filtration 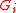is essentially equivalent to that of . satisfies the following: for ,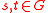
Fix a uniformizer
of 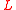. 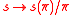then induces the injection 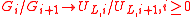where 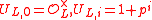. It follows from this
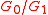is cyclic of order prime to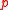 
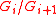is a product of cyclic groups of order 
.
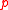In particular,
is a p-groupP-group
In mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...
and
is solvableSolvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
.
The ramification groups can be used to compute the different
Different ideal
In algebraic number theory, the different ideal is defined to account for the lack of duality in the ring of integers of an algebraic number field K, with respect to the field trace...
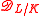of the extension 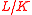and that of subextensions: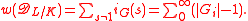If
is a normal subgroup of , then, for , 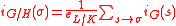.Combing this with the above one obtains: for a subextension
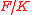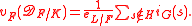
corresponding to ,If
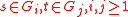, then 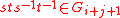. In the terminology of Lazard, this can be understood to mean the Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
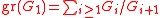is abelian.Ramification groups in upper numbering
If is a real number , let 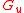denote 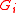where i the least integer . In other words, Define by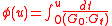where, by convention,
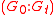is equal to 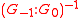if 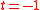and is equal to 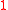for 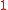. Then 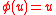for 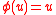. It is immediate that is continuous and strictly increasing, and thus has the continuous inverse function 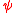defined on 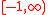. Define. 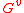is then called the v-th ramification group in upper numbering. In other words, 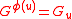. Note 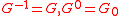. The upper numbering is defined so as to be compatible with passage to quotients: if is normal in , then for all (whereas lower numbering is compatible with passage to subgroups.)
Herbrand's theorem states that
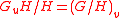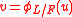for where 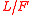is a subextension corresponding to .The upper numbering for an abelian extension is important because of the Hasse–Arf theorem
Hasse–Arf theorem
In mathematics, specifically in local class field theory, the Hasse–Arf theorem is a result concerning jumps of a filtration of the Galois group of a finite Galois extension...
. It states that if
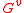is abelian, then the jumps in the filtration are integers; i.e., whenever 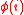is not an integer.