Quantum calculus
Encyclopedia
Quantum calculus is equivalent to traditional infinitesimal calculus
without the notion of limits
. It defines "q-calculus" and "h-calculus". h ostensibly stands for Planck's constant while q stands for quantum. The two parameters are related by the formula
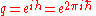
where
is the reduced Planck constant.
of functions are defined as
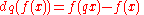
and
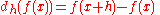
respectively. Derivative
s of functions are then defined as fractions by the q-derivative
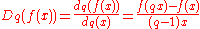
and by
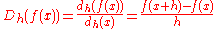
In the limit
, as h goes to 0, or equivalently as q goes to 1, these expressions take on the form of the derivative of classical calculus.
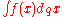and an expression for F(x) can be found from the formula
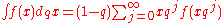which is called the Jackson integral
of f(x). For 0 < q < 1, the series converges to a function F(x) on an interval (0,A] if |f(x)x^α| is bounded on the interval (0,A] for some 0 <= α < 1.
The q-integral is a Riemann-Stieltjes integral
with respect to a step function
having infinitely many points of increase at the points qj, with the jump at the point qj being qj. If we call this step function gq(t) then dgq(t) = dqt.
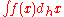. If a and b differ by an integer multiple of h then the definite integral
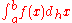is given by a Riemann sum
of f(x) on the interval [a,b] partitioned into subintervals of width h.
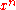(for some positive integer 
) in the classical calculus is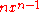 
. The corresponding expressions in q-calculus and h-calculus are
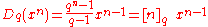
with the q-bracket
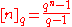
and
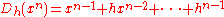
respectively. The expression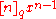
is then the q-calculus analogue of the simple power rule for
positive integral powers. In this sense, the function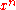
is still nice in the q-calculus, but rather
ugly in the h-calculus – the h-calculus analog of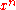
is instead the falling factorial,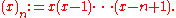 
One may proceed further and develop, for example, equivalent notions of Taylor expansion
, et cetera, and even arrive at q-calculus analogues for all of the usual functions one would want to have, such as an analogue for the sine
function whose q-derivative is the appropriate analogue for the cosine.
and others, and has proven useful in a number of fields, among them combinatorics
and fluid mechanics
. The q-calculus, while dating in a sense back to Leonhard Euler
and Carl Gustav Jacobi, is only recently beginning to see more usefulness in quantum mechanics
, having an intimate connection with commutativity relations and Lie algebra
.
Infinitesimal calculus
Infinitesimal calculus is the part of mathematics concerned with finding slope of curves, areas under curves, minima and maxima, and other geometric and analytic problems. It was independently developed by Gottfried Leibniz and Isaac Newton starting in the 1660s...
without the notion of limits
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
. It defines "q-calculus" and "h-calculus". h ostensibly stands for Planck's constant while q stands for quantum. The two parameters are related by the formula
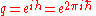
where
is the reduced Planck constant.Differentiation
In the q-calculus and h-calculus, differentialsDifferential of a function
In calculus, the differential represents the principal part of the change in a function y = ƒ with respect to changes in the independent variable. The differential dy is defined bydy = f'\,dx,...
of functions are defined as
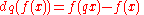
and
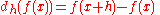
respectively. Derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s of functions are then defined as fractions by the q-derivative
Q-derivative
In mathematics, in the area of combinatorics, the q-derivative, or Jackson derivative, is a q-analog of the ordinary derivative, introduced by Frank Hilton Jackson. It is the inverse of Jackson's q-integration-Definition:...
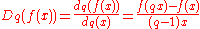
and by
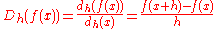
In the limit
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
, as h goes to 0, or equivalently as q goes to 1, these expressions take on the form of the derivative of classical calculus.
q-integral
A function F(x) is a q-antiderivative of f(x) if DqF(x)=f(x). The q-antiderivative (or q-integral) is denoted by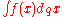 and an expression for F(x) can be found from the formula 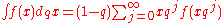which is called the Jackson integralJackson integral
In q-analog theory, the Jackson integral series in the theory of special functions that expresses the operation inverse to q-differentiation.The Jackson integral was introduced by Frank Hilton Jackson.- Definition :...
of f(x). For 0 < q < 1, the series converges to a function F(x) on an interval (0,A] if |f(x)x^α| is bounded on the interval (0,A] for some 0 <= α < 1.
The q-integral is a Riemann-Stieltjes integral
Riemann-Stieltjes integral
In mathematics, the Riemann–Stieltjes integral is a generalization of the Riemann integral, named after Bernhard Riemann and Thomas Joannes Stieltjes.-Definition:...
with respect to a step function
Step function
In mathematics, a function on the real numbers is called a step function if it can be written as a finite linear combination of indicator functions of intervals...
having infinitely many points of increase at the points qj, with the jump at the point qj being qj. If we call this step function gq(t) then dgq(t) = dqt.
h-integral
A function F(x) is an h-antiderivative of f(x) if DhF(x)=f(x). The h-antiderivative (or h-integral) is denoted by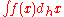. If a and b differ by an integer multiple of h then the definite integral 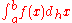is given by a Riemann sumRiemann sum
In mathematics, a Riemann sum is a method for approximating the total area underneath a curve on a graph, otherwise known as an integral. It mayalso be used to define the integration operation. The method was named after German mathematician Bernhard Riemann....
of f(x) on the interval [a,b] partitioned into subintervals of width h.
Example
The derivative of the function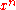 (for some positive integer ) in the classical calculus is 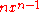. The corresponding expressions in q-calculus and h-calculus are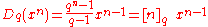with the q-bracket
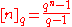
and
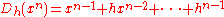
respectively. The expression
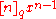is then the q-calculus analogue of the simple power rule forpositive integral powers. In this sense, the function
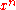is still nice in the q-calculus, but ratherugly in the h-calculus – the h-calculus analog of
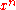is instead the falling factorial,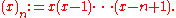 One may proceed further and develop, for example, equivalent notions of Taylor expansion
Q-derivative
In mathematics, in the area of combinatorics, the q-derivative, or Jackson derivative, is a q-analog of the ordinary derivative, introduced by Frank Hilton Jackson. It is the inverse of Jackson's q-integration-Definition:...
, et cetera, and even arrive at q-calculus analogues for all of the usual functions one would want to have, such as an analogue for the sine
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
function whose q-derivative is the appropriate analogue for the cosine.
History
The h-calculus is just the calculus of finite differences, which had been studied by George BooleGeorge Boole
George Boole was an English mathematician and philosopher.As the inventor of Boolean logic—the basis of modern digital computer logic—Boole is regarded in hindsight as a founder of the field of computer science. Boole said,...
and others, and has proven useful in a number of fields, among them combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
and fluid mechanics
Fluid mechanics
Fluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...
. The q-calculus, while dating in a sense back to Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
and Carl Gustav Jacobi, is only recently beginning to see more usefulness in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, having an intimate connection with commutativity relations and Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
.
See also
- Noncommutative geometryNoncommutative geometryNoncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
- Quantum differential calculusQuantum differential calculusIn quantum geometry or noncommutative geometry a quantum differential calculus or noncommtuative differential structure on an algebra A over a field k means the specification of a space of `differential forms' over the algebra...
- Time scale calculusTime scale calculusIn mathematics, time-scale calculus is a unification of the theory of difference equations with that of differential equations, unifying integral and differential calculus with the calculus of finite differences, offering a formalism for studying hybrid discrete–continuous dynamical systems...
- q-analogQ-analogRoughly speaking, in mathematics, specifically in the areas of combinatorics and special functions, a q-analog of a theorem, identity or expression is a generalization involving a new parameter q that returns the original theorem, identity or expression in the limit as q → 1...