
Quantile regression
Encyclopedia
Quantile regression is a type of regression analysis
used in statistics. Whereas the method of least squares results in estimates that approximate the conditional mean of the response variable given certain values of the predictor variables, quantile regression results in estimates approximating either the median
or other quantiles of the response variable.
and statistical dispersion
to obtain a more comprehensive and robust analysis. Another advantage to quantile regression is the fact that any quantile can be estimated.
In ecology
, quantile regression has been proposed and used as a way to discover more useful predictive relationships between variables in cases where there is no relationship or only a weak relationship between the means of such variables. The need for and success of quantile regression in ecology has been attributed to the complexity
of interactions between different factors leading to data
with unequal variation of one variable for different ranges of another variable.
, involving projection
onto subspaces, and thus the problem of minimizing the squared errors can be reduced to a problem in numerical linear algebra
. Quantile regression does not have this structure, and instead leads to problems in linear programming
that can be solved by the simplex method. The fact that the algorithms of linear programming appear more esoteric to users may explain why quantile regression is not as widely used as the method of least squares.
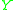 be a real valued random variable with distribution function
be a real valued random variable with distribution function 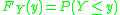 . The
. The  th quantile of Y is given by
th quantile of Y is given by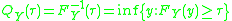
where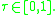
Define the loss function
as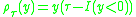 . A specific quantile can be found by minimizing the expected loss of
. A specific quantile can be found by minimizing the expected loss of  with respect to
with respect to  :
: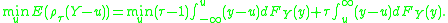
This can be shown by setting the derivative of the expected loss function to 0 and letting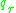 be the solution of
be the solution of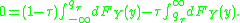
This equation reduces to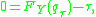
and then to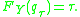
Hence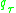 is
is  th quantile of the random variable Y.
th quantile of the random variable Y.
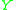 be a discrete random variable that takes values 1,2,..,9 with equal probabilities. The task is to find the median of Y, and hence the value
be a discrete random variable that takes values 1,2,..,9 with equal probabilities. The task is to find the median of Y, and hence the value 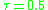 is chosen. The expected loss, , is
is chosen. The expected loss, , is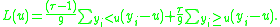
Since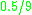 is a constant, it can be taken out of the expected loss function (this is only true if
is a constant, it can be taken out of the expected loss function (this is only true if 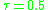 ). Then, at u=3,
). Then, at u=3,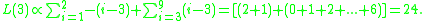
Suppose that u is increased by 1 unit. Then the expected loss will be changed by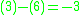 on changing u to 4. If , u=5, the expected loss is
on changing u to 4. If , u=5, the expected loss is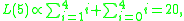
and any change in u will increase the expected loss. Thus u=5 is the median. The Table below shows the expected loss (divided by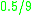 ) for different values of u.
) for different values of u.
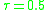 and let q be an initial guess for
and let q be an initial guess for 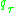 . The expected loss evaluated at q is
. The expected loss evaluated at q is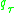
In order to miminize the expected loss, we move the value of q a little bit to see whether the expect loss will rise or fall.
Suppose we increase q by 1 unit. Then the change of expected loss would be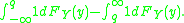
The first term of the equation is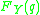 and second term of the equation is
and second term of the equation is 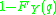 . Therefore the change of expected loss function is negative if and only if
. Therefore the change of expected loss function is negative if and only if 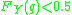 , that is if and only if q is smaller than the median. Similarly, if we reduce q by 1 unit, the change of expected loss function is negative if and only if q is larger than the median.
, that is if and only if q is smaller than the median. Similarly, if we reduce q by 1 unit, the change of expected loss function is negative if and only if q is larger than the median.
In order to minimize the expected loss function, we would increase (decrease) L(q) if q is smaller (larger) than the median, until q reaches the median. The idea behind the minimization is to count the number of points (weighted with the density) that are larger or smaller than q and then move q to a point where q is larger than % of the points.
% of the points.
 sample quantile can be obtained by solving the following minimization problem
sample quantile can be obtained by solving the following minimization problem
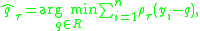
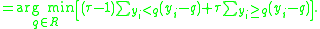
The intuition is the same as for the population quantile.
 th conditional quantile function is
th conditional quantile function is 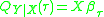 . Given the distribution function of
. Given the distribution function of 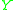 ,
, 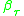 can be obtained by solving
can be obtained by solving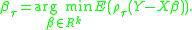
Solving the sample analog gives the estimator of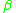 .
.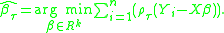
problem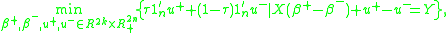
where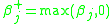 ,
,  ,
, 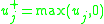 ,
, 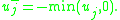
Simplex methods
or interior point method
s can be applied to solve the linear programming problem.
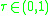 , under some regularity conditions,
, under some regularity conditions, 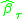 is asymptotically normal:
is asymptotically normal: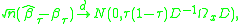
where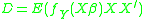 and
and 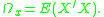
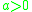 and
and 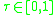
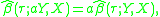
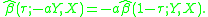
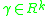 and
and 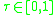
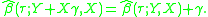
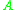 be any
be any 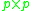 nonsingular matrix and
nonsingular matrix and 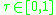
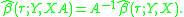
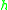 is a nondecreasing function on R, the following invariance
is a nondecreasing function on R, the following invariance
property applies:
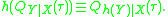
Example 1
Let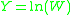 and
and 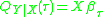 , then
, then 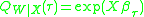 . The mean regression does not have the same property since
. The mean regression does not have the same property since 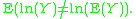
Example 2
Let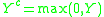 and
and 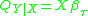 , then
, then 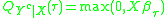 . This is the censored quantile regression model: estimated values can be obtained without making any distributional assumptions, but at the cost of computational difficulty, some of which can be avoided by using a simple three step censored quantile regression procedure as an approximation.
. This is the censored quantile regression model: estimated values can be obtained without making any distributional assumptions, but at the cost of computational difficulty, some of which can be avoided by using a simple three step censored quantile regression procedure as an approximation.
, Eviews
(ver. 6), Stata
(via qreg), gretl
, SAS
through proc quantreg (ver. 9.2), and RATS include implementations of quantile regression. R implements it through Roger Koenker's quantreg package.
Regression analysis
In statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...
used in statistics. Whereas the method of least squares results in estimates that approximate the conditional mean of the response variable given certain values of the predictor variables, quantile regression results in estimates approximating either the median
Median
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
or other quantiles of the response variable.
Advantages and applications
Quantile regression is used when an estimate of the various quantiles (such as the median) of a population is desired. One advantage of using quantile regression to estimate the median, rather than ordinary least squares regression to estimate the mean, is that quantile regression will be more robust in response to large outliers. Quantile regression can be seen as a natural analogue in regression analysis to the practice of using different measures of central tendencyCentral tendency
In statistics, the term central tendency relates to the way in which quantitative data is clustered around some value. A measure of central tendency is a way of specifying - central value...
and statistical dispersion
Statistical dispersion
In statistics, statistical dispersion is variability or spread in a variable or a probability distribution...
to obtain a more comprehensive and robust analysis. Another advantage to quantile regression is the fact that any quantile can be estimated.
In ecology
Ecology
Ecology is the scientific study of the relations that living organisms have with respect to each other and their natural environment. Variables of interest to ecologists include the composition, distribution, amount , number, and changing states of organisms within and among ecosystems...
, quantile regression has been proposed and used as a way to discover more useful predictive relationships between variables in cases where there is no relationship or only a weak relationship between the means of such variables. The need for and success of quantile regression in ecology has been attributed to the complexity
Complexity
In general usage, complexity tends to be used to characterize something with many parts in intricate arrangement. The study of these complex linkages is the main goal of complex systems theory. In science there are at this time a number of approaches to characterizing complexity, many of which are...
of interactions between different factors leading to data
Data
The term data refers to qualitative or quantitative attributes of a variable or set of variables. Data are typically the results of measurements and can be the basis of graphs, images, or observations of a set of variables. Data are often viewed as the lowest level of abstraction from which...
with unequal variation of one variable for different ranges of another variable.
Mathematics
The mathematical forms arising from quantile regression are distinct from those arising in the method of least squares. The method of least squares leads to a consideration of problems in an inner product spaceInner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
, involving projection
Projection (mathematics)
Generally speaking, in mathematics, a projection is a mapping of a set which is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows...
onto subspaces, and thus the problem of minimizing the squared errors can be reduced to a problem in numerical linear algebra
Numerical linear algebra
Numerical linear algebra is the study of algorithms for performing linear algebra computations, most notably matrix operations, on computers. It is often a fundamental part of engineering and computational science problems, such as image and signal processing, Telecommunication, computational...
. Quantile regression does not have this structure, and instead leads to problems in linear programming
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
that can be solved by the simplex method. The fact that the algorithms of linear programming appear more esoteric to users may explain why quantile regression is not as widely used as the method of least squares.
Quantiles
Let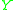 be a real valued random variable with distribution function
be a real valued random variable with distribution function 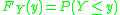 . The
. The  th quantile of Y is given by
th quantile of Y is given by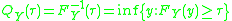
where
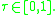
Define the loss function
Loss function
In statistics and decision theory a loss function is a function that maps an event onto a real number intuitively representing some "cost" associated with the event. Typically it is used for parameter estimation, and the event in question is some function of the difference between estimated and...
as
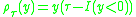 . A specific quantile can be found by minimizing the expected loss of
. A specific quantile can be found by minimizing the expected loss of  with respect to
with respect to  :
: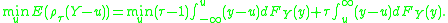
This can be shown by setting the derivative of the expected loss function to 0 and letting
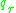 be the solution of
be the solution of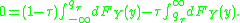
This equation reduces to
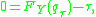
and then to
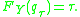
Hence
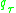 is
is  th quantile of the random variable Y.
th quantile of the random variable Y.Example
Let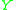 be a discrete random variable that takes values 1,2,..,9 with equal probabilities. The task is to find the median of Y, and hence the value
be a discrete random variable that takes values 1,2,..,9 with equal probabilities. The task is to find the median of Y, and hence the value 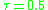 is chosen. The expected loss, , is
is chosen. The expected loss, , is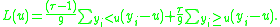
Since
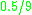 is a constant, it can be taken out of the expected loss function (this is only true if
is a constant, it can be taken out of the expected loss function (this is only true if 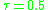 ). Then, at u=3,
). Then, at u=3,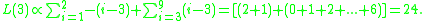
Suppose that u is increased by 1 unit. Then the expected loss will be changed by
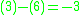 on changing u to 4. If , u=5, the expected loss is
on changing u to 4. If , u=5, the expected loss is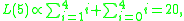
and any change in u will increase the expected loss. Thus u=5 is the median. The Table below shows the expected loss (divided by
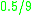 ) for different values of u.
) for different values of u.| u | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| Expected loss | 36 | 29 | 24 | 21 | 20 | 21 | 24 | 29 | 36 |
Intuition
Consider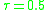 and let q be an initial guess for
and let q be an initial guess for 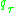 . The expected loss evaluated at q is
. The expected loss evaluated at q is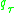
In order to miminize the expected loss, we move the value of q a little bit to see whether the expect loss will rise or fall.
Suppose we increase q by 1 unit. Then the change of expected loss would be
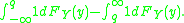
The first term of the equation is
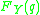 and second term of the equation is
and second term of the equation is 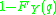 . Therefore the change of expected loss function is negative if and only if
. Therefore the change of expected loss function is negative if and only if 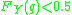 , that is if and only if q is smaller than the median. Similarly, if we reduce q by 1 unit, the change of expected loss function is negative if and only if q is larger than the median.
, that is if and only if q is smaller than the median. Similarly, if we reduce q by 1 unit, the change of expected loss function is negative if and only if q is larger than the median.In order to minimize the expected loss function, we would increase (decrease) L(q) if q is smaller (larger) than the median, until q reaches the median. The idea behind the minimization is to count the number of points (weighted with the density) that are larger or smaller than q and then move q to a point where q is larger than
 % of the points.
% of the points.Sample quantile
The sample quantile can be obtained by solving the following minimization problem
sample quantile can be obtained by solving the following minimization problem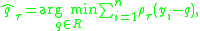
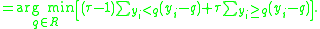
The intuition is the same as for the population quantile.
Conditional Quantile and Quantile Regression
Suppose the th conditional quantile function is
th conditional quantile function is 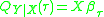 . Given the distribution function of
. Given the distribution function of 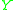 ,
, 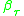 can be obtained by solving
can be obtained by solving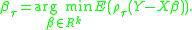
Solving the sample analog gives the estimator of
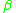 .
.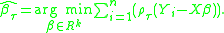
Computation
The minimization problem can be reformulated as a linear programmingLinear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
problem
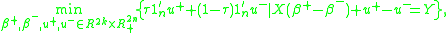
where
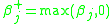 ,
,  ,
, 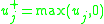 ,
, 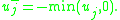
Simplex methods
Simplex algorithm
In mathematical optimization, Dantzig's simplex algorithm is a popular algorithm for linear programming. The journal Computing in Science and Engineering listed it as one of the top 10 algorithms of the twentieth century....
or interior point method
Interior point method
Interior point methods are a certain class of algorithms to solve linear and nonlinear convex optimization problems.The interior point method was invented by John von Neumann...
s can be applied to solve the linear programming problem.
Asymptotic properties
For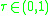 , under some regularity conditions,
, under some regularity conditions, 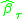 is asymptotically normal:
is asymptotically normal: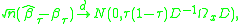
where
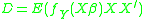 and
and 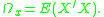
Scale equivariance
For any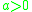 and
and 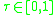
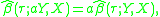
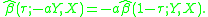
Shift equivariance
For any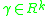 and
and 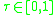
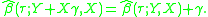
Equivariance to reparameterization of design
Let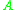 be any
be any 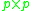 nonsingular matrix and
nonsingular matrix and 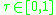
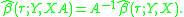
Invariance to monotone transformations
If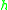 is a nondecreasing function on R, the following invariance
is a nondecreasing function on R, the following invarianceInvariant estimator
In statistics, the concept of being an invariant estimator is a criterion that can be used to compare the properties of different estimators for the same quantity. It is a way of formalising the idea that an estimator should have certain intuitively appealing qualities...
property applies:
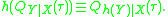
Example 1
Let
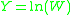 and
and 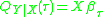 , then
, then 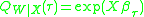 . The mean regression does not have the same property since
. The mean regression does not have the same property since 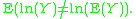
Example 2
Let
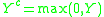 and
and 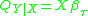 , then
, then 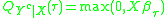 . This is the censored quantile regression model: estimated values can be obtained without making any distributional assumptions, but at the cost of computational difficulty, some of which can be avoided by using a simple three step censored quantile regression procedure as an approximation.
. This is the censored quantile regression model: estimated values can be obtained without making any distributional assumptions, but at the cost of computational difficulty, some of which can be avoided by using a simple three step censored quantile regression procedure as an approximation.Implementations
Some statistics packages, such as RR (programming language)
R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
, Eviews
EViews
EViews is a statistical package for Windows, used mainly for time-series oriented econometric analysis. It is developed by Quantitative Micro Software , now a part of IHS. Version 1.0 was released in March 1994, and replaced MicroTSP...
(ver. 6), Stata
Stata
Stata is a general-purpose statistical software package created in 1985 by StataCorp. It is used by many businesses and academic institutions around the world...
(via qreg), gretl
Gretl
gretl is an open-source statistical package, mainly for econometrics. The name is an acronym for Gnu Regression, Econometrics and Time-series Library. It has a graphical user interface and can be used together with X-12-ARIMA, TRAMO/SEATS, R, Octave, and Ox. It is written in C, uses GTK as widget...
, SAS
SAS System
SAS is an integrated system of software products provided by SAS Institute Inc. that enables programmers to perform:* retrieval, management, and mining* report writing and graphics* statistical analysis...
through proc quantreg (ver. 9.2), and RATS include implementations of quantile regression. R implements it through Roger Koenker's quantreg package.
External links
- Quantile LOWESS – A method to perform Local Quantile regression (with R code)

