Projective object
Encyclopedia
In category theory
, the notion of a projective object generalizes the notion of a projective module
.
An object P in a category C is projective if the hom functor
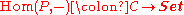
preserves epimorphism
s. That is, every morphism f:P→X factors through every epi Y→X.
Let
be an abelian category
. In this context, an object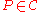
is called a projective object if
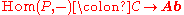
is an exact functor
, where
is the category
of abelian group
s.
The dual notion of a projective object is that of an injective object
: An object
in an abelian category 
is injective if the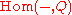 
functor
from
to 
is exact.
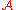be an abelian category
.
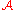is said to have enough projectives if, for every object 
of 
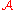, there is a projective object 
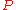of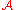 
and an exact sequence
In other words, the map
is "epi", or an epimorphism
.
be a ring
with 1. Consider the category of left
-modules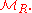 
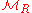is an abelian category. The projective objects in 
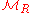are precisely the projective left R-modules
. So
is itself a projective object in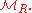 
Dually, the injective objects in 
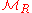are exactly the injective left R-modules
.
The category
of left (right)
-modules also has enough projectives. This is true since, for every left (right) 
-module 
, we can take 
to be the free (and hence projective) 
-module generated by a generating set 
for 
(we can in fact take 
to be 
). Then the canonical projection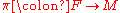 
is the required surjection.
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, the notion of a projective object generalizes the notion of a projective module
Projective module
In mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
.
An object P in a category C is projective if the hom functor
Hom functor
In mathematics, specifically in category theory, hom-sets, i.e. sets of morphisms between objects, give rise to important functors to the category of sets. These functors are called hom-functors and have numerous applications in category theory and other branches of mathematics.-Formal...
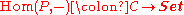
preserves epimorphism
Epimorphism
In category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
s. That is, every morphism f:P→X factors through every epi Y→X.
Let
be an abelian categoryAbelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
. In this context, an object
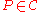is called a projective object if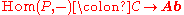is an exact functor
Exact functor
In homological algebra, an exact functor is a functor, from some category to another, which preserves exact sequences. Exact functors are very convenient in algebraic calculations, roughly speaking because they can be applied to presentations of objects easily...
, where
is the categoryCategory (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s.
The dual notion of a projective object is that of an injective object
Injective object
In mathematics, especially in the field of category theory, the concept of injective object is a generalization of the concept of injective module. This concept is important in homotopy theory and in theory of model categories...
: An object
in an abelian category is injective if the 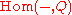functorHom functor
In mathematics, specifically in category theory, hom-sets, i.e. sets of morphisms between objects, give rise to important functors to the category of sets. These functors are called hom-functors and have numerous applications in category theory and other branches of mathematics.-Formal...
from
to is exact.Enough projectives
Let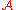 be an abelian categoryAbelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
.
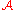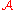is said to have enough projectives if, for every object of , there is a projective object 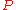of 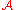and an exact sequenceExact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
In other words, the map
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
is "epi", or an epimorphismAbelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
.
Examples.
Let be a ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
with 1. Consider the category of left
-modules 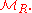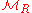is an abelian category. The projective objects in 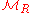are precisely the projective left R-modulesProjective module
In mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
. So
is itself a projective object in 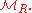Dually, the injective objects in 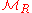are exactly the injective left R-modulesInjective module
In mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module Q that shares certain desirable properties with the Z-module Q of all rational numbers...
.
The category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of left (right)
-modules also has enough projectives. This is true since, for every left (right) -module , we can take to be the free (and hence projective) -module generated by a generating set for (we can in fact take to be ). Then the canonical projection 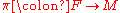is the required surjection.