Practical number
Encyclopedia
In number theory
, a practical number or panarithmic number is a positive integer n such that all smaller positive integers can be represented as sums of distinct divisor
s of n. For example, 12 is a practical number because all the numbers from 1 to 11 can be expressed as sums of its divisors 1, 2, 3, 4, and 6: as well as these divisors themselves, we have 5=3+2, 7=6+1, 8=6+2, 9=6+3, 10=6+3+1, and 11=6+3+2.
The sequence of practical numbers begins
Practical numbers were used by Fibonacci
in his Liber Abaci
(1202) in connection with the problem of representing rational numbers as Egyptian fractions. Fibonacci does not formally define practical numbers, but he gives a table of Egyptian fraction expansions for fractions with practical denominators.
The name "practical number" is due to , who first attempted a classification of these numbers that was completed by and . This characterization makes it possible to determine whether a number is practical by examining its prime factorization. Any even perfect number
and any power of two
is also a practical number.
Practical numbers have also been shown to be analogous with prime number
s in many of their properties.
A positive integer
with 
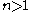and primes 
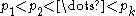is practical if and only if 
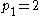and, for every i from 2 to k,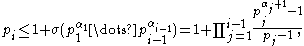
where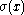
denotes the sum of the divisors
of x. For example, 3 ≤ σ(2)+1 = 4, 29 ≤ σ(2 × 32)+1 = 40, and 823 ≤ σ(2 × 32 × 29)+1=1171, so 2 × 32 × 29 × 823 = 429606 is practical. This characterization extends a partial classification of the practical numbers given by .
It is not difficult to prove that this condition is necessary and sufficient for a number to be practical. In one direction, this condition is clearly necessary in order to be able to represent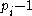
as a sum of divisors of n. In the other direction, the condition is sufficient, as can be shown by induction. More strongly, one can show that, if the factorization of n satisfies the condition above, then any 
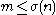can be represented as a sum of divisors of n, by the following sequence of steps:
is a practical number. Powers of two trivially satisfy the characterization of practical numbers in terms of their prime factorizations: the only prime in their factorizations, p1, equals two as required. Any even perfect number
is also a practical number: due to Euler's result that these numbers must have the form 2n − 1(2n − 1), every odd prime factor of an even perfect number must be at most the sum of the divisors of the even part of the number, and therefore the number must satisfy the characterization of practical numbers.
Any primorial
is practical. By Bertrand's postulate, each successive prime in the prime factorization of a primorial must be smaller than the product of the first and last primes in the factorization of the preceding primorial, so primorials necessarily satisfy the characterization of practical numbers. Therefore, also, any number that is the product of nonzero powers of the first k primes must also be practical; this includes Ramanujan's highly composite number
s (numbers with more divisors than any smaller positive integer) as well as the factorial
numbers.
of the form m/n may be represented as a sum ∑di/n where each di is a distinct divisor of n. Each term in this sum simplifies to a unit fraction
, so such a sum provides a representation of m/n as an Egyptian fraction. For instance,
Fibonacci, in his 1202 book Liber Abaci
lists several methods for finding Egyptian fraction representations of a rational number. Of these, the first is to test whether the number is itself already a unit fraction, but the second is to search for a representation of the numerator as a sum of divisors of the denominator, as described above; this method is only guaranteed to succeed for denominators that are practical. Fibonacci provides tables of these representations for fractions having as denominators the practical numbers 6, 8, 12, 20, 24, 60, and 100.
showed that every number x/y has an Egyptian fraction representation with
terms. The proof involves finding a sequence of practical numbers ni with the property that every number less than ni may be written as a sum of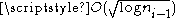 
distinct divisors of ni. Then, i is chosen so that ni − 1 < y ≤ ni, and xni is divided by y giving quotient q and remainder r. It follows from these choices that 
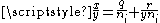. Expanding both numerators on the right hand side of this formula into sums of divisors of ni results in the desired Egyptian fraction representation. use a similar technique involving a different sequence of practical numbers to show that every number x/y has an Egyptian fraction representation in which the largest denominator is 
.
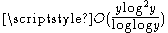a formula which resembles the prime number theorem
. This result largely resolved a conjecture of that p(x) is asymptotic to cx/log x for some constant c, and it strengthens an earlier claim of that the practical numbers have density zero in the integers.
Theorems analogous to Goldbach's conjecture
and the twin prime conjecture are also known for practical numbers: every positive even integer is the sum of two practical numbers, and there exist infinitely many triples of practical numbers x − 2, x, x + 2. Melfi also showed that there are infinitely many practical Fibonacci number
s ; the analogous question of the existence of infinitely many Fibonacci prime
s is open. showed that there always exists a practical number in the interval [x2,(x + 1)2] for any positive real x, a result analogous to Legendre's conjecture
for primes.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, a practical number or panarithmic number is a positive integer n such that all smaller positive integers can be represented as sums of distinct divisor
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
s of n. For example, 12 is a practical number because all the numbers from 1 to 11 can be expressed as sums of its divisors 1, 2, 3, 4, and 6: as well as these divisors themselves, we have 5=3+2, 7=6+1, 8=6+2, 9=6+3, 10=6+3+1, and 11=6+3+2.
The sequence of practical numbers begins
- 1, 2, 4, 6, 8, 12, 16, 18, 20, 24, 28, 30, 32, 36, 40, 42, 48, 54, ....
Practical numbers were used by Fibonacci
Fibonacci
Leonardo Pisano Bigollo also known as Leonardo of Pisa, Leonardo Pisano, Leonardo Bonacci, Leonardo Fibonacci, or, most commonly, simply Fibonacci, was an Italian mathematician, considered by some "the most talented western mathematician of the Middle Ages."Fibonacci is best known to the modern...
in his Liber Abaci
Liber Abaci
Liber Abaci is a historic book on arithmetic by Leonardo of Pisa, known later by his nickname Fibonacci...
(1202) in connection with the problem of representing rational numbers as Egyptian fractions. Fibonacci does not formally define practical numbers, but he gives a table of Egyptian fraction expansions for fractions with practical denominators.
The name "practical number" is due to , who first attempted a classification of these numbers that was completed by and . This characterization makes it possible to determine whether a number is practical by examining its prime factorization. Any even perfect number
Perfect number
In number theory, a perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself . Equivalently, a perfect number is a number that is half the sum of all of its positive divisors i.e...
and any power of two
Power of two
In mathematics, a power of two means a number of the form 2n where n is an integer, i.e. the result of exponentiation with as base the number two and as exponent the integer n....
is also a practical number.
Practical numbers have also been shown to be analogous with prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s in many of their properties.
Characterization of practical numbers
As and showed, it is straightforward to determine whether a number is practical from its prime factorization.A positive integer
with 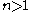and primes 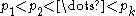is practical if and only if 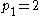and, for every i from 2 to k,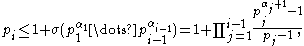where
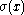denotes the sum of the divisorsDivisor function
In mathematics, and specifically in number theory, a divisor function is an arithmetical function related to the divisors of an integer. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships...
of x. For example, 3 ≤ σ(2)+1 = 4, 29 ≤ σ(2 × 32)+1 = 40, and 823 ≤ σ(2 × 32 × 29)+1=1171, so 2 × 32 × 29 × 823 = 429606 is practical. This characterization extends a partial classification of the practical numbers given by .
It is not difficult to prove that this condition is necessary and sufficient for a number to be practical. In one direction, this condition is clearly necessary in order to be able to represent
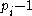as a sum of divisors of n. In the other direction, the condition is sufficient, as can be shown by induction. More strongly, one can show that, if the factorization of n satisfies the condition above, then any 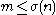can be represented as a sum of divisors of n, by the following sequence of steps:
- Let
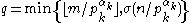, and let 
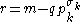. - Since
and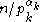 
can be shown by induction to be practical, we can find a representation of q as a sum of divisors of 
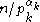. - Since
, and since 
can be shown by induction to be practical, we can find a representation of r as a sum of divisors of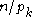 
. - The divisors representing r, together with
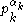times each of the divisors representing q, together form a representation of m as a sum of divisors of n.
Relation to other classes of numbers
Any power of twoPower of two
In mathematics, a power of two means a number of the form 2n where n is an integer, i.e. the result of exponentiation with as base the number two and as exponent the integer n....
is a practical number. Powers of two trivially satisfy the characterization of practical numbers in terms of their prime factorizations: the only prime in their factorizations, p1, equals two as required. Any even perfect number
Perfect number
In number theory, a perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself . Equivalently, a perfect number is a number that is half the sum of all of its positive divisors i.e...
is also a practical number: due to Euler's result that these numbers must have the form 2n − 1(2n − 1), every odd prime factor of an even perfect number must be at most the sum of the divisors of the even part of the number, and therefore the number must satisfy the characterization of practical numbers.
Any primorial
Primorial
In mathematics, and more particularly in number theory, primorial is a function from natural numbers to natural numbers similar to the factorial function, but rather than multiplying successive positive integers, only successive prime numbers are multiplied...
is practical. By Bertrand's postulate, each successive prime in the prime factorization of a primorial must be smaller than the product of the first and last primes in the factorization of the preceding primorial, so primorials necessarily satisfy the characterization of practical numbers. Therefore, also, any number that is the product of nonzero powers of the first k primes must also be practical; this includes Ramanujan's highly composite number
Highly composite number
A highly composite number is a positive integer with more divisors than any positive integer smaller than itself.The initial or smallest twenty-one highly composite numbers are listed in the table at right....
s (numbers with more divisors than any smaller positive integer) as well as the factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
numbers.
Practical numbers and Egyptian fractions
If n is practical, then any rational numberRational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
of the form m/n may be represented as a sum ∑di/n where each di is a distinct divisor of n. Each term in this sum simplifies to a unit fraction
Unit fraction
A unit fraction is a rational number written as a fraction where the numerator is one and the denominator is a positive integer. A unit fraction is therefore the reciprocal of a positive integer, 1/n...
, so such a sum provides a representation of m/n as an Egyptian fraction. For instance,
Fibonacci, in his 1202 book Liber Abaci
Liber Abaci
Liber Abaci is a historic book on arithmetic by Leonardo of Pisa, known later by his nickname Fibonacci...
lists several methods for finding Egyptian fraction representations of a rational number. Of these, the first is to test whether the number is itself already a unit fraction, but the second is to search for a representation of the numerator as a sum of divisors of the denominator, as described above; this method is only guaranteed to succeed for denominators that are practical. Fibonacci provides tables of these representations for fractions having as denominators the practical numbers 6, 8, 12, 20, 24, 60, and 100.
showed that every number x/y has an Egyptian fraction representation with
terms. The proof involves finding a sequence of practical numbers ni with the property that every number less than ni may be written as a sum of 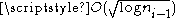distinct divisors of ni. Then, i is chosen so that ni − 1 < y ≤ ni, and xni is divided by y giving quotient q and remainder r. It follows from these choices that 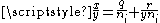. Expanding both numerators on the right hand side of this formula into sums of divisors of ni results in the desired Egyptian fraction representation. use a similar technique involving a different sequence of practical numbers to show that every number x/y has an Egyptian fraction representation in which the largest denominator is 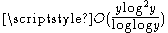.Analogies with prime numbers
One reason for interest in practical numbers is that many of their properties are similar to properties of the prime numbers. For example, if p(x) is the enumerating function of practical numbers, i.e., the number of practical numbers not exceeding x, proved that for suitable constants c1 and c2:a formula which resembles the prime number theorem
Prime number theorem
In number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
. This result largely resolved a conjecture of that p(x) is asymptotic to cx/log x for some constant c, and it strengthens an earlier claim of that the practical numbers have density zero in the integers.
Theorems analogous to Goldbach's conjecture
Goldbach's conjecture
Goldbach's conjecture is one of the oldest unsolved problems in number theory and in all of mathematics. It states:A Goldbach number is a number that can be expressed as the sum of two odd primes...
and the twin prime conjecture are also known for practical numbers: every positive even integer is the sum of two practical numbers, and there exist infinitely many triples of practical numbers x − 2, x, x + 2. Melfi also showed that there are infinitely many practical Fibonacci number
Fibonacci number
In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
s ; the analogous question of the existence of infinitely many Fibonacci prime
Fibonacci prime
A Fibonacci prime is a Fibonacci number that is prime, a type of integer sequence prime.The first Fibonacci primes are :-Known Fibonacci primes:It is not known if there are infinitely many Fibonacci primes...
s is open. showed that there always exists a practical number in the interval [x2,(x + 1)2] for any positive real x, a result analogous to Legendre's conjecture
Legendre's conjecture
Legendre's conjecture, proposed by Adrien-Marie Legendre, states that there is a prime number between n2 and 2 for every positive integer n. The conjecture is one of Landau's problems and unproven ....
for primes.
External links
- Tables of practical numbers compiled by Giuseppe Melfi