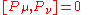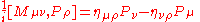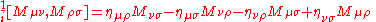Poincaré group
Encyclopedia
In physics
and mathematics
, the Poincaré group, named after Henri Poincaré
, is the group
of isometries
of Minkowski spacetime.
is a way in which the contents of spacetime could be shifted that would not affect the proper time
along a trajectory
between event
s. For example, if everything was postponed by two hours including two events and the path you took to go from one to the other, then the time interval between the events recorded by a stop-watch you carried with you would be the same. Or if everything was shifted five miles to the west, you would also see no change in the interval. It turns out that the length of a rod is also unaffected by such a shift.
If you ignore the effects of gravity, then there are ten basic ways of doing such shifts: translation through time, translation through any of the three dimensions of space, rotation (by a fixed angle) around any of the three spatial axes, or a boost
in any of the three spatial directions. 10=1+3+3+3. If you combine such isometries together (do one and then the other), the result is also such an isometry (although not generally one of the ten basic ones). These isometries form a group
. That is, there is an identity (no shift, everything stays where it was), and inverses (move everything back to where it was), and it obeys the associative law. The name of this particular group is the "Poincaré group".
of isometries
of Minkowski spacetime. It is a 10-dimensional noncompact
Lie group
. The abelian group
of translations
is a normal subgroup
while the Lorentz group
is a subgroup, the stabilizer of a point. That is, the full Poincaré group is the affine group
of the Lorentz group
, i.e. the Poincaré group is a semidirect product
of the translations and the Lorentz transformation
s:
Another way of putting it is that the Poincaré group is a group extension
of the Lorentz group
by a vector representation
of it.
Its positive energy unitary irreducible representations
are indexed by mass
(nonnegative number) and spin
(integer
or half integer), and are associated with particles in quantum mechanics
.
In accordance with the Erlangen program
, the geometry of Minkowski space is defined by the Poincaré group: Minkowski space is considered as a homogeneous space
for the group.
The Poincaré algebra is the Lie algebra
of the Poincaré group. In component form, the Poincaré algebra is given by the commutation relations:
where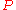 is the generator of translations,
is the generator of translations,  is the generator of Lorentz transformations and
is the generator of Lorentz transformations and  is the Minkowski metric (see sign convention
is the Minkowski metric (see sign convention
).
The Poincaré group is the full symmetry group of any relativistic field theory. As a result, all elementary particle
s fall in representations of this group. These are usually specified by the four-momentum of each particle (i.e. its mass) and the intrinsic quantum numbers JPC, where J is the spin
quantum number, P is the parity
and C is the charge conjugation quantum number. Many quantum field theories do violate parity and charge conjugation. In those cases, we drop the P and the C. Since CPT
is an invariance of every quantum field theory
, a time reversal quantum number could easily be constructed out of those given.
As a topological space, the group has four connected components: the component of the identity; the time reversed component; the spatial inversion component; and the component which is both time reversed and spatially inverted.
and includes
The last two symmetries together make up the Lorentz group
(see Lorentz invariance). These are generators of a Lie group
called the Poincaré group which is a semi-direct product of the group of translations and the Lorentz group. Things which are invariant under this group are said to have Poincaré invariance or relativistic invariance.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Poincaré group, named after Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
, is the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of isometries
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
of Minkowski spacetime.
Simple explanation
An isometryIsometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
is a way in which the contents of spacetime could be shifted that would not affect the proper time
Proper time
In relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
along a trajectory
Trajectory
A trajectory is the path that a moving object follows through space as a function of time. The object might be a projectile or a satellite, for example. It thus includes the meaning of orbit—the path of a planet, an asteroid or a comet as it travels around a central mass...
between event
Event (relativity)
In physics, and in particular relativity, an event indicates a physical situation or occurrence, located at a specific point in space and time. For example, a glass breaking on the floor is an event; it occurs at a unique place and a unique time, in a given frame of reference.Strictly speaking, the...
s. For example, if everything was postponed by two hours including two events and the path you took to go from one to the other, then the time interval between the events recorded by a stop-watch you carried with you would be the same. Or if everything was shifted five miles to the west, you would also see no change in the interval. It turns out that the length of a rod is also unaffected by such a shift.
If you ignore the effects of gravity, then there are ten basic ways of doing such shifts: translation through time, translation through any of the three dimensions of space, rotation (by a fixed angle) around any of the three spatial axes, or a boost
Lorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
in any of the three spatial directions. 10=1+3+3+3. If you combine such isometries together (do one and then the other), the result is also such an isometry (although not generally one of the ten basic ones). These isometries form a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. That is, there is an identity (no shift, everything stays where it was), and inverses (move everything back to where it was), and it obeys the associative law. The name of this particular group is the "Poincaré group".
Technical explanation
The Poincaré group is the groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of isometries
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
of Minkowski spacetime. It is a 10-dimensional noncompact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
. The abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
of translations
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
is a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
while the Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
is a subgroup, the stabilizer of a point. That is, the full Poincaré group is the affine group
Affine group
In mathematics, the affine group or general affine group of any affine space over a field K is the group of all invertible affine transformations from the space into itself.It is a Lie group if K is the real or complex field or quaternions....
of the Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
, i.e. the Poincaré group is a semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of the translations and the Lorentz transformation
Lorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
s:
Another way of putting it is that the Poincaré group is a group extension
Group extension
In mathematics, a group extension is a general means of describing a group in terms of a particular normal subgroup and quotient group. If Q and N are two groups, then G is an extension of Q by N if there is a short exact sequence...
of the Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
by a vector representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of it.
Its positive energy unitary irreducible representations
Representation of a Lie group
In mathematics and theoretical physics, the idea of a representation of a Lie group plays an important role in the study of continuous symmetry. A great deal is known about such representations, a basic tool in their study being the use of the corresponding 'infinitesimal' representations of Lie...
are indexed by mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
(nonnegative number) and spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
(integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
or half integer), and are associated with particles in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
.
In accordance with the Erlangen program
Erlangen program
An influential research program and manifesto was published in 1872 by Felix Klein, under the title Vergleichende Betrachtungen über neuere geometrische Forschungen...
, the geometry of Minkowski space is defined by the Poincaré group: Minkowski space is considered as a homogeneous space
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
for the group.
The Poincaré algebra is the Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of the Poincaré group. In component form, the Poincaré algebra is given by the commutation relations:
where
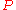 is the generator of translations,
is the generator of translations,  is the generator of Lorentz transformations and
is the generator of Lorentz transformations and  is the Minkowski metric (see sign convention
is the Minkowski metric (see sign conventionSign convention
In physics, a sign convention is a choice of the physical significance of signs for a set of quantities, in a case where the choice of sign is arbitrary. "Arbitrary" here means that the same physical system can be correctly described using different choices for the signs, as long as one set of...
).
The Poincaré group is the full symmetry group of any relativistic field theory. As a result, all elementary particle
Elementary particle
In particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...
s fall in representations of this group. These are usually specified by the four-momentum of each particle (i.e. its mass) and the intrinsic quantum numbers JPC, where J is the spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
quantum number, P is the parity
Parity (physics)
In physics, a parity transformation is the flip in the sign of one spatial coordinate. In three dimensions, it is also commonly described by the simultaneous flip in the sign of all three spatial coordinates:...
and C is the charge conjugation quantum number. Many quantum field theories do violate parity and charge conjugation. In those cases, we drop the P and the C. Since CPT
CPT symmetry
CPT symmetry is a fundamental symmetry of physical laws under transformations that involve the inversions of charge, parity, and time simultaneously.-History:...
is an invariance of every quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, a time reversal quantum number could easily be constructed out of those given.
As a topological space, the group has four connected components: the component of the identity; the time reversed component; the spatial inversion component; and the component which is both time reversed and spatially inverted.
Poincaré symmetry
Poincaré symmetry is the full symmetry of special relativitySpecial relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
and includes
- translationsTranslation (physics)In physics, translation is movement that changes the position of an object, as opposed to rotation. For example, according to Whittaker:...
(i.e., displacements) in time and space (these form the abelianAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
of translations on space-time) - rotationRotationA rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
s in space (this forms the non-Abelian Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
of 3-dimensional rotations) - boosts, i.e., transformations connecting two uniformly moving bodies.
The last two symmetries together make up the Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
(see Lorentz invariance). These are generators of a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
called the Poincaré group which is a semi-direct product of the group of translations and the Lorentz group. Things which are invariant under this group are said to have Poincaré invariance or relativistic invariance.
See also
- Euclidean groupEuclidean groupIn mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
- Representation theory of the Poincaré groupRepresentation theory of the Poincaré groupIn mathematics, the representation theory of the Poincaré group is an example of the representation theory of a Lie group that is neither a compact group nor a semisimple group. It is fundamental in theoretical physics....
- Wigner's classificationWigner's classificationIn mathematics and theoretical physics, Wigner's classificationis a classification of the nonnegative energy irreducible unitary representations of the Poincaré group, which have sharp mass eigenvalues...