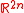Parabolic geometry (differential geometry)
Encyclopedia
In differential geometry and the study of Lie group
s, a parabolic geometry is a homogeneous space
G/P which is the quotient of a semisimple Lie group G by a parabolic subgroup P. More generally, the curved analogs of a parabolic geometry in this sense is also called a parabolic geometry: any geometry that is modeled on such a space by means of a Cartan connection
.
Pn is an example. It is the homogeneous space PGL(n+1)/H where H is the isotropy group of a line. In this geometrical space, the notion of a straight line is meaningful, but there is no preferred ("affine") parameter along the lines. The curved analog of projective space is a manifold in which the notion of a geodesic
makes sense, but for which there are no preferred parametrizations on those geodesics. A projective connection
is the relevant Cartan connection that gives a means for describing a projective geometry by gluing copies of the projective space to the tangent spaces of the base manifold. Broadly speaking, projective geometry
refers to the study of manifolds with this kind of connection.
Another example is the conformal sphere
. Topologically, it is the n-sphere, but there is no notion of length defined on it, just of angle between curves. Equivalently, this geometry is described as an equivalence class of Riemannian metrics on the sphere (called a conformal class). The group of transformations that preserve angles on the sphere is the Lorentz group
O(n+1,1), and so Sn = O(n+1,1)/P. Conformal geometry
is, more broadly, the study of manifolds with a conformal equivalence class of Riemannian metrics, i.e., manifolds modeled on the conformal sphere. Here the associated Cartan connection is the conformal connection
.
Other examples include:
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s, a parabolic geometry is a homogeneous space
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
G/P which is the quotient of a semisimple Lie group G by a parabolic subgroup P. More generally, the curved analogs of a parabolic geometry in this sense is also called a parabolic geometry: any geometry that is modeled on such a space by means of a Cartan connection
Cartan connection
In the mathematical field of differential geometry, a Cartan connection is a flexible generalization of the notion of an affine connection. It may also be regarded as a specialization of the general concept of a principal connection, in which the geometry of the principal bundle is tied to the...
.
Examples
The projective spaceProjective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
Pn is an example. It is the homogeneous space PGL(n+1)/H where H is the isotropy group of a line. In this geometrical space, the notion of a straight line is meaningful, but there is no preferred ("affine") parameter along the lines. The curved analog of projective space is a manifold in which the notion of a geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
makes sense, but for which there are no preferred parametrizations on those geodesics. A projective connection
Projective connection
In differential geometry, a projective connection is a type of Cartan connection on a differentiable manifold.The structure of a projective connection is modeled on the geometry of projective space, rather than the affine space corresponding to an affine connection. Much like affine connections,...
is the relevant Cartan connection that gives a means for describing a projective geometry by gluing copies of the projective space to the tangent spaces of the base manifold. Broadly speaking, projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
refers to the study of manifolds with this kind of connection.
Another example is the conformal sphere
Conformal geometry
In mathematics, conformal geometry is the study of the set of angle-preserving transformations on a space. In two real dimensions, conformal geometry is precisely the geometry of Riemann surfaces...
. Topologically, it is the n-sphere, but there is no notion of length defined on it, just of angle between curves. Equivalently, this geometry is described as an equivalence class of Riemannian metrics on the sphere (called a conformal class). The group of transformations that preserve angles on the sphere is the Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
O(n+1,1), and so Sn = O(n+1,1)/P. Conformal geometry
Conformal geometry
In mathematics, conformal geometry is the study of the set of angle-preserving transformations on a space. In two real dimensions, conformal geometry is precisely the geometry of Riemann surfaces...
is, more broadly, the study of manifolds with a conformal equivalence class of Riemannian metrics, i.e., manifolds modeled on the conformal sphere. Here the associated Cartan connection is the conformal connection
Conformal connection
In conformal differential geometry, a conformal connection is a Cartan connection on an n-dimensional manifold M arising as a deformation of the Klein geometry given by the celestial n-sphere, viewed as the homogeneous space...
.
Other examples include:
- CR geometry, the study of manifolds modeled on a real hyperquadric
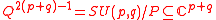 , where
, where 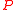 is the stabilizer of an isotropic line (see CR manifoldCR manifoldIn mathematics, a CR manifold is a differentiable manifold together with a geometric structure modeled on that of a real hypersurface in a complex vector space, or more generally modeled on an edge of a wedge....
is the stabilizer of an isotropic line (see CR manifoldCR manifoldIn mathematics, a CR manifold is a differentiable manifold together with a geometric structure modeled on that of a real hypersurface in a complex vector space, or more generally modeled on an edge of a wedge....
)
- contact projective geometry, the study of manifolds modeled on
 where
where 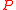 is that subgroup of the symplectic groupSymplectic groupIn mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...
is that subgroup of the symplectic groupSymplectic groupIn mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...
stabilizing the line generated by the first standard basis vector in