Malgrange–Ehrenpreis theorem
Encyclopedia
In mathematics, the Malgrange–Ehrenpreis theorem states that every non-zero linear differential operator
with constant coefficients
has a Green's function
. It was first proved independently by and
.
This means that if P is a polynomial (in several variables) then the differential equation
has a distributional
solution u, where δ is the Dirac delta function
. It can be used to show that
has a solution for any distribution f. The solution is not unique in general.
The analogue for differential operators whose coefficients are polynomials (rather than constants) is false: see Lewy's example
.
. Since then several constructive proof have been found.
There is a very short proof using the Fourier transform and the Bernstein–Sato polynomial
, as follows. By taking Fourier transform
s the Malgrange–Ehrenpreis theorem is equivalent to the fact that every non-zero polynomial P has a distributional inverse. By replacing P by the product with its complex conjugate, one can also assume that P is non-negative. For non-negative polynomials P the existence of a distributional inverse follows from the existence of the Bernstein–Sato polynomial, which implies that Ps can be analytically continued as a meromorphic distribution-valued function of the complex variable s; the constant term of the Laurent expansion of Ps at s = −1 is then a distributional inverse of P.
Other proofs, often giving better bounds on the growth of a solution, are given in , and .
gives a detailed discussion of the regularity properties of the fundamental solutions.
A short constructive proof was presented in
:
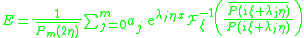
is a fundamental solution of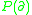
, i.e., 
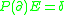, if
is the principal part of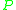 
, 
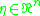with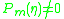 
, the real numbers 
are pairwise different,
and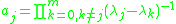
.
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
with constant coefficients
Constant coefficients
In mathematics, constant coefficients is a term applied to differential operators, and also some difference operators, to signify that they contain no functions of the independent variables, other than constant functions. In other words, it singles out special operators, within the larger class of...
has a Green's function
Green's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
. It was first proved independently by and
.
This means that if P is a polynomial (in several variables) then the differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
has a distributional
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
solution u, where δ is the Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
. It can be used to show that
has a solution for any distribution f. The solution is not unique in general.
The analogue for differential operators whose coefficients are polynomials (rather than constants) is false: see Lewy's example
Lewy's example
In the mathematical study of partial differential equations, Lewy's example is a celebrated example, due to Hans Lewy, of a linear partial differential equation with no solutions...
.
Proofs
The original proofs of Malgrange and Ehrenpreis were non-constructive as they used the Hahn–Banach theoremHahn–Banach theorem
In mathematics, the Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed...
. Since then several constructive proof have been found.
There is a very short proof using the Fourier transform and the Bernstein–Sato polynomial
Bernstein–Sato polynomial
In mathematics, the Bernstein–Sato polynomial is a polynomial related to differential operators, introduced independently by and , . It is also known as the b-function, the b-polynomial, and the Bernstein polynomial, though it is not related to the Bernstein polynomials used in approximation...
, as follows. By taking Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
s the Malgrange–Ehrenpreis theorem is equivalent to the fact that every non-zero polynomial P has a distributional inverse. By replacing P by the product with its complex conjugate, one can also assume that P is non-negative. For non-negative polynomials P the existence of a distributional inverse follows from the existence of the Bernstein–Sato polynomial, which implies that Ps can be analytically continued as a meromorphic distribution-valued function of the complex variable s; the constant term of the Laurent expansion of Ps at s = −1 is then a distributional inverse of P.
Other proofs, often giving better bounds on the growth of a solution, are given in , and .
gives a detailed discussion of the regularity properties of the fundamental solutions.
A short constructive proof was presented in
:
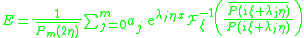
is a fundamental solution of
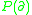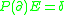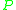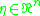, i.e., , if is the principal part of , with 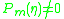, the real numbers are pairwise different,and
.
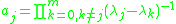