
Lemniscate of Bernoulli
Encyclopedia

Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the lemniscate of Bernoulli is a plane curve defined from two given points F1 and F2, known as foci, at distance 2a from each other as the locus of points P so that PF1·PF2 = a2. The curve has a shape similar to the numeral 8 and to the ∞
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
symbol. Its name is from lemniscus, which is Latin
Latin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
for "pendant ribbon". It is a special case of the Cassini oval
Cassini oval
A Cassini oval is a plane curve defined as the set of points in the plane such that the product of the distances to two fixed points is constant. This is related to an ellipse, for which the...
and is a rational algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
of degree 4.
The lemniscate was first described in 1694 by Jakob Bernoulli as a modification of an ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
, which is the locus
Locus (mathematics)
In geometry, a locus is a collection of points which share a property. For example a circle may be defined as the locus of points in a plane at a fixed distance from a given point....
of points for which the sum of the distance
Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
s to each of two fixed focal points is a constant
Mathematical constant
A mathematical constant is a special number, usually a real number, that is "significantly interesting in some way". Constants arise in many different areas of mathematics, with constants such as and occurring in such diverse contexts as geometry, number theory and calculus.What it means for a...
. A Cassini oval
Cassini oval
A Cassini oval is a plane curve defined as the set of points in the plane such that the product of the distances to two fixed points is constant. This is related to an ellipse, for which the...
, by contrast, is the locus of points for which the product of these distances is constant. In the case where the curve passes through the point midway between the foci, the oval is a lemniscate of Bernoulli.
This lemniscate
Lemniscate
In algebraic geometry, a lemniscate refers to any of several figure-eight or ∞ shaped curves. It may refer to:*The lemniscate of Bernoulli, often simply called the lemniscate, the locus of points whose product of distances from two foci equals the square of half the interfocal distance*The...
can be obtained as the inverse transform of a hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
, with the inversion circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
centered at the center of the hyperbola (bisector of its two foci). It may also be drawn by a mechanical linkage in the form of Watt's linkage
Watt's linkage
Watt's linkage is a type of mechanical linkage invented by James Watt in which the central moving point of the linkage is constrained to travel on an approximation to a straight line...
, with the lengths of the three bars of the linkage and the distance between its endpoints chosen to form a crossed square
Antiparallelogram
An antiparallelogram is a quadrilateral in which, like a parallelogram, the pairs of nonadjacent sides are congruent, but in which two opposite sides intersect and are therefore not parallel.-Properties:Every antiparallelogram has an axis of symmetry through its crossing point...
.
Equations
- Its CartesianCartesian coordinate systemA Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
equationEquationAn equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
is (up to translation and rotation):
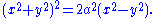
- In polar coordinates:
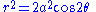 .
.- As parametric equationParametric equationIn mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....
:
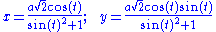
In two-center bipolar coordinates
Two-center bipolar coordinates
In mathematics, two-center bipolar coordinates is a coordinate system, based on two coordinates which give distances from two fixed centers, C1 and C2 This system is very useful in some scientific applications It should not be confused with so-called bipolar coordinates.-Cartesian...
:
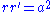
Derivatives
Each first derivative below was calculated using implicit differentiation.With y as a function of x
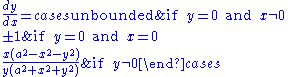
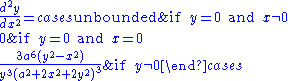
With x as a function of y
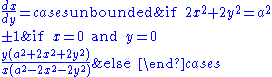
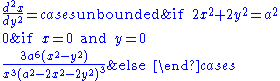
Curvature
Once the first two derivatives are known, curvature is easily calculated: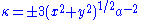
the sign being chosen according to the direction of motion along the curve. The lemniscate has the property that the magnitude of the curvature at any point is proportional to that point's distance from the origin.
Arc length and elliptic functions
The determination of the arc lengthArc length
Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
of arcs of the lemniscate leads to elliptic integral
Elliptic integral
In integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...
s, as was discovered in the eighteenth century. Around 1800, the elliptic function
Elliptic function
In complex analysis, an elliptic function is a function defined on the complex plane that is periodic in two directions and at the same time is meromorphic...
s inverting those integrals were studied by C. F. Gauss (largely unpublished at the time, but allusions in the notes to his Disquisitiones Arithmeticae
Disquisitiones Arithmeticae
The Disquisitiones Arithmeticae is a textbook of number theory written in Latin by Carl Friedrich Gauss in 1798 when Gauss was 21 and first published in 1801 when he was 24...
). The period lattices are of a very special form, being proportional to the Gaussian integer
Gaussian integer
In number theory, a Gaussian integer is a complex number whose real and imaginary part are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as Z[i]. The Gaussian integers are a special case of the quadratic...
s. For this reason the case of elliptic functions with complex multiplication
Complex multiplication
In mathematics, complex multiplication is the theory of elliptic curves E that have an endomorphism ring larger than the integers; and also the theory in higher dimensions of abelian varieties A having enough endomorphisms in a certain precise sense In mathematics, complex multiplication is the...
by the square root of minus one is called the lemniscatic case in some sources.
See also
- Lemniscate of Booth
- Lemniscate of GeronoLemniscate of GeronoIn algebraic geometry, the lemniscate of Gerono, or lemnicate of Huygens, or figure-eight curve, is a plane algebraic curve of degree four and genus zero shaped like an \infty symbol, or figure eight...
- Gauss's constantGauss's constantIn mathematics, Gauss's constant, denoted by G, is defined as the reciprocal of the arithmetic-geometric mean of 1 and the square root of 2:The constant is named after Carl Friedrich Gauss, who on May 30, 1799 discovered thatso that...
- Lemniscatic elliptic functionLemniscatic elliptic functionIn mathematics, and in particular the study of Weierstrass elliptic functions, the lemniscatic case occurs when the Weierstrass invariants satisfy g2=1 and g3=0...

