Lefschetz theorem on (1,1)-classes
Encyclopedia
In algebraic geometry
, a branch of mathematics
, the Lefschetz theorem on (1,1)-classes, named after Solomon Lefschetz
, is a classical statement relating divisor
s on a compact
Kähler manifold
to classes in its integral cohomology
. It is the only case of the Hodge conjecture
which has been proved for all Kähler manifolds.
c1 from linear equivalence classes of divisors to . By Hodge theory
, the de Rham cohomology
group H2(X, C) decomposes as a direct sum , and it can be proved that the image of the cycle class map lies in H1,1(X). The theorem says that the map to is surjective.
JCt (if a curve is singular, there is an appropriate generalized Jacobian variety). These can be assembled into a family
, the Jacobian of the pencil, which comes with a projection map π to the base T of the pencil. A normal function is a (holomorphic) section of π.
Fix an embedding of X in PN, and choose a pencil of curves Ct on X. For a fixed curve Γ on X, the intersection of Γ and Ct is a divisor on Ct, where d is the degree of X. Fix a base point p0 of the pencil. Then the divisor is a divisor of degree zero, and consequently it determines a class νΓ(t) in the Jacobian JCt for all t. The map from t to νΓ(t) is a normal function.
Henri Poincaré
proved that for a general pencil of curves, all normal functions arose as νΓ(t) for some choice of Γ. Lefschetz proved that any normal function determined a class in H2(X, Z) and that the class of νΓ is the fundamental class of Γ. Furthermore, he proved that a class in H2(X, Z) is the class of a normal function if and only if it lies in H1,1. Together with Poincaré's existence theorem, this proves the theorem on (1,1)-classes.
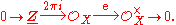
Taking sheaf cohomology of this exact sequence gives maps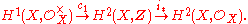
The group of linear equivalence classes of divisors is isomorphic to the group of line bundle
s on X, and this group is isomorphic to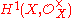
. The first Chern class map is c1 by definition, so it suffices to show that i* is zero.
Because X is Kähler, Hodge theory implies that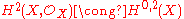
. However, i* factors through the map from H2(X, Z) to H2(X, C), and on H2(X, C), i* is the restriction of the projection onto H0,2(X). It follows that it is zero on , and consequently that the cycle class map is surjective.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Lefschetz theorem on (1,1)-classes, named after Solomon Lefschetz
Solomon Lefschetz
Solomon Lefschetz was an American mathematician who did fundamental work on algebraic topology, its applications to algebraic geometry, and the theory of non-linear ordinary differential equations.-Life:...
, is a classical statement relating divisor
Divisor (algebraic geometry)
In algebraic geometry, divisors are a generalization of codimension one subvarieties of algebraic varieties; two different generalizations are in common use, Cartier divisors and Weil divisors...
s on a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Kähler manifold
Kähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
to classes in its integral cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
. It is the only case of the Hodge conjecture
Hodge conjecture
The Hodge conjecture is a major unsolved problem in algebraic geometry which relates the algebraic topology of a non-singular complex algebraic variety and the subvarieties of that variety. More specifically, the conjecture says that certain de Rham cohomology classes are algebraic, that is, they...
which has been proved for all Kähler manifolds.
Statement of the theorem
Let X be a compact Kähler manifold. There is a cycle class map that takes a divisor class to a cohomology class. In this case, it is the first Chern classChern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
c1 from linear equivalence classes of divisors to . By Hodge theory
Hodge theory
In mathematics, Hodge theory, named after W. V. D. Hodge, is one aspect of the study of the algebraic topology of a smooth manifold M. More specifically, it works out the consequences for the cohomology groups of M, with real coefficients, of the partial differential equation theory of generalised...
, the de Rham cohomology
De Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
group H2(X, C) decomposes as a direct sum , and it can be proved that the image of the cycle class map lies in H1,1(X). The theorem says that the map to is surjective.
Proof using normal functions
Lefschetz's original proof worked on projective surfaces and used normal functions, which were introduced by Poincaré. Suppose that Ct is a pencil of curves on X. Each of these curves has a Jacobian varietyJacobian variety
In mathematics, the Jacobian variety J of a non-singular algebraic curve C of genus g is the moduli space of degree 0 line bundles...
JCt (if a curve is singular, there is an appropriate generalized Jacobian variety). These can be assembled into a family
, the Jacobian of the pencil, which comes with a projection map π to the base T of the pencil. A normal function is a (holomorphic) section of π.Fix an embedding of X in PN, and choose a pencil of curves Ct on X. For a fixed curve Γ on X, the intersection of Γ and Ct is a divisor on Ct, where d is the degree of X. Fix a base point p0 of the pencil. Then the divisor is a divisor of degree zero, and consequently it determines a class νΓ(t) in the Jacobian JCt for all t. The map from t to νΓ(t) is a normal function.
Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
proved that for a general pencil of curves, all normal functions arose as νΓ(t) for some choice of Γ. Lefschetz proved that any normal function determined a class in H2(X, Z) and that the class of νΓ is the fundamental class of Γ. Furthermore, he proved that a class in H2(X, Z) is the class of a normal function if and only if it lies in H1,1. Together with Poincaré's existence theorem, this proves the theorem on (1,1)-classes.
Proof using sheaf cohomology
Because X is a complex manifold, it admits an exponential sheaf sequenceExponential sheaf sequence
In mathematics, the exponential sheaf sequence is a fundamental short exact sequence of sheaves used in complex geometry.Let M be a complex manifold, and write OM for the sheaf of holomorphic functions on M. Let OM* be the subsheaf consisting of the non-vanishing holomorphic functions. These are...
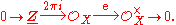
Taking sheaf cohomology of this exact sequence gives maps
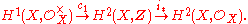
The group of linear equivalence classes of divisors is isomorphic to the group of line bundle
Line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
s on X, and this group is isomorphic to
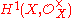. The first Chern class map is c1 by definition, so it suffices to show that i* is zero.Because X is Kähler, Hodge theory implies that
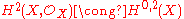. However, i* factors through the map from H2(X, Z) to H2(X, C), and on H2(X, C), i* is the restriction of the projection onto H0,2(X). It follows that it is zero on , and consequently that the cycle class map is surjective.