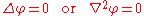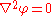Laplace's equation
Encyclopedia
In mathematics
, Laplace's equation is a second-order partial differential equation
named after Pierre-Simon Laplace
who first studied its properties. This is often written as:
where ∆ = ∇² is the Laplace operator
and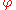 is a scalar function. In general, ∆ = ∇² is the Laplace–Beltrami or Laplace–de Rham operator.
is a scalar function. In general, ∆ = ∇² is the Laplace–Beltrami or Laplace–de Rham operator.
Laplace's equation and Poisson's equation
are the simplest examples of elliptic partial differential equations. Solutions of Laplace's equation are called harmonic function
s.
The general theory of solutions to Laplace's equation is known as potential theory
. The solutions of Laplace's equation are all harmonic function
s and are important in many fields of science, notably the fields of electromagnetism
, astronomy
, and fluid dynamics
, because they can be used to accurately describe the behavior of electric, gravitational, and fluid potential
s. In the study of heat conduction
, the Laplace equation is the steady-state heat equation
.
 , of real variables x, y, and z, such that
, of real variables x, y, and z, such that
In Cartesian coordinates
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Laplace's equation is a second-order partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
named after Pierre-Simon Laplace
Pierre-Simon Laplace
Pierre-Simon, marquis de Laplace was a French mathematician and astronomer whose work was pivotal to the development of mathematical astronomy and statistics. He summarized and extended the work of his predecessors in his five volume Mécanique Céleste...
who first studied its properties. This is often written as:
where ∆ = ∇² is the Laplace operator
Laplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
and
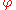 is a scalar function. In general, ∆ = ∇² is the Laplace–Beltrami or Laplace–de Rham operator.
is a scalar function. In general, ∆ = ∇² is the Laplace–Beltrami or Laplace–de Rham operator.Laplace's equation and Poisson's equation
Poisson's equation
In mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in electrostatics, mechanical engineering and theoretical physics...
are the simplest examples of elliptic partial differential equations. Solutions of Laplace's equation are called harmonic function
Harmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
s.
The general theory of solutions to Laplace's equation is known as potential theory
Potential theory
In mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
. The solutions of Laplace's equation are all harmonic function
Harmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
s and are important in many fields of science, notably the fields of electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
, astronomy
Astronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
, and fluid dynamics
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, because they can be used to accurately describe the behavior of electric, gravitational, and fluid potential
Potential
*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
s. In the study of heat conduction
Heat conduction
In heat transfer, conduction is a mode of transfer of energy within and between bodies of matter, due to a temperature gradient. Conduction means collisional and diffusive transfer of kinetic energy of particles of ponderable matter . Conduction takes place in all forms of ponderable matter, viz....
, the Laplace equation is the steady-state heat equation
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
.
Definition
In three dimensions, the problem is to find twice-differentiable real-valued functions , of real variables x, y, and z, such that
, of real variables x, y, and z, such thatIn Cartesian coordinates
-
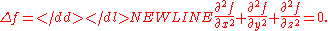
In cylindrical coordinates,
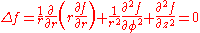
In spherical coordinates,
-

This is often written as
or, especially in more general contexts,
where ∆ = ∇² is the Laplace operatorLaplace operatorIn mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
or "Laplacian"
where ∇ ⋅ = div is the divergenceDivergenceIn vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
, and ∇ = grad is the gradientGradientIn vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
.
If the right-hand side is specified as a given function, f(x, y, z), i.e., if the whole equation is written as
then it is called "Poisson's equationPoisson's equationIn mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in electrostatics, mechanical engineering and theoretical physics...
".
The Laplace equation is also a special case of the Helmholtz equationHelmholtz equationThe Helmholtz equation, named for Hermann von Helmholtz, is the elliptic partial differential equation\nabla^2 A + k^2 A = 0where ∇2 is the Laplacian, k is the wavenumber, and A is the amplitude.-Motivation and uses:...
.
Laplace's equation and Poisson's equation are the simplest examples of elliptic partial differential equations.
Boundary conditions
The Dirichlet problemDirichlet problemIn mathematics, a Dirichlet problem is the problem of finding a function which solves a specified partial differential equation in the interior of a given region that takes prescribed values on the boundary of the region....
for Laplace's equation consists of finding a solution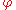 on some domain
on some domain  such that
such that 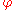 on the boundary of
on the boundary of  is equal to some given function. Since the Laplace operator appears in the heat equationHeat equationThe heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
is equal to some given function. Since the Laplace operator appears in the heat equationHeat equationThe heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
, one physical interpretation of this problem is as follows: fix the temperature on the boundary of the domain according to the given specification of the boundary condition. Allow heat to flow until a stationary state is reached in which the temperature at each point on the domain doesn't change anymore. The temperature distribution in the interior will then be given by the solution to the corresponding Dirichlet problem.
The Neumann boundary conditionNeumann boundary conditionIn mathematics, the Neumann boundary condition is a type of boundary condition, named after Carl Neumann.When imposed on an ordinary or a partial differential equation, it specifies the values that the derivative of a solution is to take on the boundary of the domain.* For an ordinary...
s for Laplace's equation specify not the function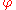 itself on the boundary of
itself on the boundary of  , but its normal derivative. Physically, this corresponds to the construction of a potential for a vector field whose effect is known at the boundary of
, but its normal derivative. Physically, this corresponds to the construction of a potential for a vector field whose effect is known at the boundary of  alone.
alone.
Solutions of Laplace's equation are called harmonic functionHarmonic functionIn mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
s; they are all analyticAnalytic functionIn mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
within the domain where the equation is satisfied. If any two functions are solutions to Laplace's equation (or any linear homogeneous differential equation), their sum (or any linear combination) is also a solution. This property, called the principle of superpositionSuperposition principleIn physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
, is very useful, e.g., solutions to complex problems can be constructed by summing simple solutions.
Laplace equation in two dimensions
The Laplace equation in two independent variables has the form

Analytic functions
The real and imaginary parts of a complex analytic functionAnalytic functionIn mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
both satisfy the Laplace equation. That is, if z = x + iy, and if
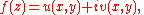
then the necessary condition that f(z) be analytic is that the Cauchy-Riemann equationsCauchy-Riemann equationsIn mathematics, the Cauchy–Riemann differential equations in complex analysis, named after Augustin Cauchy and Bernhard Riemann, consist of a system of two partial differential equations which must be satisfied if we know that a complex function is complex differentiable...
be satisfied:
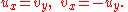
where ux is the first partial derivative of u with respect to x.
It follows that
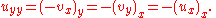
Therefore u satisfies the Laplace equation. A similar calculation shows that v also satisfies the Laplace equation.
Conversely, given a harmonic function, it is the real part of an analytic function, (at least locally). If a trial form is
(at least locally). If a trial form is
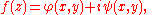
then the Cauchy-Riemann equations will be satisfied if we set

This relation does not determine ψ, but only its increments:
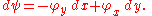
The Laplace equation for φ implies that the integrability condition for ψ is satisfied:
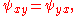
and thus ψ may be defined by a line integral. The integrability condition and Stokes' theoremStokes' theoremIn differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
implies that the value of the line integral connecting two points is independent of the path. The resulting pair of solutions of the Laplace equation are called conjugate harmonic functions. This construction is only valid locally, or provided that the path does not loop around a singularity. For example, if r and θ are polar coordinates and

then a corresponding analytic function is
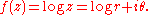
However, the angle θ is single-valued only in a region that does not enclose the origin.
The close connection between the Laplace equation and analytic functions implies that any solution of the Laplace equation has derivatives of all orders, and can be expanded in a power series, at least inside a circle that does not enclose a singularity. This is in sharp contrast to solutions of the wave equationWave equationThe wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
, which generally have less regularity.
There is an intimate connection between power series and Fourier seriesFourier seriesIn mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
. If we expand a function f in a power series inside a circle of radius R, this means that
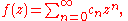
with suitably defined coefficients whose real and imaginary parts are given by

Therefore
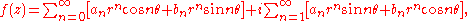
which is a Fourier series for f. These trigonometric functions can themselves be expanded, using multiple angle formulae.
Fluid flow
Let the quantities u and v be the horizontal and vertical components of the velocity field of a steady incompressible, irrotational flow in two dimensions. The condition that the flow be incompressible is that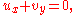
and the condition that the flow be irrotational is that

If we define the differential of a function ψ by
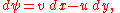
then the incompressibility condition is the integrability condition for this differential: the resulting function is called the stream functionStream functionThe stream function is defined for two-dimensional flows of various kinds. The stream function can be used to plot streamlines, which represent the trajectories of particles in a steady flow. Streamlines are perpendicular to equipotential lines...
because it is constant along flow linesStreamlines, streaklines and pathlinesFluid flow is characterized by a velocity vector field in three-dimensional space, within the framework of continuum mechanics. Streamlines, streaklines and pathlines are field lines resulting from this vector field description of the flow...
. The first derivatives of ψ are given by

and the irrotationality condition implies that ψ satisfies the Laplace equation. The harmonic function φ that is conjugate to ψ is called the velocity potential. The Cauchy-Riemann equations imply that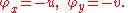
Thus every analytic function corresponds to a steady incompressible, irrotational fluid flow in the plane. The real part is the velocity potential, and the imaginary part is the stream function.
Electrostatics
According to Maxwell's equationsMaxwell's equationsMaxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
, an electric field (u,v) in two space dimensions that is independent of time satisfies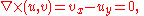
and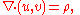
where ρ is the charge density. The first Maxwell equation is the integrability condition for the differential

so the electric potential φ may be constructed to satisfy
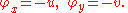
The second of Maxwell's equations then implies that

which is the Poisson equation.
It is important to note that the Laplace equation can be used in three-dimensional problems in electrostatics and fluid flow just as in two dimensions.
Fundamental solution
A fundamental solutionFundamental solutionIn mathematics, a fundamental solution for a linear partial differential operator L is a formulation in the language of distribution theory of the older idea of a Green's function...
of Laplace's equation satisfies
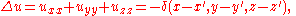
where the Dirac delta functionDirac delta functionThe Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
 denotes a unit source concentrated at the point
denotes a unit source concentrated at the point 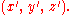
No function has this property, but it can be thought of as a limit of functions whose integrals over space are unity, and whose support (the region where the function is non-zero) shrinks to a point (see weak solutionWeak solutionIn mathematics, a weak solution to an ordinary or partial differential equation is a function for which the derivatives may not all exist but which is nonetheless deemed to satisfy the equation in some precisely defined sense. There are many different definitions of weak solution, appropriate for...
). It is common to take a different sign convention for this equation than one typically does when defining fundamental solutions. This choice of sign is often convenient to work with because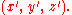 is a positive operator. The definition of the fundamental solution thus implies that, if the Laplacian of u is integrated over any volume that encloses the source point, then
is a positive operator. The definition of the fundamental solution thus implies that, if the Laplacian of u is integrated over any volume that encloses the source point, then

The Laplace equation is unchanged under a rotation of coordinates, and hence we can expect that a fundamental solution may be obtained among solutions that only depend upon the distance r from the source point. If we choose the volume to be a ball of radius a around the source point, then Gauss' divergence theorem implies that

It follows that
on a sphere of radius r that is centered around the source point, and hence
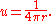
Note that, with the opposite sign convention (used in PhysicsPhysicsPhysics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
), this is the potentialPotential*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
generated by a point particlePoint particleA point particle is an idealization of particles heavily used in physics. Its defining feature is that it lacks spatial extension: being zero-dimensional, it does not take up space...
, for an inverse-square lawInverse-square lawIn physics, an inverse-square law is any physical law stating that a specified physical quantity or strength is inversely proportional to the square of the distance from the source of that physical quantity....
force, arising in the solution of Poisson equation.
A similar argument shows that in two dimensions
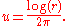
where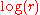 denotes the natural logarithmNatural logarithmThe natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
denotes the natural logarithmNatural logarithmThe natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
.
Note that, with the opposite sign convention, this is the potentialPotential*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
generated by a pointlike vortexVortexA vortex is a spinning, often turbulent,flow of fluid. Any spiral motion with closed streamlines is vortex flow. The motion of the fluid swirling rapidly around a center is called a vortex...
(see point particlePoint particleA point particle is an idealization of particles heavily used in physics. Its defining feature is that it lacks spatial extension: being zero-dimensional, it does not take up space...
), which is the solution of Euler equations in two-dimensional incompressible flowIncompressible flowIn fluid mechanics or more generally continuum mechanics, incompressible flow refers to flow in which the material density is constant within an infinitesimal volume that moves with the velocity of the fluid...
.
Green's function
A Green's functionGreen's functionIn mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
is a fundamental solution that also satisfies a suitable condition on the boundary S of a volume V. For instance,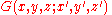 may satisfy
may satisfy
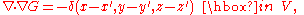
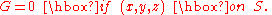
Now if u is any solution of the Poisson equation in V:

and u assumes the boundary values g on S, then we may apply Green's identityGreen's identitiesIn mathematics, Green's identities are a set of three identities in vector calculus. They are named after the mathematician George Green, who discovered Green's theorem.-Green's first identity:...
, (a consequence of the divergence theorem) which states that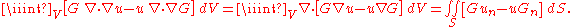
The notations un and Gn denote normal derivatives on S. In view of the conditions satisfied by u and G, this result simplifies to
Thus the Green's function describes the influence at of the data f and g. For the case of the interior of a sphere of radius a, the Green's function may be obtained by means of a reflection (Sommerfeld, 1949): the source point P at distance ρ from the center of the sphere is reflected along its radial line to a point P that is at a distance
of the data f and g. For the case of the interior of a sphere of radius a, the Green's function may be obtained by means of a reflection (Sommerfeld, 1949): the source point P at distance ρ from the center of the sphere is reflected along its radial line to a point P that is at a distance
Note that if P is inside the sphere, then P will be outside the sphere. The Green's function is then given by

where R denotes the distance to the source point P and R' denotes the distance to the reflected point P. A consequence of this expression for the Green's function is the Poisson integral formula. Let ρ, θ, and φ be spherical coordinates for the source point P. Here θ denotes the angle with the vertical axis, which is contrary to the usual American mathematical notation, but agrees with standard European and physical practice. Then the solution of the Laplace equation inside the sphere is given by
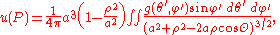
where

A simple consequence of this formula is that if u is a harmonic function, then the value of u at the center of the sphere is the mean value of its values on the sphere. This mean value property immediately implies that a non-constant harmonic function cannot assume its maximum value at an interior point.
Electrostatics
In free space the Laplace equation of any electrostatic potential must equal zero since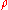 (charge density) is zero in free space.
(charge density) is zero in free space.
Taking the gradient of the electric potential we get the electrostatic field

Taking the divergence of the electrostatic field, we obtain Poisson's equation, that relates charge density and electric potential
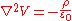
In the particular case of the empty space ( ) Poisson's equation reduces to Laplace's equation for the electric potential.
) Poisson's equation reduces to Laplace's equation for the electric potential.
Using a uniqueness theorem and showing that a potential satisfies Laplace's equation (second derivative of V should be zero i.e. in free space) and the potential has the correct values at the boundaries, the potential is then uniquely defined.
A potential that doesn't satisfy Laplace's equation together with the boundary condition is an invalid electrostatic potential.
See also
- Spherical harmonicSpherical HarmonicSpherical Harmonic is a science fiction novel from the Saga of the Skolian Empire by Catherine Asaro. It tells the story of Dyhianna Selei , the Ruby Pharaoh of the Skolian Imperialate, as she strives to reform her government and reunite her family in the aftermath of a devastating interstellar...
- Quadrature domainsQuadrature domainsIn the branch of mathematics called potential theory, a quadrature domain in two dimensional real Euclidean space is a domain D together with...
- Potential theoryPotential theoryIn mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
- Potential flowPotential flowIn fluid dynamics, potential flow describes the velocity field as the gradient of a scalar function: the velocity potential. As a result, a potential flow is characterized by an irrotational velocity field, which is a valid approximation for several applications...
- Bateman transformBateman transformIn the mathematical study of partial differential equation, the Bateman transform is a method for solving the Laplace equation in four dimensions and wave equation in three by using a line integral of a holomorphic function in three complex variables...
- Earnshaw's theoremEarnshaw's theoremEarnshaw's theorem states that a collection of point charges cannot be maintained in a stable stationary equilibrium configuration solely by the electrostatic interaction of the charges. This was first proven by British mathematician Samuel Earnshaw in 1842. It is usually referenced to magnetic...
uses the Laplace equation to show that stable static ferromagnetic suspension is impossible - Vector LaplacianVector LaplacianIn mathematics and physics, the vector Laplace operator, denoted by \scriptstyle \nabla^2, named after Pierre-Simon Laplace, is a differential operator defined over a vector field. The vector Laplacian is similar to the scalar Laplacian...
External links
- Laplace Equation (particular solutions and boundary value problems) at EqWorld: The World of Mathematical Equations.
- Laplace Differential Equation on PlanetMathPlanetMathPlanetMath is a free, collaborative, online mathematics encyclopedia. The emphasis is on rigour, openness, pedagogy, real-time content, interlinked content, and also community of about 24,000 people with various maths interests. Intended to be comprehensive, the project is hosted by the Digital...
- Example initial-boundary value problems using Laplace's equation from exampleproblems.com.
- Module for Laplace’s Equation by John H. Mathews
- Find out how boundary value problems governed by Laplace's equation may be solved numerically by boundary element method
-
-