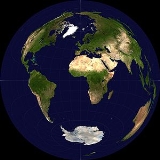
Lambert azimuthal equal-area projection
Encyclopedia
The Lambert azimuthal equal-area projection is a particular mapping from a sphere to a disk
(that is, a region bounded by a circle). It accurately represents area
in all regions of the sphere, but it does not accurately represent angle
s. It is named for the Swiss
mathematician Johann Heinrich Lambert
, who announced it in 1772.
The Lambert azimuthal projection is used as a map projection
in cartography
. For example, the National Atlas of the US
uses a Lambert azimuthal equal-area projection to display information in the online Map Maker application, and the European Environment Agency
recommends its usage for European mapping for statistical analysis and display. It is also used in scientific disciplines such as geology
for plotting the orientations of lines in three-dimensional space. This plotting is aided by a special kind of graph paper
called a Schmidt net.
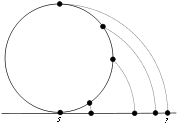 To define the Lambert azimuthal projection, imagine a plane set tangent to the sphere at some point S on the sphere. Let P be any point on the sphere other than the antipode
To define the Lambert azimuthal projection, imagine a plane set tangent to the sphere at some point S on the sphere. Let P be any point on the sphere other than the antipode
of S. Let d be the distance between S and P in three-dimensional space (not the distance along the sphere surface). Then the projection sends P to a point P′ on the plane that is a distance d from S.
To make this more precise, there is a unique circle centered at S, passing through P, and perpendicular to the plane. It intersects the plane in two points; let P' be the one that is closer to P. This is the projected point. See the figure. The antipode of S is excluded from the projection because the required circle is not unique. The case of S is degenerate; S is projected to itself, along a circle of radius 0.
Explicit formulas are required for carrying out the projection on a computer
. Consider the projection centered at S = (0, 0, -1) on the unit sphere
, which is the set of points (x, y, z) in three-dimensional space such that x2 + y2 + z2 = 1. In Cartesian coordinates
such that x2 + y2 + z2 = 1. In Cartesian coordinates  on the sphere and
on the sphere and 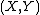 on the plane, the projection and its inverse are then described by
on the plane, the projection and its inverse are then described by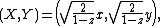
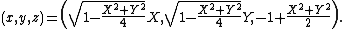
In spherical coordinates on the sphere (with
on the sphere (with  the zenith and
the zenith and  the azimuth) and polar coordinates
the azimuth) and polar coordinates  on the disk, the map and its inverse are given by
on the disk, the map and its inverse are given by 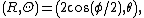
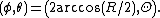
In cylindrical coordinates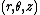 on the sphere and polar coordinates
on the sphere and polar coordinates 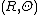 on the plane, the map and its inverse are given by
on the plane, the map and its inverse are given by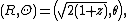

The projection can be centered at other points, and defined on spheres of radius other than 1, using similar formulas.
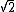 centered at (0, 0), and the lower hemisphere
centered at (0, 0), and the lower hemisphere  to the open disk contained in that circle.
to the open disk contained in that circle.
The projection is a diffeomorphism
(a bijection
that is infinitely differentiable in both directions) between the sphere (minus (0, 0, 1)) and the open disk of radius 2. It is an area-preserving (equal-area) map, which can be seen by computing the area element
of the sphere when parametrized by the inverse of the projection. In Cartesian coordinates it is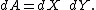
This means that measuring the area of a region on the sphere is tantamount to measuring the area of the corresponding region the disk.
On the other hand, the projection does not preserve angular relationships among curves on the sphere. No mapping between a portion of a sphere and the plane can preserve both angles and areas. (If one did, then it would be a local isometry
and would preserve Gaussian curvature
; but the sphere and disk have different curvatures, so this is impossible.) This fact, that flat pictures cannot perfectly represent regions of spheres, is the fundamental problem of cartography.
As a consequence, regions on the sphere may be projected to the plane with greatly distorted shapes. This distortion is particularly dramatic far away from the center of the projection (0, 0, -1). In practice the projection is often restricted to the hemisphere centered at that point; the other hemisphere can be mapped separately, using a second projection centered at the antipode.
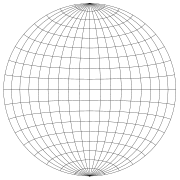 The Lambert azimuthal projection can be carried out by a computer using the explicit formulas given above. However, for graphing by hand these formulas are unwieldy; instead, it is common to use graph paper, called a Schmidt net, designed specifically for the task. To make this graph paper, one places a grid of parallels
The Lambert azimuthal projection can be carried out by a computer using the explicit formulas given above. However, for graphing by hand these formulas are unwieldy; instead, it is common to use graph paper, called a Schmidt net, designed specifically for the task. To make this graph paper, one places a grid of parallels
and meridians on the hemisphere, and then projects these curves to the disk.
In the figure, the area-preserving property of the projection can be seen by comparing a grid sector near the center of the net with one at the far right of the net. The two sectors have the same area on the sphere and the same area on the disk. The angle-distorting property can be seen by examining the grid lines; most of them do not intersect at right angles on the Schmidt net.
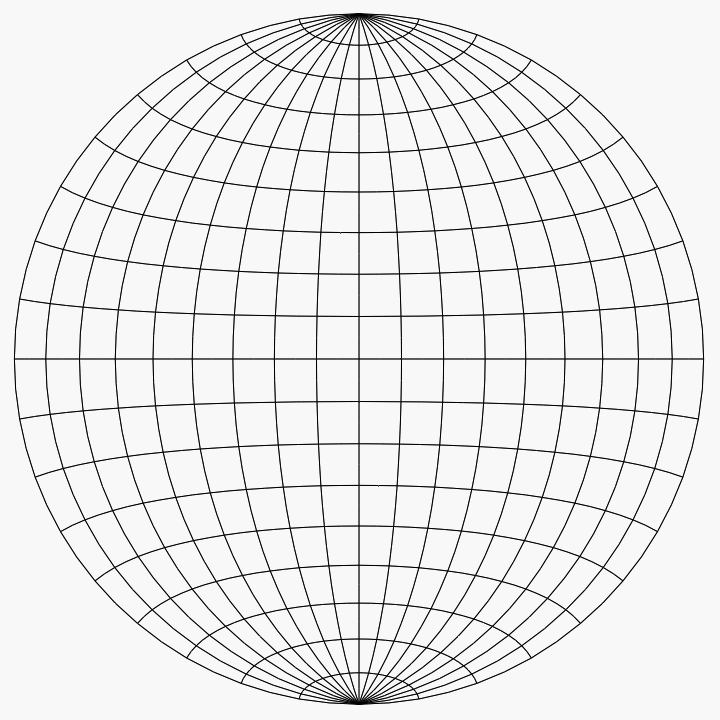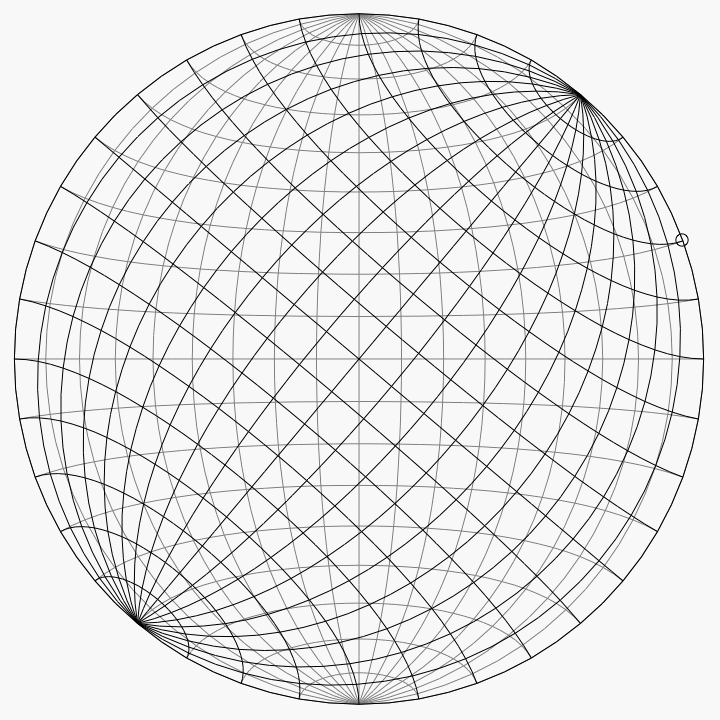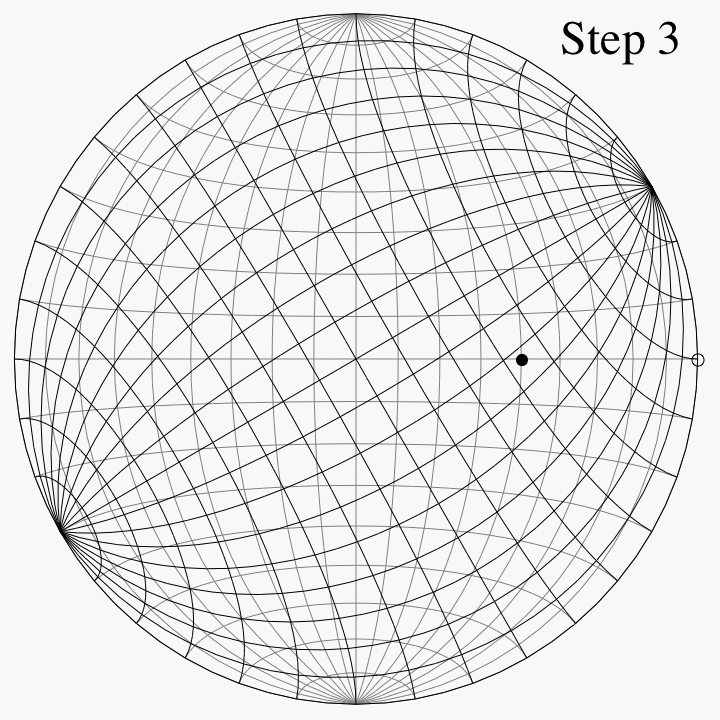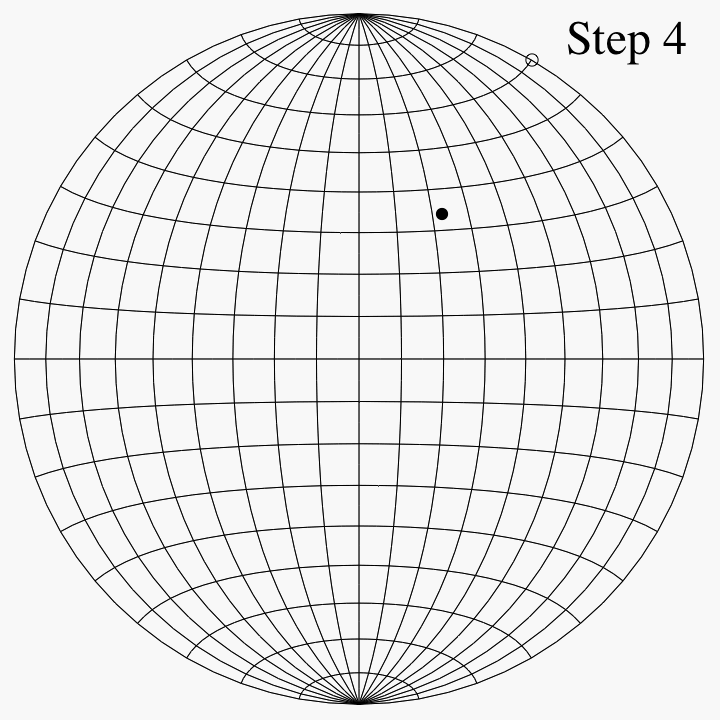 For an example of the use of the Schmidt net, imagine that we have two copies of it on thin paper, one atop the other, aligned and tacked at their mutual center. Suppose that we want to plot the point (0.321, 0.557, -0.766) on the lower unit hemisphere. This point lies on a line oriented 60° counterclockwise from the positive x-axis (or 30° clockwise from the positive y-axis) and 50° below the horizontal plane z = 0. Once these angles are known, there are four steps:
For an example of the use of the Schmidt net, imagine that we have two copies of it on thin paper, one atop the other, aligned and tacked at their mutual center. Suppose that we want to plot the point (0.321, 0.557, -0.766) on the lower unit hemisphere. This point lies on a line oriented 60° counterclockwise from the positive x-axis (or 30° clockwise from the positive y-axis) and 50° below the horizontal plane z = 0. Once these angles are known, there are four steps:
To plot other points, whose angles are not such round numbers as 60° and 50°, one must visually interpolate between the nearest grid lines. It is helpful to have a net with finer spacing than 10°; spacings of 2° are common.
to plot directional data, as follows.
A direction in three-dimensional space corresponds to a line through the origin. The set of all such lines is itself a space, called the real projective plane
in mathematics
. Every line through the origin intersects the unit sphere in exactly two points, one of which is on the lower hemisphere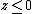 . (Horizontal lines intersect the equator
. (Horizontal lines intersect the equator 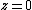 in two antipodal points. It is understood that antipodal points on the equator represent a single line. See quotient topology.) Hence the directions in three-dimensional space correspond (almost perfectly) to points on the lower hemisphere. The hemisphere can then be plotted as a disk of radius
in two antipodal points. It is understood that antipodal points on the equator represent a single line. See quotient topology.) Hence the directions in three-dimensional space correspond (almost perfectly) to points on the lower hemisphere. The hemisphere can then be plotted as a disk of radius  using the Lambert azimuthal projection.
using the Lambert azimuthal projection.
Thus the Lambert azimuthal projection lets us plot directions as points in a disk. Due to the equal-area property of the projection, one can integrate
over regions of the real projective plane (the space of directions) by integrating over the corresponding regions on the disk. This is useful for statistical analysis of directional data.
Not only lines but also planes through the origin can be plotted with the Lambert azimuthal projection. A plane intersects the hemisphere in a circular arc, called the trace of the plane, which projects down to a curve (typically non-circular) in the disk. One can plot this curve, or one can alternatively replace the plane with the line perpendicular to it, called the pole, and plot that line instead. When many planes are being plotted together, plotting poles instead of traces produces a less cluttered plot.
Researchers in structural geology
use the Lambert azimuthal projection to plot crystallographic
axes and faces, lineation and foliation
in rocks, slickenside
s in faults, and other linear and planar features. In this context the projection is called the equal-area hemispherical projection. There is also an equal-angle hemispherical projection defined by stereographic projection
.
The discussion here has emphasized the lower hemisphere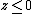 , but some disciplines prefer the upper hemisphere
, but some disciplines prefer the upper hemisphere 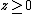 . Indeed, any hemisphere can be used to record the lines through the origin in three-dimensional space.
. Indeed, any hemisphere can be used to record the lines through the origin in three-dimensional space.
Disk (mathematics)
In geometry, a disk is the region in a plane bounded by a circle.A disk is said to be closed or open according to whether or not it contains the circle that constitutes its boundary...
(that is, a region bounded by a circle). It accurately represents area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
in all regions of the sphere, but it does not accurately represent angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
s. It is named for the Swiss
Switzerland
Switzerland name of one of the Swiss cantons. ; ; ; or ), in its full name the Swiss Confederation , is a federal republic consisting of 26 cantons, with Bern as the seat of the federal authorities. The country is situated in Western Europe,Or Central Europe depending on the definition....
mathematician Johann Heinrich Lambert
Johann Heinrich Lambert
Johann Heinrich Lambert was a Swiss mathematician, physicist, philosopher and astronomer.Asteroid 187 Lamberta was named in his honour.-Biography:...
, who announced it in 1772.
The Lambert azimuthal projection is used as a map projection
Map projection
A map projection is any method of representing the surface of a sphere or other three-dimensional body on a plane. Map projections are necessary for creating maps. All map projections distort the surface in some fashion...
in cartography
Cartography
Cartography is the study and practice of making maps. Combining science, aesthetics, and technique, cartography builds on the premise that reality can be modeled in ways that communicate spatial information effectively.The fundamental problems of traditional cartography are to:*Set the map's...
. For example, the National Atlas of the US
National Atlas of the United States
The National Atlas of the United States is an online atlas published by the United States Department of the Interior.Since it is a publication of the United States Government, the atlas and the maps contained therein are in the public domain....
uses a Lambert azimuthal equal-area projection to display information in the online Map Maker application, and the European Environment Agency
European Environment Agency
European Environment Agency is an agency of the European Union. Its task is to provide sound, independent information on the environment. It is a major information source for those involved in developing, adopting, implementing and evaluating environmental policy, and also the general public...
recommends its usage for European mapping for statistical analysis and display. It is also used in scientific disciplines such as geology
Geology
Geology is the science comprising the study of solid Earth, the rocks of which it is composed, and the processes by which it evolves. Geology gives insight into the history of the Earth, as it provides the primary evidence for plate tectonics, the evolutionary history of life, and past climates...
for plotting the orientations of lines in three-dimensional space. This plotting is aided by a special kind of graph paper
Graph paper
Graph paper, graphing paper, grid paper or millimeter paper is writing paper that is printed with fine lines making up a regular grid. The lines are often used as guides for plotting mathematical functions or experimental data and drawing diagrams. It is commonly found in mathematics and...
called a Schmidt net.
Definition

Antipode
Antipode, Antipodes, or Antipodeans may refer to:* Antipodal point, the diametrically opposite point on a sphere* Antipodes Water Company, a premium bottled water brand...
of S. Let d be the distance between S and P in three-dimensional space (not the distance along the sphere surface). Then the projection sends P to a point P′ on the plane that is a distance d from S.
To make this more precise, there is a unique circle centered at S, passing through P, and perpendicular to the plane. It intersects the plane in two points; let P
Explicit formulas are required for carrying out the projection on a computer
Computer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
. Consider the projection centered at S = (0, 0, -1) on the unit sphere
Unit sphere
In mathematics, a unit sphere is the set of points of distance 1 from a fixed central point, where a generalized concept of distance may be used; a closed unit ball is the set of points of distance less than or equal to 1 from a fixed central point...
, which is the set of points (x, y, z) in three-dimensional space
 such that x2 + y2 + z2 = 1. In Cartesian coordinates
such that x2 + y2 + z2 = 1. In Cartesian coordinates  on the sphere and
on the sphere and 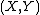 on the plane, the projection and its inverse are then described by
on the plane, the projection and its inverse are then described by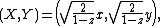
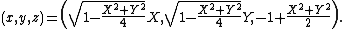
In spherical coordinates
 on the sphere (with
on the sphere (with 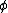 the zenith and
the zenith and 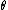 the azimuth) and polar coordinates
the azimuth) and polar coordinates 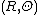 on the disk, the map and its inverse are given by
on the disk, the map and its inverse are given by 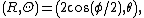
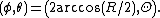
In cylindrical coordinates
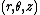 on the sphere and polar coordinates
on the sphere and polar coordinates 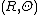 on the plane, the map and its inverse are given by
on the plane, the map and its inverse are given by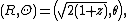

The projection can be centered at other points, and defined on spheres of radius other than 1, using similar formulas.
Properties
As defined in the preceding section, the Lambert azimuthal projection of the unit sphere is undefined at (0, 0, 1). It sends the rest of the sphere to the open disk of radius 2 centered at the origin (0, 0) in the plane. It sends the point (0, 0, -1) to (0, 0), the equator z = 0 to the circle of radius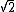 centered at (0, 0), and the lower hemisphere
centered at (0, 0), and the lower hemisphere 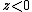 to the open disk contained in that circle.
to the open disk contained in that circle.The projection is a diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
(a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
that is infinitely differentiable in both directions) between the sphere (minus (0, 0, 1)) and the open disk of radius 2. It is an area-preserving (equal-area) map, which can be seen by computing the area element
Surface integral
In mathematics, a surface integral is a definite integral taken over a surface ; it can be thought of as the double integral analog of the line integral...
of the sphere when parametrized by the inverse of the projection. In Cartesian coordinates it is
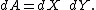
This means that measuring the area of a region on the sphere is tantamount to measuring the area of the corresponding region the disk.
On the other hand, the projection does not preserve angular relationships among curves on the sphere. No mapping between a portion of a sphere and the plane can preserve both angles and areas. (If one did, then it would be a local isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
and would preserve Gaussian curvature
Gaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
; but the sphere and disk have different curvatures, so this is impossible.) This fact, that flat pictures cannot perfectly represent regions of spheres, is the fundamental problem of cartography.
As a consequence, regions on the sphere may be projected to the plane with greatly distorted shapes. This distortion is particularly dramatic far away from the center of the projection (0, 0, -1). In practice the projection is often restricted to the hemisphere centered at that point; the other hemisphere can be mapped separately, using a second projection centered at the antipode.
Schmidt net

Circle of latitude
A circle of latitude, on the Earth, is an imaginary east-west circle connecting all locations that share a given latitude...
and meridians on the hemisphere, and then projects these curves to the disk.
In the figure, the area-preserving property of the projection can be seen by comparing a grid sector near the center of the net with one at the far right of the net. The two sectors have the same area on the sphere and the same area on the disk. The angle-distorting property can be seen by examining the grid lines; most of them do not intersect at right angles on the Schmidt net.

- Using the grid lines, which are spaced 10° apart in the figures here, mark the point on the edge of the net that is 60° counterclockwise from the point (1, 0) (or 30° clockwise from the point (0, 1)).
- Rotate the top net until this point is aligned with (1, 0) on the bottom net.
- Using the grid lines on the bottom net, mark the point that is 50° toward the center from that point.
- Rotate the top net oppositely to how it was rotated before, to bring it back into alignment with the bottom net. The point just marked is then the projection that we wanted.
To plot other points, whose angles are not such round numbers as 60° and 50°, one must visually interpolate between the nearest grid lines. It is helpful to have a net with finer spacing than 10°; spacings of 2° are common.
Applications
The Lambert azimuthal projection was originally conceived as an equal-area map projection. It is now also used in disciplines such as geologyGeology
Geology is the science comprising the study of solid Earth, the rocks of which it is composed, and the processes by which it evolves. Geology gives insight into the history of the Earth, as it provides the primary evidence for plate tectonics, the evolutionary history of life, and past climates...
to plot directional data, as follows.
A direction in three-dimensional space corresponds to a line through the origin. The set of all such lines is itself a space, called the real projective plane
Real projective plane
In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
. Every line through the origin intersects the unit sphere in exactly two points, one of which is on the lower hemisphere
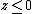 . (Horizontal lines intersect the equator
. (Horizontal lines intersect the equator 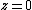 in two antipodal points. It is understood that antipodal points on the equator represent a single line. See quotient topology.) Hence the directions in three-dimensional space correspond (almost perfectly) to points on the lower hemisphere. The hemisphere can then be plotted as a disk of radius
in two antipodal points. It is understood that antipodal points on the equator represent a single line. See quotient topology.) Hence the directions in three-dimensional space correspond (almost perfectly) to points on the lower hemisphere. The hemisphere can then be plotted as a disk of radius  using the Lambert azimuthal projection.
using the Lambert azimuthal projection.Thus the Lambert azimuthal projection lets us plot directions as points in a disk. Due to the equal-area property of the projection, one can integrate
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
over regions of the real projective plane (the space of directions) by integrating over the corresponding regions on the disk. This is useful for statistical analysis of directional data.
Not only lines but also planes through the origin can be plotted with the Lambert azimuthal projection. A plane intersects the hemisphere in a circular arc, called the trace of the plane, which projects down to a curve (typically non-circular) in the disk. One can plot this curve, or one can alternatively replace the plane with the line perpendicular to it, called the pole, and plot that line instead. When many planes are being plotted together, plotting poles instead of traces produces a less cluttered plot.
Researchers in structural geology
Structural geology
Structural geology is the study of the three-dimensional distribution of rock units with respect to their deformational histories. The primary goal of structural geology is to use measurements of present-day rock geometries to uncover information about the history of deformation in the rocks, and...
use the Lambert azimuthal projection to plot crystallographic
Crystallography
Crystallography is the experimental science of the arrangement of atoms in solids. The word "crystallography" derives from the Greek words crystallon = cold drop / frozen drop, with its meaning extending to all solids with some degree of transparency, and grapho = write.Before the development of...
axes and faces, lineation and foliation
Foliation (geology)
Foliation is any penetrative planar fabric present in rocks. Foliation is common to rocks affected by regional metamorphic compression typical of orogenic belts. Rocks exhibiting foliation include the standard sequence formed by the prograde metamorphism of mudrocks; slate, phyllite, schist and...
in rocks, slickenside
Slickenside
thumb|Slickensides on a sample of sandstone of the [[Juniata Formation]], from an outcrop on [[U.S. Route 322|Rt 322]] northeast of State College, Pennsylvania250px|thumb|left|How slickenfibre steps form and show sense of movement on a fault...
s in faults, and other linear and planar features. In this context the projection is called the equal-area hemispherical projection. There is also an equal-angle hemispherical projection defined by stereographic projection
Stereographic projection
The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
.
The discussion here has emphasized the lower hemisphere
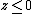 , but some disciplines prefer the upper hemisphere
, but some disciplines prefer the upper hemisphere 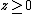 . Indeed, any hemisphere can be used to record the lines through the origin in three-dimensional space.
. Indeed, any hemisphere can be used to record the lines through the origin in three-dimensional space.

