Kirillov orbit theory
Encyclopedia
In mathematics
, the orbit method (also known as the Kirillov theory, the method of coadjoint orbits and by a few similar names) establishes a correspondence between irreducible unitary representation
s of a Lie group
and its coadjoint orbits: orbits of the action of the group
on the dual space of its Lie algebra
. The theory was introduced by for nilpotent group
s and later extended by Bertram Kostant
, Louis Auslander
, Lajos Pukánszky
and others to the case of solvable group
s. Roger Howe
found a version of the orbit method that applies to p-adic Lie groups. David Vogan
proposed that the orbit method should serve as a unifying principle in the description of the unitary duals of real reductive Lie groups.
s whose symplectic structure is invariant under G. If an orbit is the phase space
of a G-invariant classical mechanical system
then the corresponding quantum mechanical system ought to be described via an irreducible unitary representation of G. Geometric invariants of the orbit translate into algebraic invariants of the corresponding representation. In this way the orbit method may be viewed as a precise mathematical manifestation of a vague physical principle of quantization. In the case of a nilpotent group G the correspondence involves all orbits, but for a general G additional restrictions on the orbit are necessary (polarizability, integrality, Pukanszky condition). This point of view has been significantly advanced by Kostant in his theory of geometric quantization
of coadjoint orbits.
, simply connected nilpotent
Lie group
. Kirillov proved that the equivalence classes of irreducible unitary representation
s of G are parametrized by the coadjoint orbits of G, that is the orbits of the action G on the dual space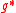
of its Lie algebra. The Kirillov character formula
expresses the Harish-Chandra character
of the representation as a certain integral over the corresponding orbit.
and each of them intersects the positive Weyl chamber h*+ in a single point. An orbit is integral if this point belongs to the weight lattice of G.
The highest weight theory can be restated in the form of a bijection between the set of integral coadjoint orbits and the set of equivalence classes of irreducible unitary representations of G: the highest weight representation L(λ) with highest weight λ∈h*+ corresponds to the integral coadjoint orbit G·λ. The Kirillov character formula amounts to the character formula earlier proved by Harish-Chandra
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the orbit method (also known as the Kirillov theory, the method of coadjoint orbits and by a few similar names) establishes a correspondence between irreducible unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
s of a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
and its coadjoint orbits: orbits of the action of the group
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on the dual space of its Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
. The theory was introduced by for nilpotent group
Nilpotent group
In mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
s and later extended by Bertram Kostant
Bertram Kostant
-Early life and education:Kostant grew up in New York City, where he graduated from the celebrated Stuyvesant High School in 1945. He went on to obtain an undergraduate degree in mathematics from Purdue University in 1950. He earned his Ph.D...
, Louis Auslander
Louis Auslander
Louis Auslander was an American mathematician. He had wide ranging interests both in pure and applied mathematics and worked on Finsler geometry, geometry of solvmanifolds and nilmanifolds, locally affine spaces, many aspects of harmonic analysis, representation theory of solvable Lie groups, and...
, Lajos Pukánszky
Lajos Pukánszky
Lajos Pukánszky was a Hungarian and American mathematician noted for his work in representation theory of solvable Lie groups. He was born in Budapest on November 24, 1928, defended his thesis in 1955 at the University of Szeged under Béla Szőkefalvi-Nagy, but left Hungary in 1956...
and others to the case of solvable group
Solvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
s. Roger Howe
Roger Evans Howe
Roger Evans Howe is the William R. Kenan Jr. Professor of Mathematics at Yale University. He is well known for his contributions to representation theory, and in particular for the notion of a reductive dual pair, sometimes known as a Howe pair, and the Howe correspondence.He attended Ithaca High...
found a version of the orbit method that applies to p-adic Lie groups. David Vogan
David Vogan
David Alexander Vogan is a mathematician at M.I.T. who works on unitary representations of simple Lie groups. He is one of the participants in the Atlas of Lie Groups and Representations.-Publications:*Some online by Vogan...
proposed that the orbit method should serve as a unifying principle in the description of the unitary duals of real reductive Lie groups.
Relation with symplectic geometry
One of the key observations of Kirillov was that coadjoint orbits of a Lie group G have natural structure of symplectic manifoldSymplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
s whose symplectic structure is invariant under G. If an orbit is the phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
of a G-invariant classical mechanical system
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
then the corresponding quantum mechanical system ought to be described via an irreducible unitary representation of G. Geometric invariants of the orbit translate into algebraic invariants of the corresponding representation. In this way the orbit method may be viewed as a precise mathematical manifestation of a vague physical principle of quantization. In the case of a nilpotent group G the correspondence involves all orbits, but for a general G additional restrictions on the orbit are necessary (polarizability, integrality, Pukanszky condition). This point of view has been significantly advanced by Kostant in his theory of geometric quantization
Geometric quantization
In mathematical physics, geometric quantization is a mathematical approach to defining a quantum theory corresponding to a given classical theory. It attempts to carry out quantization, for which there is in general no exact recipe, in such a way that certain analogies between the classical theory...
of coadjoint orbits.
Nilpotent group case
Let G be a connectedConnected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
, simply connected nilpotent
Nilpotent group
In mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
. Kirillov proved that the equivalence classes of irreducible unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
s of G are parametrized by the coadjoint orbits of G, that is the orbits of the action G on the dual space
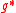of its Lie algebra. The Kirillov character formulaKirillov character formula
In mathematics, for a Lie group G, the Kirillov orbit method gives a heuristic method in representation theory. It connects the Fourier transforms of coadjoint orbits, which lie in the dual space of the Lie algebra of G, to the infinitesimal characters of the irreducible representations...
expresses the Harish-Chandra character
Harish-Chandra character
In mathematics, the Harish-Chandra character, named after Harish-Chandra, of a representation of a semisimple Lie group G on a Hilbert space H is a distribution on the group G that is analogous to the character of a finite dimensional representation of a compact group.-Definition:Suppose that π...
of the representation as a certain integral over the corresponding orbit.
Compact Lie group case
Complex irreducible representations of compact Lie groups have been completely classified. They are always finite-dimensional, unitarizable (i.e. admit an invariant positive definite Hermitian form) and are parametrized by their highest weights, which are precisely the dominant integral weights for the group. If G is a compact semisimple Lie group with a Cartan subalgebra h then its coadjoint orbits are closedClosed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
and each of them intersects the positive Weyl chamber h*+ in a single point. An orbit is integral if this point belongs to the weight lattice of G.
The highest weight theory can be restated in the form of a bijection between the set of integral coadjoint orbits and the set of equivalence classes of irreducible unitary representations of G: the highest weight representation L(λ) with highest weight λ∈h*+ corresponds to the integral coadjoint orbit G·λ. The Kirillov character formula amounts to the character formula earlier proved by Harish-Chandra
Harish-Chandra
Harish-Chandra was an Indian mathematician, who did fundamental work in representation theory, especially Harmonic analysis on semisimple Lie groups. -Life:...
.