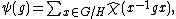Induced representation
Encyclopedia
In mathematics
, and in particular group representation
theory, the induced representation is one of the major general operations for passing from a representation of a subgroup
H to a representation of the (whole) group
G itself. It was initially defined as a construction by Frobenius
, for linear representations of finite group
s. It includes as special cases the action of G on the cosets G/H by permutation, which is the case of the induced representation starting with the trivial one-dimensional representation of H. If H = {e} this becomes the regular representation
of G. Therefore induced representations are rich objects, in the sense that they include or detect many interesting representations. The idea is by no means limited to the case of finite groups, but the theory in that case is particularly well-behaved.
): any linear representation of G, as K[G]-module
where K[G] is the group ring
of G over a field K, is also a K[H]-module. The theorem states that, given representations ρ of G and σ of H, the space of G-equivariant
linear maps from ρ to Ind(σ) has the same dimension as that of the H-equivariant linear maps from Res(ρ) to σ. (Here Res stands for restricted representation
, and Ind for induced representation.) It is useful (in the typical case of non-modular representations, anyway - say with K = C) for computing the decomposition of the induced representation: we can do calculations on the side of H, which is the 'small' group.
The Frobenius formula states that if χ is the character of the representation σ, given by χ(h) = Tr σ(h), then the character ψ of the induced representation is given by
where is defined to be χ on H and 0 off H.
is defined to be χ on H and 0 off H.
Frobenius reciprocity shows that Res and Ind are adjoint functors. More precisely, Ind is the left adjoint to Res. But in the finite group case, it is also a right adjoint, so (Res, Ind) is a Frobenius pair. The content of that statement is more than the dimensions: it requires that the isomorphism of vector spaces of intertwining maps be natural, in the sense of category theory
. It actually suggests that induced representation can in this case be defined by means of the adjunction. That's not the only way to do it - and perhaps not the only helpful way - but it means that the theory will not be ad hoc
in its start.
One can therefore make the reciprocity theorem the way to define the induced representation. There is another way, suggested by the permutation examples of the introductory paragraph. The induced representation Ind(σ) should be realized as a space of functions on G transforming under H according to the representation σ. Therefore if σ acts on the vector space
V, we should look at V-valued functions on G on which H acts via σ (this must be said carefully with explicit talk about left- and right-actions). This approach allows the induced representation to be a kind of free module
construction.
The two approaches outlined above can be reconciled in the case of finite groups, by using the tensor product
with K[G] as a K[H]-module. There is a third and classical approach, of simply writing down the character (trace) of the induced representation, in terms of conjugation in G of elements g into H.
The reciprocity formula can sometimes be generalized to more general topological groups; for example, the Selberg trace formula
and the Arthur-Selberg trace formula are generalizations of Frobenius reciprocity to discrete cofinite subgroups of certain locally compact groups.
 can be thought of as acting on the following space:
can be thought of as acting on the following space: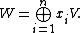
Here each xi V is an isomorphic copy of the vector space V.
For each g in G and each xi there is an h = hi in H and j = j(i) in { 1, …, n } such that gxi = xjh. This is just another way of saying that x1, …, xn is a full set of representatives. Via the induced representation G acts on W as follows: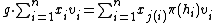
where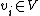 for each
for each  .
.
As mentioned earlier this construction is equivalent to defining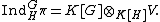
(possibly infinite) and H is a closed
subgroup
then there is a common analytic construction of the induced representation. Let (π,V) be a continuous
representation of H into a Hilbert space
V. We can then let: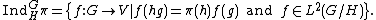
Here L2(G) is taken with respect to a Haar measure
. The group G acts on the induced representation space by right translation, that is, (g·f)(x) = f(xg).
This construction is often modified in various ways to fit the applications needed. A common version is called normalized induction and usually uses the same notation. The definition of the representation space is as follows: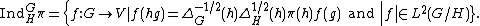
Here ΔG and ΔH are the modular functions
of G and H respectively. With the addition of the normalizing factors this induction functor
takes unitary representation
s to unitary representations.
One other variation on induction is called compact induction. This is just standard induction restricted to functions with compact support. Formally it is denoted by ind and defined as: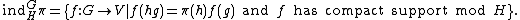
Note that if G/H is compact then Ind and ind are the same functor.
and H is a closed
subgroup
of G. Also, suppose σ is a realization of H over the space V. The product V×G is a realization of G as follows:
where g and g′ are elements of G and x is an element of V.
Define the equivalence relation
~(h[x],hg).
Note that this equivalence relation is invariant under the action of G. In other words, V×G/~ is a realization of G.
In other words, V×G/~ is a fiber bundle
over the quotient space
G/H with H as the structure group and V as the fiber.
Now suppose σ is a representation and V is a vector space. The previous construction defines a vector bundle over G/H. The space of sections of this vector bundle is the induced representation.
In the case of unitary representation
s of locally compact groups, the induction construction can be formulated in terms of systems of imprimitivity
.
of the trivial subgroup is the right regular representation
. More generally the induced representation of the trivial representation
of any subgroup is the permutation representation on the cosets of that subgroup.
An induced representation of a one dimensional representation is called a monomial representation, because it can be represented as monomial matrices. Some groups have the property that all of their irreducible representations are monomial, the so-called monomial group
s.
In Lie theory, an extremely important example is parabolic induction
: inducing representations of a reductive group
from representations of its parabolic subgroups. This leads, via the philosophy of cusp forms, to the Langlands program
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and in particular group representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
theory, the induced representation is one of the major general operations for passing from a representation of a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
H to a representation of the (whole) group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G itself. It was initially defined as a construction by Frobenius
Ferdinand Georg Frobenius
Ferdinand Georg Frobenius was a German mathematician, best known for his contributions to the theory of differential equations and to group theory...
, for linear representations of finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s. It includes as special cases the action of G on the cosets G/H by permutation, which is the case of the induced representation starting with the trivial one-dimensional representation of H. If H = {e} this becomes the regular representation
Regular representation
In mathematics, and in particular the theory of group representations, the regular representation of a group G is the linear representation afforded by the group action of G on itself by translation....
of G. Therefore induced representations are rich objects, in the sense that they include or detect many interesting representations. The idea is by no means limited to the case of finite groups, but the theory in that case is particularly well-behaved.
Alternate formulations
The central theorem in the finite group case is the Frobenius reciprocity theorem. It is stated in terms of another construction of representations, the restriction map (which is a functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
): any linear representation of G, as K[G]-module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
where K[G] is the group ring
Group ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
of G over a field K, is also a K[H]-module. The theorem states that, given representations ρ of G and σ of H, the space of G-equivariant
Equivariant
In mathematics, an equivariant map is a function between two sets that commutes with the action of a group. Specifically, let G be a group and let X and Y be two associated G-sets. A function f : X → Y is said to be equivariant iffor all g ∈ G and all x in X...
linear maps from ρ to Ind(σ) has the same dimension as that of the H-equivariant linear maps from Res(ρ) to σ. (Here Res stands for restricted representation
Restricted representation
In mathematics, restriction is a fundamental construction in representation theory of groups. Restriction forms a representation of a subgroup from a representation of the whole group. Often the restricted representation is simpler to understand...
, and Ind for induced representation.) It is useful (in the typical case of non-modular representations, anyway - say with K = C) for computing the decomposition of the induced representation: we can do calculations on the side of H, which is the 'small' group.
The Frobenius formula states that if χ is the character of the representation σ, given by χ(h) = Tr σ(h), then the character ψ of the induced representation is given by
where
 is defined to be χ on H and 0 off H.
is defined to be χ on H and 0 off H.Frobenius reciprocity shows that Res and Ind are adjoint functors. More precisely, Ind is the left adjoint to Res. But in the finite group case, it is also a right adjoint, so (Res, Ind) is a Frobenius pair. The content of that statement is more than the dimensions: it requires that the isomorphism of vector spaces of intertwining maps be natural, in the sense of category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
. It actually suggests that induced representation can in this case be defined by means of the adjunction. That's not the only way to do it - and perhaps not the only helpful way - but it means that the theory will not be ad hoc
Ad hoc
Ad hoc is a Latin phrase meaning "for this". It generally signifies a solution designed for a specific problem or task, non-generalizable, and not intended to be able to be adapted to other purposes. Compare A priori....
in its start.
One can therefore make the reciprocity theorem the way to define the induced representation. There is another way, suggested by the permutation examples of the introductory paragraph. The induced representation Ind(σ) should be realized as a space of functions on G transforming under H according to the representation σ. Therefore if σ acts on the vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V, we should look at V-valued functions on G on which H acts via σ (this must be said carefully with explicit talk about left- and right-actions). This approach allows the induced representation to be a kind of free module
Free module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
construction.
The two approaches outlined above can be reconciled in the case of finite groups, by using the tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
with K[G] as a K[H]-module. There is a third and classical approach, of simply writing down the character (trace) of the induced representation, in terms of conjugation in G of elements g into H.
The reciprocity formula can sometimes be generalized to more general topological groups; for example, the Selberg trace formula
Selberg trace formula
In mathematics, the Selberg trace formula, introduced by , is an expression for the character of the unitary representation of G on the space L2 of square-integrable functions, where G is a Lie group and Γ a cofinite discrete group...
and the Arthur-Selberg trace formula are generalizations of Frobenius reciprocity to discrete cofinite subgroups of certain locally compact groups.
Algebraic
Let G be a finite group and H any subgroup of G. Furthermore let (π,V) be a representation of H. Let n = [G:H] and let x1, …, xn be a full set of representatives in G of the cosets in G/H. The induced representation can be thought of as acting on the following space:
can be thought of as acting on the following space: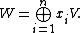
Here each xi V is an isomorphic copy of the vector space V.
For each g in G and each xi there is an h = hi in H and j = j(i) in { 1, …, n } such that gxi = xjh. This is just another way of saying that x1, …, xn is a full set of representatives. Via the induced representation G acts on W as follows:
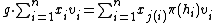
where
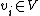 for each
for each  .
.As mentioned earlier this construction is equivalent to defining
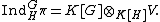
Analytic
If G is a locally compact topological groupTopological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
(possibly infinite) and H is a closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
then there is a common analytic construction of the induced representation. Let (π,V) be a continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
representation of H into a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
V. We can then let:
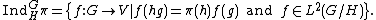
Here L2(G) is taken with respect to a Haar measure
Haar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
. The group G acts on the induced representation space by right translation, that is, (g·f)(x) = f(xg).
This construction is often modified in various ways to fit the applications needed. A common version is called normalized induction and usually uses the same notation. The definition of the representation space is as follows:
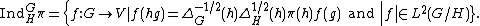
Here ΔG and ΔH are the modular functions
Haar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
of G and H respectively. With the addition of the normalizing factors this induction functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
takes unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
s to unitary representations.
One other variation on induction is called compact induction. This is just standard induction restricted to functions with compact support. Formally it is denoted by ind and defined as:
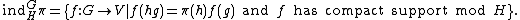
Note that if G/H is compact then Ind and ind are the same functor.
Geometric
Suppose G is a topological groupTopological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
and H is a closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of G. Also, suppose σ is a realization of H over the space V. The product V×G is a realization of G as follows:
- g′[(x,g)]=(x,gg′−1)
where g and g′ are elements of G and x is an element of V.
Define the equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
~(h[x],hg).
Note that this equivalence relation is invariant under the action of G. In other words, V×G/~ is a realization of G.
- g−1hg[(x,g)]=(x,h−1g)~(h[x],g)
In other words, V×G/~ is a fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
over the quotient space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
G/H with H as the structure group and V as the fiber.
Now suppose σ is a representation and V is a vector space. The previous construction defines a vector bundle over G/H. The space of sections of this vector bundle is the induced representation.
In the case of unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
s of locally compact groups, the induction construction can be formulated in terms of systems of imprimitivity
System of imprimitivity
The concept of system of imprimitivity is used in mathematics, particularly in algebra and analysis, both within the context of the theory of group representations...
.
Examples
For any group, the induced representation of the trivial representationTrivial representation
In the mathematical field of representation theory, a trivial representation is a representation of a group G on which all elements of G act as the identity mapping of V...
of the trivial subgroup is the right regular representation
Regular representation
In mathematics, and in particular the theory of group representations, the regular representation of a group G is the linear representation afforded by the group action of G on itself by translation....
. More generally the induced representation of the trivial representation
Trivial representation
In the mathematical field of representation theory, a trivial representation is a representation of a group G on which all elements of G act as the identity mapping of V...
of any subgroup is the permutation representation on the cosets of that subgroup.
An induced representation of a one dimensional representation is called a monomial representation, because it can be represented as monomial matrices. Some groups have the property that all of their irreducible representations are monomial, the so-called monomial group
Monomial group
In mathematics, in the area of algebra studying the character theory of finite groups, an M-group or monomial group is a finite group whose complex irreducible characters are all monomial, that is, induced from characters of degree 1 ....
s.
In Lie theory, an extremely important example is parabolic induction
Parabolic induction
In mathematics, parabolic induction is a method of constructing representations of a reductive group from representations of its parabolic subgroups....
: inducing representations of a reductive group
Reductive group
In mathematics, a reductive group is an algebraic group G over an algebraically closed field such that the unipotent radical of G is trivial . Any semisimple algebraic group is reductive, as is any algebraic torus and any general linear group...
from representations of its parabolic subgroups. This leads, via the philosophy of cusp forms, to the Langlands program
Langlands program
The Langlands program is a web of far-reaching and influential conjectures that relate Galois groups in algebraic number theory to automorphic forms and representation theory of algebraic groups over local fields and adeles. It was proposed by ....
.