Reductive group
Encyclopedia
In mathematics
, a reductive group is an algebraic group
G over an algebraically closed field such that the unipotent radical of G is trivial (i.e., the group of unipotent elements of the radical
of G). Any semisimple algebraic group
is reductive, as is any algebraic torus
and any general linear group
. More generally, over fields that are not necessarily algebraically closed, a reductive group is a smooth affine algebraic group such that the unipotent radical of G over the algebraic closure is trivial. The intervention of an algebraic closure in this definition is necessary to include the case of imperfect ground fields, such as local and global function fields over finite fields.
The name comes from the complete reducibility
of linear representations of such a group, which is a property in fact holding over field
s of characteristic zero. Haboush's theorem shows that a certain rather weaker property holds for reductive groups in the general case.
If G ≤ GLn is a smooth closed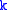
-subgroup that acts irreducibly on affine 
-space over 
, then G is reductive. It follows that GLn and SLn are reductive (the latter being even semisimple
).
s, a reductive Lie group G can be defined in terms of its Lie algebra
, namely a reductive Lie group is one whose Lie algebra g is a reductive Lie algebra; concretely, a Lie algebra that is the sum of an abelian and a semisimple Lie algebra. Sometimes the condition that identity component
G0 of G is of finite index is added.
A Lie algebra is reductive if and only if its adjoint representation
is completely reducible, but this does not imply that all of its finite dimensional representations are completely reducible. The concept of reductive is not quite the same for Lie groups as it is for algebraic groups because a reductive Lie group can be the group of real points of a unipotent algebraic group.
For example, the one-dimensional, abelian Lie algebra R is obviously reductive, and is the Lie algebra of both a reductive algebraic group Gm (the multiplicative group
of nonzero real numbers) and also a unipotent (non-reductive) algebraic group Ga (the additive group
of real numbers). These are not isomorphic as algebraic groups; at the Lie algebra level we see the same structure, but this is not enough to make any stronger assertion (essentially because the exponential map is not an algebraic function).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a reductive group is an algebraic group
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
G over an algebraically closed field such that the unipotent radical of G is trivial (i.e., the group of unipotent elements of the radical
Radical of an algebraic group
The radical of an algebraic group is the identity component of its maximal normal solvable subgroup.- External links :*, Encyclopaedia of Mathematics...
of G). Any semisimple algebraic group
Semisimple algebraic group
In mathematics, especially in the areas of abstract algebra and algebraic geometry studying linear algebraic groups, a semisimple algebraic group is a type of matrix group which behaves much like a semisimple Lie algebra or semisimple ring.- Definition :...
is reductive, as is any algebraic torus
Algebraic torus
In mathematics, an algebraic torus is a type of commutative affine algebraic group. These groups were named by analogy with the theory of tori in Lie group theory...
and any general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
. More generally, over fields that are not necessarily algebraically closed, a reductive group is a smooth affine algebraic group such that the unipotent radical of G over the algebraic closure is trivial. The intervention of an algebraic closure in this definition is necessary to include the case of imperfect ground fields, such as local and global function fields over finite fields.
The name comes from the complete reducibility
Semisimple algebraic group
In mathematics, especially in the areas of abstract algebra and algebraic geometry studying linear algebraic groups, a semisimple algebraic group is a type of matrix group which behaves much like a semisimple Lie algebra or semisimple ring.- Definition :...
of linear representations of such a group, which is a property in fact holding over field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
s of characteristic zero. Haboush's theorem shows that a certain rather weaker property holds for reductive groups in the general case.
If G ≤ GLn is a smooth closed
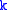-subgroup that acts irreducibly on affine -space over , then G is reductive. It follows that GLn and SLn are reductive (the latter being even semisimpleSemisimple algebraic group
In mathematics, especially in the areas of abstract algebra and algebraic geometry studying linear algebraic groups, a semisimple algebraic group is a type of matrix group which behaves much like a semisimple Lie algebra or semisimple ring.- Definition :...
).
Lie group case
More generally, in the case of Lie groupLie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s, a reductive Lie group G can be defined in terms of its Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
, namely a reductive Lie group is one whose Lie algebra g is a reductive Lie algebra; concretely, a Lie algebra that is the sum of an abelian and a semisimple Lie algebra. Sometimes the condition that identity component
Identity component
In mathematics, the identity component of a topological group G is the connected component G0 of G that contains the identity element of the group...
G0 of G is of finite index is added.
A Lie algebra is reductive if and only if its adjoint representation
Adjoint representation
In mathematics, the adjoint representation of a Lie group G is the natural representation of G on its own Lie algebra...
is completely reducible, but this does not imply that all of its finite dimensional representations are completely reducible. The concept of reductive is not quite the same for Lie groups as it is for algebraic groups because a reductive Lie group can be the group of real points of a unipotent algebraic group.
For example, the one-dimensional, abelian Lie algebra R is obviously reductive, and is the Lie algebra of both a reductive algebraic group Gm (the multiplicative group
Multiplicative group
In mathematics and group theory the term multiplicative group refers to one of the following concepts, depending on the context*any group \scriptstyle\mathfrak \,\! whose binary operation is written in multiplicative notation ,*the underlying group under multiplication of the invertible elements of...
of nonzero real numbers) and also a unipotent (non-reductive) algebraic group Ga (the additive group
Additive group
An additive group may refer to:*an abelian group, when it is written using the symbol + for its binary operation*a group scheme representing the underlying-additive-group functor...
of real numbers). These are not isomorphic as algebraic groups; at the Lie algebra level we see the same structure, but this is not enough to make any stronger assertion (essentially because the exponential map is not an algebraic function).