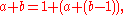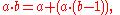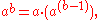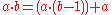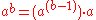Hyperoperation
Encyclopedia
In mathematics
, the hyperoperation sequence
is an infinite sequence
of arithmetic operations (called hyperoperations) that starts with the unary operation
of successor, then continues with the binary operation
s of addition
, multiplication
and exponentiation
, after which the sequence proceeds with further binary operations extending beyond exponentiation. For the operations beyond exponentiation, the nth member of this sequence is named by Reuben Goodstein
after the Greek prefix
of n suffixed with -ation (such as tetration
, pentation
) and can be written using n-2 arrows in Knuth's up-arrow notation
(if the latter is properly extended to negative arrow-indices for the first three hyperoperations).
Each hyperoperation is defined recursively
in terms of the previous one, according to the recursion
rule part
of the definition, as in Knuth's up-arrow version of the Ackermann function
:
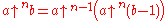
This recursion rule is common to many variants of hyperoperations (see below).
of binary operation
s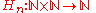 indexed by
indexed by 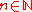 , defined recursively
, defined recursively
as follows:
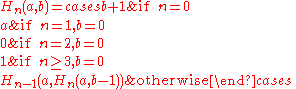
(Note that for n = 0, the binary operation
essentially reduces to a unary operation
by ignoring the first argument.)
For n = 0, 1, 2, 3, this definition reproduces the basic arithmetic operations of successor (which is a unary operation), addition
, multiplication
, and exponentiation
, respectively, as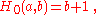
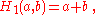
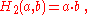
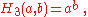
and for n ≥ 4 it extends these basic operations beyond exponentiation to what can be written in Knuth's up-arrow notation
as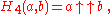

Knuth's notation could be extended to negative indices ≥ -2 in such a way as to agree with the entire hyperoperation sequence, except for the lag in the indexing: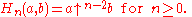
The hyperoperations can thus be seen as an answer to the question "what's next" in the sequence
: successor, addition
, multiplication
, exponentiation
, and so on. Noting that
the relationship between basic arithmetic operations is illustrated, allowing the higher operations to be defined naturally as above. The parameters of the hyperoperation hierarchy are sometimes referred to by their analogous exponentiation term; so a is the base, b is the exponent
(or hyperexponent), and n is the rank (or grade).
In common terms, the hyperoperations are ways of compounding numbers that increase in growth based on the iteration of the previous hyperoperation. The concepts of successor, addition, multiplication and exponentiation are all hyperoperations; the successor operation (producing x+1 from x) is the most primitive, the addition operator specifies the number of times 1 is to be added to itself to produce a final value, multiplication specifies the number of times a number is to be added to itself, and exponentiation refers to the number of times a number is to be multiplied by itself.
See also Tables of values.
defined the function
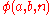
which somewhat resembles the hyperoperation sequence.
In his 1947 paper, R. L. Goodstein introduced the specific sequence of operations that are now called hyperoperations, and also suggested the Greek names tetration
, pentation, hexation, etc., for the extended operations beyond exponentiation (because they correspond to the indices 4, 5, 6, etc.). As a three-argument function, e.g.,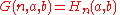 , the hyperoperation sequence as a whole is seen to be a version of the original Ackermann function
, the hyperoperation sequence as a whole is seen to be a version of the original Ackermann function
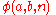 — recursive
— recursive
but not primitive recursive — as modified by Goodstein to incorporate the primitive successor function together with the other three basic operations of arithmetic (addition
, multiplication
, exponentiation
), and to make a more seamless extension of these beyond exponentiation.
The original three-argument Ackermann function
 uses the same recursion rule as does Goodstein's version of it (i.e., the hyperoperation sequence), but differs from it in two ways. First,
uses the same recursion rule as does Goodstein's version of it (i.e., the hyperoperation sequence), but differs from it in two ways. First, 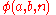 defines a sequence of operations starting from addition (n = 0) rather than the successor function, then multiplication (n = 1), exponentiation (n = 2), etc. Secondly, the initial conditions for
defines a sequence of operations starting from addition (n = 0) rather than the successor function, then multiplication (n = 1), exponentiation (n = 2), etc. Secondly, the initial conditions for 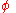 result in
result in 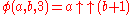 ,
,
thus differing from the hyperoperations beyond exponentiation. The significance of the b + 1 in the previous expression is that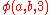 =
= 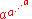 , where b counts the number of operators (exponentiations), rather than counting the number of operands ("a"s) as does the b in
, where b counts the number of operators (exponentiations), rather than counting the number of operands ("a"s) as does the b in  , and so on for the higher-level operations. (See the Ackermann function
, and so on for the higher-level operations. (See the Ackermann function
article for details.)
In the general sense, a hyperoperation hierarchy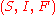 is a family
is a family
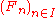 of binary operation
of binary operation
s on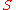 , indexed
, indexed
by a set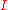 , such that there exists
, such that there exists  where
where
Also, if the last condition is relaxed (i.e. there is no exponentiation
), then we may also include the commutative hyperoperations, described below. Although one could list each hyperoperation explicitly, this is generally not the case. Most variants only include the successor function (or addition
) in their definition, and redefine multiplication
(and beyond) based on a single recursion rule that applies to all ranks. Since this is part of the definition of the hierarchy, and not a property of the hierarchy itself, it is difficult to define formally.
There are many possibilities for hyperoperations that are different from Goodstein's version. By using different initial conditions for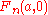 or
or 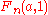 , the iterations of these conditions may produce different hyperoperations above exponentiation, while still corresponding to addition and multiplication. The modern definition of hyperoperations includes
, the iterations of these conditions may produce different hyperoperations above exponentiation, while still corresponding to addition and multiplication. The modern definition of hyperoperations includes 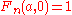 for all
for all  , whereas the variants below include
, whereas the variants below include 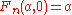 , and
, and 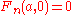 .
.
An open problem in hyperoperation research is whether the hyperoperation hierarchy can be generalized to
can be generalized to 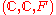 , and whether
, and whether 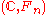 forms a quasigroup
forms a quasigroup
(with restricted domains).
Variant starting from
In 1928, Wilhelm Ackermann
defined a 3-argument function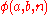 which gradually evolved into a 2-argument function known as the Ackermann function
which gradually evolved into a 2-argument function known as the Ackermann function
. The original Ackermann function was less similar to modern hyperoperations, because his initial conditions start with
was less similar to modern hyperoperations, because his initial conditions start with 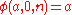 for all
for all  . Also he assigned addition to
. Also he assigned addition to 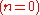 , multiplication to
, multiplication to 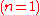 and exponentiation to
and exponentiation to 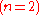 , so the initial conditions produce very different operations for tetration and beyond.
, so the initial conditions produce very different operations for tetration and beyond.
Another initial condition that has been used is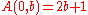 (where the base is constant
(where the base is constant  ), due to Rózsa Péter, which does not form a hyperoperation hierarchy.
), due to Rózsa Péter, which does not form a hyperoperation hierarchy.
overflows.
Since then, many other authors
have renewed interest in the application of hyperoperations to floating-point
representation.
While discussing tetration
, Clenshaw et al. assumed the initial condition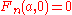 , which makes yet another hyperoperation hierarchy. Just like in the previous variant, the fourth operation is very similar to tetration
, which makes yet another hyperoperation hierarchy. Just like in the previous variant, the fourth operation is very similar to tetration
, but offset by one.
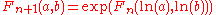
which is symmetric in a and b, meaning all hyperoperations are commutative. This sequence does not contain exponentiation
, and so does not form a hyperoperation hierarchy.
 , and are thus related to Steinhaus-Moser notation. The recursion rule used in balanced hyperoperations is
, and are thus related to Steinhaus-Moser notation. The recursion rule used in balanced hyperoperations is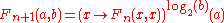
which requires continuous
iteration
, even for integer
b.
define (with ° or subscript)
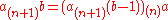
with
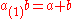 ,
,
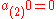 , and
, and
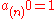
for

But this suffers a kind of collapse,
failing to form the "power tower" traditionally expected of hyper4:
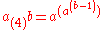
How can be so different from
be so different from 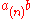 for n>3? This is because of a symmetry
for n>3? This is because of a symmetry
called associativity
that's defined into + and × (see field
) but which ^ lacks. Let's demonstrate this lack of associativity in exponentiation, which differentiates the higher and lower hyperoperations. Take for example the product: . This expression unambiguously evaluates to 24. However, if we replace the multiplication symbols with those of exponentiation, the expression becomes ambiguous. Do we mean
. This expression unambiguously evaluates to 24. However, if we replace the multiplication symbols with those of exponentiation, the expression becomes ambiguous. Do we mean 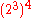 or
or 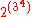 ? There is a big difference, since the former expression can be rewritten as
? There is a big difference, since the former expression can be rewritten as  while the latter is
while the latter is 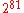 . In other words, left associative folds of the exponential operator on sequences do not coincide with right associative folds, the latter usually resulting in larger numbers. It is more apt to say the two (n)s were decreed to be the same for n<4. (On the other hand, one can object that the field operations were defined to mimic what had been "observed in nature" and ask why "nature" suddenly objects to that symmetry…)
. In other words, left associative folds of the exponential operator on sequences do not coincide with right associative folds, the latter usually resulting in larger numbers. It is more apt to say the two (n)s were decreed to be the same for n<4. (On the other hand, one can object that the field operations were defined to mimic what had been "observed in nature" and ask why "nature" suddenly objects to that symmetry…)
The other degrees do not collapse in this way, and so this family has some interest of its own as lower (perhaps lesser or inferior) hyperoperations. With hyperfunctions greater than three, it is also lower in the sense that the answers you get are actually often a lot lower than the answers you get when using the standard method.
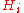 and
and  are said to coincide on
are said to coincide on 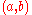 when
when 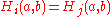 . For example, for all
. For example, for all  , i.e. all hyperoperations above addition,
, i.e. all hyperoperations above addition, 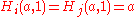 . Similarly,
. Similarly, 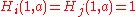 , but in this case both addition and mutiplication must be excluded. A point at which all hyperoperations coincide (excluding the unary successor function which does not really belong as a binary operation) is (2, 2) i.e. for all
, but in this case both addition and mutiplication must be excluded. A point at which all hyperoperations coincide (excluding the unary successor function which does not really belong as a binary operation) is (2, 2) i.e. for all 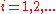 we have that
we have that 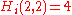 . There is a connection between the arity of these functions i.e. two and this point of coincidence: since the second argument of a hyperoperation is the length of the list on which to fold the previous operation, and this is 2, we get that the previous operation is folded over a list of length two, which amounts to applying it to the pair represented by that list. Also, since the first argument is itself 2, and this is duplicated in the recursion, we arrive again at the pair (2, 2) with each recursion. This happens until we get to 2 + 2 = 4.
. There is a connection between the arity of these functions i.e. two and this point of coincidence: since the second argument of a hyperoperation is the length of the list on which to fold the previous operation, and this is 2, we get that the previous operation is folded over a list of length two, which amounts to applying it to the pair represented by that list. Also, since the first argument is itself 2, and this is duplicated in the recursion, we arrive again at the pair (2, 2) with each recursion. This happens until we get to 2 + 2 = 4.
To be more precise, we have that =
= 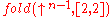 =
= 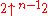 . Note that the unit of
. Note that the unit of 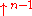 need not be supplied to fold when the list has length > 1. To demonstrate this recursion by means of an example we take
need not be supplied to fold when the list has length > 1. To demonstrate this recursion by means of an example we take 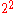 , which is two by itself twice i.e.
, which is two by itself twice i.e.  . This, in turn is two plus itself twice i.e.
. This, in turn is two plus itself twice i.e.  . At +, the recursion terminates and we are left with four.
. At +, the recursion terminates and we are left with four.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the hyperoperation sequence
is an infinite sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of arithmetic operations (called hyperoperations) that starts with the unary operation
Unary operation
In mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
of successor, then continues with the binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
s of addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
, multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
and exponentiation
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
, after which the sequence proceeds with further binary operations extending beyond exponentiation. For the operations beyond exponentiation, the nth member of this sequence is named by Reuben Goodstein
Reuben Goodstein
Reuben Louis Goodstein was an English mathematician with a strong interest in the philosophy and teaching of mathematics....
after the Greek prefix
Numerical prefix
Number prefixes are prefixes derived from numbers or numerals. In English and other European languages, they are used to coin numerous series of words, such as unicycle – bicycle – tricycle, dyad – triad – decade, biped – quadruped, September – October – November – December, decimal – hexadecimal,...
of n suffixed with -ation (such as tetration
Tetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
, pentation
Pentation
Pentation is the operation of repeated tetration, just as tetration is the operation of repeated exponentation and is a hyperoperation. It is non-commutative, and therefore has two inverse functions, which might be named the penta-root and the penta-logarithm...
) and can be written using n-2 arrows in Knuth's up-arrow notation
Knuth's up-arrow notation
In mathematics, Knuth's up-arrow notation is a method of notation for very large integers, introduced by Donald Knuth in 1976. It is closely related to the Ackermann function and especially to the hyperoperation sequence. The idea is based on the fact that multiplication can be viewed as iterated...
(if the latter is properly extended to negative arrow-indices for the first three hyperoperations).
Each hyperoperation is defined recursively
Recursion (computer science)
Recursion in computer science is a method where the solution to a problem depends on solutions to smaller instances of the same problem. The approach can be applied to many types of problems, and is one of the central ideas of computer science....
in terms of the previous one, according to the recursion
Recursion (computer science)
Recursion in computer science is a method where the solution to a problem depends on solutions to smaller instances of the same problem. The approach can be applied to many types of problems, and is one of the central ideas of computer science....
rule part
Piecewise
On mathematics, a piecewise-defined function is a function whose definition changes depending on the value of the independent variable...
of the definition, as in Knuth's up-arrow version of the Ackermann function
Ackermann function
In computability theory, the Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest-discovered examples of a total computable function that is not primitive recursive...
:
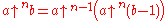
This recursion rule is common to many variants of hyperoperations (see below).
Definition
The hyperoperation sequence is the sequenceSequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
s
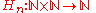 indexed by
indexed by 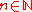 , defined recursively
, defined recursivelyRecursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
as follows:
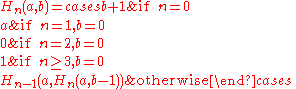
(Note that for n = 0, the binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
essentially reduces to a unary operation
Unary operation
In mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
by ignoring the first argument.)
For n = 0, 1, 2, 3, this definition reproduces the basic arithmetic operations of successor (which is a unary operation), addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
, multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
, and exponentiation
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
, respectively, as
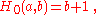
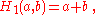
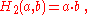
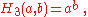
and for n ≥ 4 it extends these basic operations beyond exponentiation to what can be written in Knuth's up-arrow notation
Knuth's up-arrow notation
In mathematics, Knuth's up-arrow notation is a method of notation for very large integers, introduced by Donald Knuth in 1976. It is closely related to the Ackermann function and especially to the hyperoperation sequence. The idea is based on the fact that multiplication can be viewed as iterated...
as
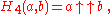

- ...
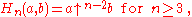
- ...
Knuth's notation could be extended to negative indices ≥ -2 in such a way as to agree with the entire hyperoperation sequence, except for the lag in the indexing:
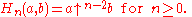
The hyperoperations can thus be seen as an answer to the question "what's next" in the sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
: successor, addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
, multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
, exponentiation
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
, and so on. Noting that
the relationship between basic arithmetic operations is illustrated, allowing the higher operations to be defined naturally as above. The parameters of the hyperoperation hierarchy are sometimes referred to by their analogous exponentiation term; so a is the base, b is the exponent
(or hyperexponent), and n is the rank (or grade).
In common terms, the hyperoperations are ways of compounding numbers that increase in growth based on the iteration of the previous hyperoperation. The concepts of successor, addition, multiplication and exponentiation are all hyperoperations; the successor operation (producing x+1 from x) is the most primitive, the addition operator specifies the number of times 1 is to be added to itself to produce a final value, multiplication specifies the number of times a number is to be added to itself, and exponentiation refers to the number of times a number is to be multiplied by itself.
Examples
This is a list of the first seven hyperoperations.| n | Operation | Definition | Names | Domain |
|---|---|---|---|---|
| 0 |  |
 |
hyper0, increment, successor, zeration | b arbitrary |
| 1 |  |
 |
hyper1, addition Addition Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples.... |
arbitrary |
| 2 |  |
 |
hyper2, multiplication Multiplication Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic .... |
arbitrary |
| 3 | 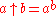 |
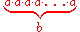 |
hyper3, exponentiation Exponentiation Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n... |
a > 0, b real, or a non-zero, b an integer, with some multivalued extensions to complex numbers |
| 4 |  |
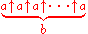 |
hyper4, tetration Tetration In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers... |
a > 0, b an integer ≥ −1 (with some proposed extensions) |
| 5 |  or or 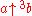 |
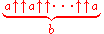 |
hyper5, pentation Pentation Pentation is the operation of repeated tetration, just as tetration is the operation of repeated exponentation and is a hyperoperation. It is non-commutative, and therefore has two inverse functions, which might be named the penta-root and the penta-logarithm... |
a and b integers, a > 0, b ≥ 0 |
| 6 |  |
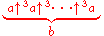 |
hyper6, hexation | a and b integers, a > 0, b ≥ 0 |
See also Tables of values.
History
One of the earliest discussions of hyperoperations was that of Albert Bennett in 1914, who developed some of the theory of commutative hyperoperations (see below). About 12 years later, Wilhelm AckermannWilhelm Ackermann
Wilhelm Friedrich Ackermann was a German mathematician best known for the Ackermann function, an important example in the theory of computation....
defined the function
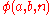
which somewhat resembles the hyperoperation sequence.
In his 1947 paper, R. L. Goodstein introduced the specific sequence of operations that are now called hyperoperations, and also suggested the Greek names tetration
Tetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
, pentation, hexation, etc., for the extended operations beyond exponentiation (because they correspond to the indices 4, 5, 6, etc.). As a three-argument function, e.g.,
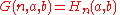 , the hyperoperation sequence as a whole is seen to be a version of the original Ackermann function
, the hyperoperation sequence as a whole is seen to be a version of the original Ackermann functionAckermann function
In computability theory, the Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest-discovered examples of a total computable function that is not primitive recursive...
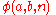 — recursive
— recursiveComputable function
Computable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
but not primitive recursive — as modified by Goodstein to incorporate the primitive successor function together with the other three basic operations of arithmetic (addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
, multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
, exponentiation
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
), and to make a more seamless extension of these beyond exponentiation.
The original three-argument Ackermann function
Ackermann function
In computability theory, the Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest-discovered examples of a total computable function that is not primitive recursive...
 uses the same recursion rule as does Goodstein's version of it (i.e., the hyperoperation sequence), but differs from it in two ways. First,
uses the same recursion rule as does Goodstein's version of it (i.e., the hyperoperation sequence), but differs from it in two ways. First, 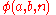 defines a sequence of operations starting from addition (n = 0) rather than the successor function, then multiplication (n = 1), exponentiation (n = 2), etc. Secondly, the initial conditions for
defines a sequence of operations starting from addition (n = 0) rather than the successor function, then multiplication (n = 1), exponentiation (n = 2), etc. Secondly, the initial conditions for 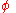 result in
result in 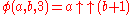 ,
,thus differing from the hyperoperations beyond exponentiation. The significance of the b + 1 in the previous expression is that
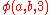 =
= 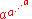 , where b counts the number of operators (exponentiations), rather than counting the number of operands ("a"s) as does the b in
, where b counts the number of operators (exponentiations), rather than counting the number of operands ("a"s) as does the b in  , and so on for the higher-level operations. (See the Ackermann function
, and so on for the higher-level operations. (See the Ackermann functionAckermann function
In computability theory, the Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest-discovered examples of a total computable function that is not primitive recursive...
article for details.)
Notations
This is a list of notations that have been used for hyperoperations.| Name | Notation equivalent to 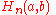 |
Comment |
|---|---|---|
| Knuth's up-arrow notation Knuth's up-arrow notation In mathematics, Knuth's up-arrow notation is a method of notation for very large integers, introduced by Donald Knuth in 1976. It is closely related to the Ackermann function and especially to the hyperoperation sequence. The idea is based on the fact that multiplication can be viewed as iterated... |
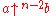 |
Used by Knuth (for n ≥ 2), and found in several reference books. |
| Goodstein's notation | 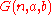 |
Used by Reuben Goodstein Reuben Goodstein Reuben Louis Goodstein was an English mathematician with a strong interest in the philosophy and teaching of mathematics.... . |
| Original Ackermann function Ackermann function In computability theory, the Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest-discovered examples of a total computable function that is not primitive recursive... |
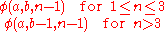 |
Used by Wilhelm Ackermann Wilhelm Ackermann Wilhelm Friedrich Ackermann was a German mathematician best known for the Ackermann function, an important example in the theory of computation.... . |
| Ackermann–Péter function Ackermann function In computability theory, the Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest-discovered examples of a total computable function that is not primitive recursive... |
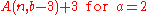 |
This corresponds to hyperoperations for base 2. |
| Nambiar's notation |  |
Used by Nambiar |
| Box notation | Used by Rubtsov and Romerio. | |
| Superscript notation | 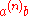 |
Used by Robert Munafo. |
| Subscript notation | 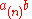 |
Used for lower hyperoperations by Robert Munafo. |
| Square bracket notation |  |
Used in many online forums; convenient for ASCII. |
Generalization
For different initial conditions or different recursion rules, very different operations can occur. Some mathematicians refer to all variants as examples of hyperoperations.In the general sense, a hyperoperation hierarchy
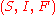 is a family
is a familyIndexed family
In mathematics, an indexed family is a collection of values that are associated with indexes. For example, a family of real numbers, indexed by the integers is a collection of real numbers, where each integer is associated with one of the real numbers....
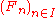 of binary operation
of binary operationBinary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
s on
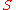 , indexed
, indexedIndex set
In mathematics, the elements of a set A may be indexed or labeled by means of a set J that is on that account called an index set...
by a set
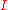 , such that there exists
, such that there exists  where
where
-
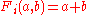 (additionAdditionAddition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
(additionAdditionAddition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
), -
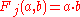 (multiplicationMultiplicationMultiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
(multiplicationMultiplicationMultiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
), and -
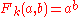 (exponentiationExponentiationExponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
(exponentiationExponentiationExponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
).
Also, if the last condition is relaxed (i.e. there is no exponentiation
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
), then we may also include the commutative hyperoperations, described below. Although one could list each hyperoperation explicitly, this is generally not the case. Most variants only include the successor function (or addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
) in their definition, and redefine multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
(and beyond) based on a single recursion rule that applies to all ranks. Since this is part of the definition of the hierarchy, and not a property of the hierarchy itself, it is difficult to define formally.
There are many possibilities for hyperoperations that are different from Goodstein's version. By using different initial conditions for
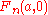 or
or 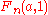 , the iterations of these conditions may produce different hyperoperations above exponentiation, while still corresponding to addition and multiplication. The modern definition of hyperoperations includes
, the iterations of these conditions may produce different hyperoperations above exponentiation, while still corresponding to addition and multiplication. The modern definition of hyperoperations includes 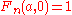 for all
for all  , whereas the variants below include
, whereas the variants below include 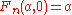 , and
, and 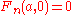 .
.An open problem in hyperoperation research is whether the hyperoperation hierarchy
 can be generalized to
can be generalized to 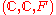 , and whether
, and whether 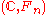 forms a quasigroup
forms a quasigroupQuasigroup
In mathematics, especially in abstract algebra, a quasigroup is an algebraic structure resembling a group in the sense that "division" is always possible...
(with restricted domains).
Variant starting from 
In 1928, Wilhelm AckermannWilhelm Ackermann
Wilhelm Friedrich Ackermann was a German mathematician best known for the Ackermann function, an important example in the theory of computation....
defined a 3-argument function
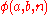 which gradually evolved into a 2-argument function known as the Ackermann function
which gradually evolved into a 2-argument function known as the Ackermann functionAckermann function
In computability theory, the Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest-discovered examples of a total computable function that is not primitive recursive...
. The original Ackermann function
 was less similar to modern hyperoperations, because his initial conditions start with
was less similar to modern hyperoperations, because his initial conditions start with 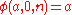 for all
for all  . Also he assigned addition to
. Also he assigned addition to 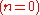 , multiplication to
, multiplication to 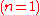 and exponentiation to
and exponentiation to 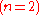 , so the initial conditions produce very different operations for tetration and beyond.
, so the initial conditions produce very different operations for tetration and beyond.| n | Operation | Comment |
|---|---|---|
| 0 | 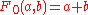 |
|
| 1 | 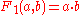 |
|
| 2 | 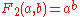 |
|
| 3 | 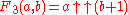 |
An offset form of tetration Tetration In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers... . The iteration of this operation is much different than the iteration Iterated function In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated... of tetration. |
| 4 | 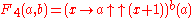 |
Not to be confused with pentation Pentation Pentation is the operation of repeated tetration, just as tetration is the operation of repeated exponentation and is a hyperoperation. It is non-commutative, and therefore has two inverse functions, which might be named the penta-root and the penta-logarithm... . |
Another initial condition that has been used is
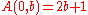 (where the base is constant
(where the base is constant  ), due to Rózsa Péter, which does not form a hyperoperation hierarchy.
), due to Rózsa Péter, which does not form a hyperoperation hierarchy.Variant starting from 0
In 1984, C. W. Clenshaw and F. W. J. Olver began the discussion of using hyperoperations to prevent computer floating-pointFloating point
In computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
overflows.
Since then, many other authors
have renewed interest in the application of hyperoperations to floating-point
Floating point
In computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
representation.
While discussing tetration
Tetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
, Clenshaw et al. assumed the initial condition
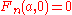 , which makes yet another hyperoperation hierarchy. Just like in the previous variant, the fourth operation is very similar to tetration
, which makes yet another hyperoperation hierarchy. Just like in the previous variant, the fourth operation is very similar to tetrationTetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
, but offset by one.
| n | Operation | Comment |
|---|---|---|
| 1 | 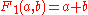 |
|
| 2 | 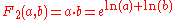 |
|
| 3 | 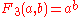 |
|
| 4 | 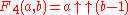 |
An offset form of tetration Tetration In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers... . The iteration of this operation is much different than the iteration Iterated function In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated... of tetration Tetration In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers... . |
| 5 | 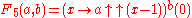 |
Not to be confused with pentation Pentation Pentation is the operation of repeated tetration, just as tetration is the operation of repeated exponentation and is a hyperoperation. It is non-commutative, and therefore has two inverse functions, which might be named the penta-root and the penta-logarithm... . |
Commutative hyperoperations
Commutative hyperoperations were considered by Albert Bennett as early as 1914, which is possibly the earliest remark about any hyperoperation sequence. Commutative hyperoperations are defined by the recursion rule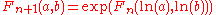
which is symmetric in a and b, meaning all hyperoperations are commutative. This sequence does not contain exponentiation
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
, and so does not form a hyperoperation hierarchy.
| n | Operation | Comment |
|---|---|---|
| 0 | 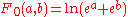 |
|
| 1 | 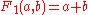 |
|
| 2 | 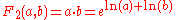 |
This is due to the properties of the logarithm. |
| 3 | 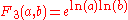 |
A commutative Commutativity In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it... form of exponentiation Exponentiation Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n... . |
| 4 | 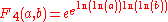 |
Not to be confused with tetration Tetration In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers... . |
Balanced hyperoperations
Balanced hyperoperations, first considered by Clément Frappier in 1991, are based on the iteration of the function , and are thus related to Steinhaus-Moser notation. The recursion rule used in balanced hyperoperations is
, and are thus related to Steinhaus-Moser notation. The recursion rule used in balanced hyperoperations is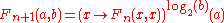
which requires continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
iteration
Iteration
Iteration means the act of repeating a process usually with the aim of approaching a desired goal or target or result. Each repetition of the process is also called an "iteration," and the results of one iteration are used as the starting point for the next iteration.-Mathematics:Iteration in...
, even for integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
b.
| n | Operation | Comment |
|---|---|---|
| 0 | Rank 0 does not exist. If there was a rank 0 balanced hyperoperation 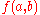 , then addition would be , then addition would be 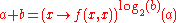 . Substituting . Substituting  in this equation gives in this equation gives 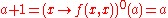 which is a contradiction. which is a contradiction. |
|
| 1 | 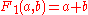 |
|
| 2 |  |
|
| 3 | 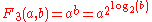 |
This is exponentiation Exponentiation Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n... . |
| 4 | 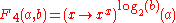 |
Not to be confused with tetration Tetration In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers... . |
Lower hyperoperations
An alternative for these hyperoperations is obtained by evaluation from left to right. Sincedefine (with ° or subscript)
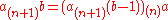
with
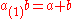 ,
,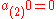 , and
, and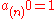
for

But this suffers a kind of collapse,
failing to form the "power tower" traditionally expected of hyper4:
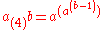
How can
 be so different from
be so different from 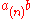 for n>3? This is because of a symmetry
for n>3? This is because of a symmetrySymmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
called associativity
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
that's defined into + and × (see field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
) but which ^ lacks. Let's demonstrate this lack of associativity in exponentiation, which differentiates the higher and lower hyperoperations. Take for example the product:
 . This expression unambiguously evaluates to 24. However, if we replace the multiplication symbols with those of exponentiation, the expression becomes ambiguous. Do we mean
. This expression unambiguously evaluates to 24. However, if we replace the multiplication symbols with those of exponentiation, the expression becomes ambiguous. Do we mean 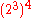 or
or 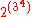 ? There is a big difference, since the former expression can be rewritten as
? There is a big difference, since the former expression can be rewritten as  while the latter is
while the latter is 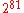 . In other words, left associative folds of the exponential operator on sequences do not coincide with right associative folds, the latter usually resulting in larger numbers. It is more apt to say the two (n)s were decreed to be the same for n<4. (On the other hand, one can object that the field operations were defined to mimic what had been "observed in nature" and ask why "nature" suddenly objects to that symmetry…)
. In other words, left associative folds of the exponential operator on sequences do not coincide with right associative folds, the latter usually resulting in larger numbers. It is more apt to say the two (n)s were decreed to be the same for n<4. (On the other hand, one can object that the field operations were defined to mimic what had been "observed in nature" and ask why "nature" suddenly objects to that symmetry…)The other degrees do not collapse in this way, and so this family has some interest of its own as lower (perhaps lesser or inferior) hyperoperations. With hyperfunctions greater than three, it is also lower in the sense that the answers you get are actually often a lot lower than the answers you get when using the standard method.
| n | Operation | Comment |
|---|---|---|
| 0 |  |
increment, successor, zeration |
| 1 | 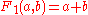 |
|
| 2 | 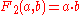 |
|
| 3 | 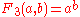 |
This is exponentiation Exponentiation Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n... . |
| 4 | 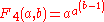 |
Not to be confused with tetration Tetration In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers... . |
| 5 | 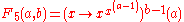 |
Not to be confused with pentation Pentation Pentation is the operation of repeated tetration, just as tetration is the operation of repeated exponentation and is a hyperoperation. It is non-commutative, and therefore has two inverse functions, which might be named the penta-root and the penta-logarithm... . |
Coincidence of Hyperoperations
Hyperoperations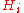 and
and  are said to coincide on
are said to coincide on 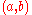 when
when 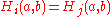 . For example, for all
. For example, for all  , i.e. all hyperoperations above addition,
, i.e. all hyperoperations above addition, 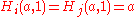 . Similarly,
. Similarly, 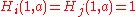 , but in this case both addition and mutiplication must be excluded. A point at which all hyperoperations coincide (excluding the unary successor function which does not really belong as a binary operation) is (2, 2) i.e. for all
, but in this case both addition and mutiplication must be excluded. A point at which all hyperoperations coincide (excluding the unary successor function which does not really belong as a binary operation) is (2, 2) i.e. for all 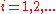 we have that
we have that 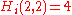 . There is a connection between the arity of these functions i.e. two and this point of coincidence: since the second argument of a hyperoperation is the length of the list on which to fold the previous operation, and this is 2, we get that the previous operation is folded over a list of length two, which amounts to applying it to the pair represented by that list. Also, since the first argument is itself 2, and this is duplicated in the recursion, we arrive again at the pair (2, 2) with each recursion. This happens until we get to 2 + 2 = 4.
. There is a connection between the arity of these functions i.e. two and this point of coincidence: since the second argument of a hyperoperation is the length of the list on which to fold the previous operation, and this is 2, we get that the previous operation is folded over a list of length two, which amounts to applying it to the pair represented by that list. Also, since the first argument is itself 2, and this is duplicated in the recursion, we arrive again at the pair (2, 2) with each recursion. This happens until we get to 2 + 2 = 4.To be more precise, we have that
 =
= 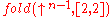 =
= 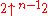 . Note that the unit of
. Note that the unit of 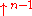 need not be supplied to fold when the list has length > 1. To demonstrate this recursion by means of an example we take
need not be supplied to fold when the list has length > 1. To demonstrate this recursion by means of an example we take 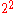 , which is two by itself twice i.e.
, which is two by itself twice i.e.  . This, in turn is two plus itself twice i.e.
. This, in turn is two plus itself twice i.e.  . At +, the recursion terminates and we are left with four.
. At +, the recursion terminates and we are left with four.