Tetration - AbsoluteAstronomy.com

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, tetration (also known as hyper-4) is an iterated exponential and is the next hyper operator after exponentiation

Exponentiation

Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...

. The word tetration was coined by English mathematician

Mathematician

A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....

Reuben Louis Goodstein from tetra- (four) and iteration

Iterated function

In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...

. Tetration is used for the notation of very large numbers. Shown here are examples of the first four hyper operators, with tetration as the fourth (and succession, the unary operation denoted

taking

and yielding the number after

, as the 0th):

Addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....

a succeeded n times.
Multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....

a added to itself, n times.
Exponentiation

a multiplied by itself, n times.
Tetration

a exponentiated by itself, n times.

where each operation is defined by iterating the previous one (the next operation in the sequence is pentation

Pentation

Pentation is the operation of repeated tetration, just as tetration is the operation of repeated exponentation and is a hyperoperation. It is non-commutative, and therefore has two inverse functions, which might be named the penta-root and the penta-logarithm...

). The peculiarity of the tetration among these operations is that the first three (addition, multiplication and exponentiation) are generalized for complex

Complex number

A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

values of n, while for tetration, no such regular generalization is yet established; and tetration is not considered an elementary function.

Addition (a + n) is the most basic operation, multiplication (an) is also a primary operation, though for natural numbers it can be thought of as a chained addition involving n numbers a, and exponentiation (

) can be thought of as a chained multiplication involving n numbers a. Analogously, tetration (

) can be thought of as a chained power involving n numbers a. The parameter a may be called the base-parameter in the following, while the parameter n in the following may be called the height-parameter (which is integral in the first approach but may be generalized to fractional, real and complex heights, see below).

Definition

For any positive real

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

and non-negative integer

Integer

The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

, we define

by:

Iterated powers

As we can see from the definition, when evaluating tetration expressed as an "exponentiation tower", the exponentiation is done at the deepest level first (in the notation, at the highest level). In other words:

Note that exponentiation is not associative, so evaluating the expression in the other order will lead to a different answer:

Thus, the exponential towers must be evaluated from top to bottom (or right to left). Computer programmers refer to this choice as right-associative.

When a and n are coprime

Coprime

In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...

, we can compute the last m decimal digits of

using Euler's Theorem.

Terminology

There are many terms for tetration, each of which has some logic behind it, but some have not become commonly used for one reason or another. Here is a comparison of each term with its rationale and counter-rationale.

The term tetration, introduced by Goodstein in his 1947 paper Transfinite Ordinals in Recursive Number Theory (generalizing the recursive base-representation used in Goodstein's theorem
Goodstein's theorem
In mathematical logic, Goodstein's theorem is a statement about the natural numbers, made by Reuben Goodstein, which states that every Goodstein sequence eventually terminates at 0. showed that it is unprovable in Peano arithmetic...

to use higher operations), has gained dominance. It was also popularized in Rudy Rucker's Infinity and the Mind
Infinity and the Mind
Infinity and the Mind: The Science and Philosophy of the Infinite is a theoretical mathematics book by American mathematician, computer scientist, and science fiction writer Rudy Rucker.- Marketing :...

.
The term superexponentiation was published by Bromer in his paper Superexponentiation in 1987. It was used earlier by Ed Nelson in his book Predicative Arithmetic, Princeton University Press, 1986.
The term hyperpower is a natural combination of hyper and power, which aptly describes tetration. The problem lies in the meaning of hyper with respect to the hyper operator hierarchy. When considering hyper operators, the term hyper refers to all ranks, and the term super refers to rank 4, or tetration. So under these considerations hyperpower is misleading, since it is only referring to tetration.
The term power tower is occasionally used, in the form "the power tower of order n" for

Tetration is often confused with closely related functions and expressions. This is because much of the terminology that is used with them can be used with tetration. Here are a few related terms:

Form	Terminology
	Tetration
	Iterated exponentials
	Nested exponentials (also towers)
	Infinite exponentials (also towers)

In the first two expressions a is the base, and the number of times a appears is the height (add one for x). In the third expression, n is the height, but each of the bases is different.

Care must be taken when referring to iterated exponentials, as it is common to call expressions of this form iterated exponentiation, which is ambiguous, as this can either mean iterated

Iterated function

powers or iterated exponentials

Exponential function

In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...

Notation

There are many different notation styles that can be used to express tetration. Some of these styles can be used for higher iterations as well (hyper-5, hyper-6, and so on).

Name	Form	Description
Standard notation		Used by Maurer [1901] and Goodstein [1947]; Rudy Rucker Rudy Rucker Rudolf von Bitter Rucker is an American mathematician, computer scientist, science fiction author, and philosopher, and is one of the founders of the cyberpunk literary movement. The author of both fiction and non-fiction, he is best known for the novels in the Ware Tetralogy, the first two of... 's book Infinity and the Mind Infinity and the Mind Infinity and the Mind: The Science and Philosophy of the Infinite is a theoretical mathematics book by American mathematician, computer scientist, and science fiction writer Rudy Rucker.- Marketing :... popularized the notation.
Knuth's up-arrow notation Knuth's up-arrow notation In mathematics, Knuth's up-arrow notation is a method of notation for very large integers, introduced by Donald Knuth in 1976. It is closely related to the Ackermann function and especially to the hyperoperation sequence. The idea is based on the fact that multiplication can be viewed as iterated...		Allows extension by putting more arrows, or, even more powerfully, an indexed arrow.
Conway chained arrow notation Conway chained arrow notation Conway chained arrow notation, created by mathematician John Horton Conway, is a means of expressing certain extremely large numbers. It is simply a finite sequence of positive integers separated by rightward arrows, e.g. 2 → 3 → 4 → 5 → 6.As with most...		Allows extension by increasing the number 2 (equivalent with the extensions above), but also, even more powerfully, by extending the chain
Ackermann function Ackermann function In computability theory, the Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest-discovered examples of a total computable function that is not primitive recursive...		Allows the special case to be written in terms of the Ackermann function.
Iterated exponential notation		Allows simple extension to iterated exponentials from initial values other than 1.
Hooshmand notation
Hyper operator notation		Allows extension by increasing the number 4; this gives the family of hyper operations
ASCII ASCII The American Standard Code for Information Interchange is a character-encoding scheme based on the ordering of the English alphabet. ASCII codes represent text in computers, communications equipment, and other devices that use text... notation	`a^^n`	Since the up-arrow is used identically to the caret (`^`), the tetration operator may be written as (`^^`).

One notation above uses iterated exponential notation; in general this is defined as follows:

with n "a"s.

There are not as many notations for iterated exponentials, but here are a few:

Name	Form	Description
Standard notation		Euler coined the notation , and iteration notation has been around about as long.
Knuth's up-arrow notation		Allows for super-powers and super-exponential function by increasing the number of arrows; used in the article on large numbers Large numbers This article is about large numbers in the sense of numbers that are significantly larger than those ordinarily used in everyday life, for instance in simple counting or in monetary transactions... .
Ioannis Galidakis' notation		Allows for large expressions in the base.
ASCII (auxiliary)	`a^^n@x`	Based on the view that an iterated exponential is auxiliary tetration.
ASCII (standard)	`exp_a^n(x)`	Based on standard notation.
J Notation	`x^^:(n-1)x`	Repeats the exponentiation. See J (programming language) J (programming language) The J programming language, developed in the early 1990s by Kenneth E. Iverson and Roger Hui, is a synthesis of APL and the FP and FL function-level languages created by John Backus....

Examples

In the following table, most values are too large to write in scientific notation, so iterated exponential notation is employed to express them in base 10. The values containing a decimal point are approximate.


1	1	1	1
2	4	16	65,536
3	27	7,625,597,484,987
4	256
5	3,125
6	46,656
7	823,543
8	16,777,216
9	387,420,489
10	10,000,000,000

Linear approximation

A linear approximation (solution to the continuity requirement, approximation to the differentiability requirement) is given by:

hence:

Approximation	Domain
	for
	for
	for

and so on. However, it is only piecewise differentiable; at integer values of x the derivative is multiplied by

Examples

A main theorem in Hooshmand's paper states: Let

. If

is continuous and satisfies the conditions:

,
is differentiable on ,
is a nondecreasing or nonincreasing function on

then

is uniquely determined through the equation

,

where

denotes the fractional part of x and

is the

-iterated function

Iterated function

of the function

.

The proof is that the second through fourth conditions trivially imply that f is a linear function on [-1, 0].

The linear approximation to natural tetration function

is continuously differentiable, but its second derivative does not exist at integer values of its argument. Hooshmand derived another uniqueness theorem for it which states:

If

is a continuous function that satisfies:

,
is convex on ,

then

. [Here

is Hooshmand's name for the linear approximation to the natural tetration function.]

The proof is much the same as before; the recursion equation ensures that

and then the convexity condition implies that

is linear on (-1, 0).

Therefore the linear approximation to natural tetration is the only solution of the equation

and

which is convex

Convex function

In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...

. All other sufficiently-differentiable solutions must have an inflection point

Inflection point

In differential calculus, an inflection point, point of inflection, or inflection is a point on a curve at which the curvature or concavity changes sign. The curve changes from being concave upwards to concave downwards , or vice versa...

on the interval (-1, 0).

Higher order approximations

A quadratic approximation (to the differentiability requirement) is given by:

which is differentiable for all

, but not twice differentiable. If

this is the same as the linear approximation.

A cubic approximation and a method for generalizing to approximations of degree n are given at.

Extensions

Tetration can be extended to define

and other domains as well.

Extension to base zero

The exponential

is non consistently defined. Thus, the tetrations

are not clearly defined by the formula given earlier. However,

is well defined, and exists:

Thus we could consistently define

. This is equivalent to defining

.

Under this extension,

, so the rule

from the original definition still holds.

Extension to complex bases

Since complex number

Complex number

s can be raised to powers, tetration can be applied to bases of the form

, where

is the square root

Square root

In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...

of −1. For example,

where

, tetration is achieved by using the principal branch

Principal branch

In mathematics, a principal branch is a function which selects one branch, or "slice", of a multi-valued function. Most often, this applies to functions defined on the complex plane: see branch cut....

of the natural logarithm, and using Euler's formula

Euler's formula

Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...

we get the relation:

This suggests a recursive definition for

given any

The following approximate values can be derived:

	Approximate Value
	i

Solving the inverse relation as in the previous section, yields the expected

and

, with negative values of n giving infinite results on the imaginary axis. Plotted in the complex plane

Complex plane

In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...

, the entire sequence spirals to the limit

, which could be interpreted as the value where n is infinite.

Such tetration sequences have been studied since the time of Euler but are poorly understood due to their chaotic behavior. Most published research historically has focused on the convergence of the power tower function. Current research has greatly benefited by the advent of powerful computers with fractal and symbolic mathematics software. Much of what is known about tetration comes from general knowledge of complex dynamics and specific research of the exponential map.

Extension to infinite heights

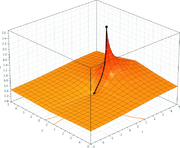
Tetration can be extended to infinite heights (n in

). This is because for bases within a certain interval, tetration converges to a finite value as the height tends to infinity

Infinity

Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...

. For example,

converges to 2, and can therefore be said to be equal to 2. The trend towards 2 can be seen by evaluating a small finite tower:

In general, the infinite power tower

, defined as the limit of

as n goes to infinity, converges for e^−e ≤ x ≤ e^1/e, roughly the interval from 0.066 to 1.44, a result shown by Leonhard Euler

Leonhard Euler

Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...

. The limit, should it exist, is a positive real solution of the equation y = x^y. Thus, x = y^1/y. The limit defining the infinite tetration of x fails to converge for x > e^1/e because the maximum of y^1/y is e^1/e.

This may be extended to complex numbers z with the definition:

where W(z) represents Lambert's W function.

As the limit y = ^∞x (if existent, i.e. for e^−e < x < e^1/e) must satisfy x^y = y we see that x ↦ y = ^∞x is (the lower branch of) the inverse function of y ↦ x = y^1/y.

(Limited) extension to negative heights

In order to preserve the original rule:

for negative values of

we must use the recursive relation:

Thus:

However smaller negative values cannot be well defined in this way because

which is not well defined.

Note further that for

any definition of

is consistent with the rule because

for any

Extension to real heights

At this time there is no commonly accepted solution to the general problem of extending tetration to the real or complex values of

. Various approaches are mentioned below.

In general the problem is finding, for any real a > 0, a super-exponential function

over real

that satisfies

for all real x > -1.
A fourth requirement that is usually one of:
A continuity requirement (usually just that is continuous in both variables for ).
A differentiability requirement (can be once, twice, k times, or infinitely differentiable in x).
A regularity requirement (implying twice differentiable in x) that:

for all

The fourth requirement differs from author to author, and between approaches. There are two main approaches to extending tetration to real heights, one is based on the regularity requirement, and one is based on the differentiability requirement. These two approaches seem to be so different that they may not be reconciled, as they produce results inconsistent with each other.

Fortunately, any solution that satisfies one of these in an interval of length one can be extended to a solution for all positive real numbers. When

is defined for an interval of length one, the whole function easily follows for all

Extension to complex heights

There is a conjecture

Conjecture

A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...

that there exists a unique function F which is a solution of the equation and satisfies the additional conditions that F(0)=1 and F(z) approaches the fixed points

Fixed point (mathematics)

In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...

of the logarithm (roughly 0.31813150520476413531 ± 1.33723570143068940890i)
as z approaches ±i∞ and that F is holomorphic in the whole complex z-plane, except the part of the real axis at z≤−2.
This function is shown in the figure at right.
The complex double precision approximation of this function is available online.
The requirement of holomorphism of tetration is important for the uniqueness. Many functions

can be constructed as

where

and

are real sequences which decay fast enough to provide the convergence of the series,
at least at moderate values of

.

The function S satisfies the tetration equations , S(0)=1, and if α_n and β_n approach 0 fast enough it will be analytic on a neighborhood of the positive real axis. However, if some elements of {α} or {β} are not zero, then function S has multitudes of additional singularities and cutlines in the complex plane, due to the exponential growth of sin and cos along the imaginary axis; the smaller the coefficients {α} and {β} are, the further away these singularities are from the real axis.

The extension of tetration into the complex plane is thus essential for the uniqueness; the real-analytic tetration is not unique.

Inverse relations

Exponentiation

Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...

has two inverse relations; roots

Nth root

In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...

and logarithms. Analogously, the inverse relation

Inverse function

In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...

s of tetration are often called the super-root, and the super-logarithm.

Super-root

The super-root is the inverse relation of tetration with respect to the base: if

, then y is an nth super root of x.
For example,

so 2 is the 4th super-root of 65,536 and

so 3 is the 3rd super-root (or super cube root) of 7,625,597,484,987.

Square super-root

The 2nd-order super-root, square super-root, or super square root has two equivalent notations,

and

. It is the inverse of

and can be represented with the Lambert W function:

Like square root

Square root

In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...

s, the square super-root of x may not have a single solution. Unlike square roots, determining the number of square super-roots of x may be difficult. In general, if

, then x has two positive square super-roots between 0 and 1; and if

, then x has one positive square super-root greater than 1. If x is positive and less than

it doesn't have any real

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

square super-roots, but the formula given above yields countably infinitely many complex

Complex number

ones for any finite x not equal to 1.

It is thought that if the square super-root of an integer is not an integer, it is irrational

Irrational number

In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....

, but it is unknown if there is any proof for this.

Other super-roots

For each integer , the function ⁿx is defined and increasing for , and , so that the nth super-root of x,

, exists for .

However, if the linear approximation above is used, then if -1 < y ≤ 0, so cannot exist.

Other super-roots are expressible under the same basis used with normal roots

Nth root

In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...

: super cube roots, the function that produces y when

, can be expressed as

; the 4th super-root can be expressed as

; and it can therefore be said that the n^th super-root is

. Note that

may not be uniquely defined, because there may be more than one n^th root. For example, x has a single (real) super-root if n is odd, and up to two if n is even.

The super-root can be extended to

, and this shows a link to the mathematical constant e

E (mathematical constant)

The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...

as it is only well-defined if 1/e ≤ x ≤ e (see extension of tetration to infinite heights). Note that

implies that

and thus that

. Therefore, when it is well defined,

and thus it is an elementary function. For example,

Super-logarithm

Once a continuous increasing (in x) definition of tetration, ^xa, is selected, the corresponding super-logarithm is defined for all real numbers x, and .

The function