
Homological integration
Encyclopedia
In the mathematical
fields of differential geometry and geometric measure theory
, homological integration or geometric integration is a method for extending the notion of the integral
to manifold
s. Rather than functions or differential form
s, the integral is defined over currents
on a manifold.
The theory is "homological" because currents themselves are defined by duality with differential forms. To wit, the space Dk of k-currents on a manifold M is defined as the dual space
, in the sense of distributions
, of the space of k-forms Ωk on M. Thus there is a pairing between k-currents T and k-forms α, denoted here by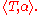
Under this duality pairing, the exterior derivative
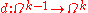
goes over to a boundary operator
defined by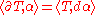
for all α ∈ Ωk. This is a homological rather than cohomological construction.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
fields of differential geometry and geometric measure theory
Geometric measure theory
In mathematics, geometric measure theory is the study of the geometric properties of the measures of sets , including such things as arc lengths and areas. It uses measure theory to generalize differential geometry to surfaces with mild singularities called rectifiable sets...
, homological integration or geometric integration is a method for extending the notion of the integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
to manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s. Rather than functions or differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s, the integral is defined over currents
Current (mathematics)
In mathematics, more particularly in functional analysis, differential topology, and geometric measure theory, a k-current in the sense of Georges de Rham is a functional on the space of compactly supported differential k-forms, on a smooth manifold M. Formally currents behave like Schwartz...
on a manifold.
The theory is "homological" because currents themselves are defined by duality with differential forms. To wit, the space Dk of k-currents on a manifold M is defined as the dual space
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
, in the sense of distributions
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
, of the space of k-forms Ωk on M. Thus there is a pairing between k-currents T and k-forms α, denoted here by
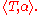
Under this duality pairing, the exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
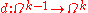
goes over to a boundary operator

defined by
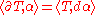
for all α ∈ Ωk. This is a homological rather than cohomological construction.

