
Hermitian function
Encyclopedia
In mathematical analysis
, a Hermitian function is a complex
function
with the property that its complex conjugate
is equal to the original function with the variable changed in sign
:
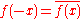
for all in the domain of
in the domain of  .
.
This definition extends also to functions of two or more variables, e.g., in the case that is a function of two variables it is Hermitian if
is a function of two variables it is Hermitian if
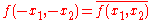
for all pairs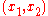 in the domain of
in the domain of  .
.
From this definition it follows immediately that, if is a Hermitian function, then
is a Hermitian function, then
Since the Fourier transform of a real signal is guaranteed to be Hermitian, it can be compressed using the Hermitian even/odd symmetry. This, for example, allows the discrete Fourier transform of a signal (which is in general complex) to be stored in the same space as the original real signal.
Where the is correlation
is correlation
, and is convolution
is convolution
. Because convolution is commutative we can infer also that:
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, a Hermitian function is a complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
with the property that its complex conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
is equal to the original function with the variable changed in sign
Sign (mathematics)
In mathematics, the word sign refers to the property of being positive or negative. Every nonzero real number is either positive or negative, and therefore has a sign. Zero itself is signless, although in some contexts it makes sense to consider a signed zero...
:
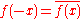
for all
 in the domain of
in the domain of  .
.This definition extends also to functions of two or more variables, e.g., in the case that
 is a function of two variables it is Hermitian if
is a function of two variables it is Hermitian if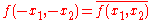
for all pairs
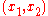 in the domain of
in the domain of  .
.From this definition it follows immediately that, if
 is a Hermitian function, then
is a Hermitian function, then- the real part of
 is an even function
is an even function - the imaginary part of
 is an odd function
is an odd function
Motivation
Hermitian functions appear frequently in mathematics, physics, and signal processing. For example, the following two statements follows from basic properties of the Fourier transform:- The function
 is real-valued if and only if the Fourier transformFourier transformIn mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
is real-valued if and only if the Fourier transformFourier transformIn mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of is Hermitian.
is Hermitian.
- The function
 is Hermitian if and only if the Fourier transformFourier transformIn mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
is Hermitian if and only if the Fourier transformFourier transformIn mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of is real-valued.
is real-valued.
Since the Fourier transform of a real signal is guaranteed to be Hermitian, it can be compressed using the Hermitian even/odd symmetry. This, for example, allows the discrete Fourier transform of a signal (which is in general complex) to be stored in the same space as the original real signal.
- If either f or g is Hermitian, then

Where the
 is correlation
is correlationCorrelation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
, and
 is convolution
is convolutionConvolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
. Because convolution is commutative we can infer also that:
- If either f or g is Hermitian, then
 , which in general is not true.
, which in general is not true.

