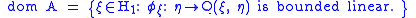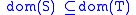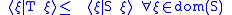Friedrichs extension
Encyclopedia
In functional analysis
, the Friedrichs extension is a canonical
self-adjoint
extension of a non-negative densely defined symmetric operator. It is named after the mathematician Kurt Friedrichs. This extension is particularly useful in situations where an operator may fail to be essentially self-adjoint or whose essential self-adjointness is difficult to show.
An operator T is non-negative if

Example. Let U be an open set in Rn. On L2(U) we consider differential operator
s of the form

where the functions ai j are infinitely differentiable real-valued functions on U. We consider T acting on the dense subspace of infinitely differentiable complex-valued functions of compact support, in symbols
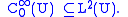
If for each x ∈ U the n × n matrix
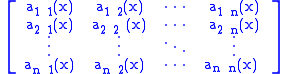
is non-negative semi-definite, then T is a non-negative operator. This means (a) that the matrix is hermitian
and
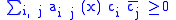
for every choice of complex numbers c1, ..., cn. This is proved using integration by parts
.
These operators are elliptic
although in general elliptic operators may not be non-negative. They are however bounded from below.
If T is non-negative, then
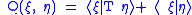
is a sesquilinear form on dom T and
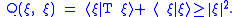
Thus Q defines an inner product on dom T. Let H1 be the completion
of dom T with respect to Q. H1 is an abstractly defined space; for instance its elements can be represented as equivalence classes of Cauchy sequence
s of elements of dom T. It is not obvious that all elements in H1 can identified with elements of H. However, the following can be proved:
The canonical inclusion

extends to an injective continuous map H1 → H. We regard H1 as a subspace of H.
Define an operator A by
In the above formula, bounded is relative to the topology on H1 inherited from H. By the Riesz representation theorem
applied to the linear functional φξ extended to H, there is a unique A ξ ∈ H such that
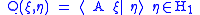
Theorem. A is a non-negative self-adjoint operator such that T1=A - I extends T.
T1 is the Friedrichs extension of T.
If T, S are non-negative operators, write

if, and only if,
Theorem. There are unique self-adjoint extensions Tmin and Tmax of any non-negative symmetric operator T such that

and every non-negative self-adjoint extension S of T is between Tmin and Tmax, i.e

The Friedrichs extension of T is Tmax.
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, the Friedrichs extension is a canonical
Canonical
Canonical is an adjective derived from canon. Canon comes from the greek word κανών kanon, "rule" or "measuring stick" , and is used in various meanings....
self-adjoint
Self-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
extension of a non-negative densely defined symmetric operator. It is named after the mathematician Kurt Friedrichs. This extension is particularly useful in situations where an operator may fail to be essentially self-adjoint or whose essential self-adjointness is difficult to show.
An operator T is non-negative if

Examples
Example. Multiplication by a non-negative function on an L2 space is a non-negative self-adjoint operator.Example. Let U be an open set in Rn. On L2(U) we consider differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
s of the form

where the functions ai j are infinitely differentiable real-valued functions on U. We consider T acting on the dense subspace of infinitely differentiable complex-valued functions of compact support, in symbols
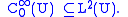
If for each x ∈ U the n × n matrix
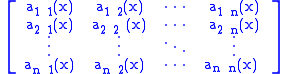
is non-negative semi-definite, then T is a non-negative operator. This means (a) that the matrix is hermitian
Hermitian
A number of mathematical entities are named Hermitian, after the mathematician Charles Hermite:*Hermitian adjoint*Hermitian connection, the unique connection on a Hermitian manifold that satisfies specific conditions...
and
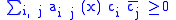
for every choice of complex numbers c1, ..., cn. This is proved using integration by parts
Integration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
.
These operators are elliptic
Elliptic operator
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
although in general elliptic operators may not be non-negative. They are however bounded from below.
Definition of Friedrichs extension
The definition of the Friedrichs extension is based on the theory of closed positive forms on Hilbert spaces.If T is non-negative, then
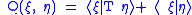
is a sesquilinear form on dom T and
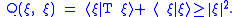
Thus Q defines an inner product on dom T. Let H1 be the completion
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
of dom T with respect to Q. H1 is an abstractly defined space; for instance its elements can be represented as equivalence classes of Cauchy sequence
Cauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
s of elements of dom T. It is not obvious that all elements in H1 can identified with elements of H. However, the following can be proved:
The canonical inclusion

extends to an injective continuous map H1 → H. We regard H1 as a subspace of H.
Define an operator A by
In the above formula, bounded is relative to the topology on H1 inherited from H. By the Riesz representation theorem
Riesz representation theorem
There are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
applied to the linear functional φξ extended to H, there is a unique A ξ ∈ H such that
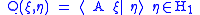
Theorem. A is a non-negative self-adjoint operator such that T1=A - I extends T.
T1 is the Friedrichs extension of T.
Krein's theorem on non-negative self-adjoint extensions
M. G. Krein has given an elegant characterization of all non-negative self-adjoint extensions of a non-negative symmetric operator T.If T, S are non-negative operators, write

if, and only if,
Theorem. There are unique self-adjoint extensions Tmin and Tmax of any non-negative symmetric operator T such that

and every non-negative self-adjoint extension S of T is between Tmin and Tmax, i.e

The Friedrichs extension of T is Tmax.