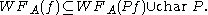FBI transform
Encyclopedia
In mathematics
, the FBI transform or Fourier–Bros–Iagolnitzer transform is a non-linear version of the Fourier transform
developed by the French mathematical physicists
Jacques Bros and Daniel Iagolnitzer in order to characterise the local analyticity
of functions (or distributions
) on Rn. The transform provides an alternative approach to analytic wave front set
s of distributions, developed independently by the Japanese mathematicians Mikio Sato
, Masaki Kashiwara
and Takahiro Kawai in their approach to microlocal analysis
. It can also be used to prove the analyticity of solutions of analytic elliptic partial differential equations as well as a version of the classical uniqueness theorem, strengthening the Cauchy–Kowalevski theorem, due to the Swedish mathematician Erik Holmgren (1873–1943).
of a Schwartz function f in S(Rn) is defined by
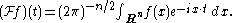
The FBI transform of f is defined for a ≥ 0 by
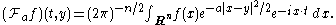
Thus, when a = 0, it essentially coincides with the Fourier transform.
The same formulas can be used to define the Fourier and FBI transforms of tempered distribution
s in
S(Rn).
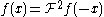
allows a function f to be recovered from its Fourier transform.
In particular
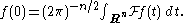
Similarly. at a positive value of a, f(0) can be recovered from the FBI transform of f(x) and xkf(x) by the inversion formula
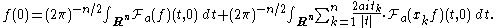
This formula can be proved by calculating the coefficients of am in the analytic function of a defined by the right hand side. These coefficients can be expressed in terms of the Fourier transform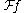 , the Euler operator
, the Euler operator
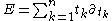
and the Laplacian operator

and easily computed using integration by parts
.
if and only if its FBI transform satisfies an inequality of the form
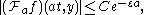
for a > 0, y near x and |t| sufficiently large, with C and ε positive constants.
and Mikio Sato
.
Theorem. Let P be an elliptic partial differential operator with analytic coefficients defined on an open subset
X of Rn. If Pf is analytic in X, then so too is f.
When "analytic" is replaced by "smooth" in this theorem, the result is just Hermann Weyl
's classical lemma on elliptic regularity, usually proved using Sobolev space
s (Warner 1983). It is a special case of more general results involing the analytic wave front set
(see below), which imply Holmgren's classical strengthening of the Cauchy–Kowalevski theorem on linear partial differential equation
s with real analytic coefficients. In modern language, Holmgren's uniquess theorem states that any distributional solution of such a system of equations must be analytic and therefore unique, by the Cauchy–Kowalevski theorem.
or singular spectrum WFA(f) of a distribution
f (or more generally of a hyperfunction
) can be defined in terms of the FBI transform as the complement of the conical set of points (x, λ·ξ) (λ > 0) such that the FBI transform satisfies the Bros–Iagolnitzer inequality

for all a > 0, y near x and t = λ·ξ, with |t| sufficiently large. J.M. Bony proved that this definition coincided with other definitions introduced independently by Sato, Kashiwara and Kawai and by Hörmander. If P is an mth order linear differential operator having analytic coefficients
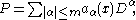
with principal symbol
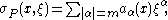
and characteristic variety
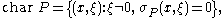
then
In particular, when P is elliptic, char P = ø, so that
This is a strengthening of the analytic version of elliptic regularity mentioned
above.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the FBI transform or Fourier–Bros–Iagolnitzer transform is a non-linear version of the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
developed by the French mathematical physicists
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
Jacques Bros and Daniel Iagolnitzer in order to characterise the local analyticity
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
of functions (or distributions
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
) on Rn. The transform provides an alternative approach to analytic wave front set
Wave front set
In mathematical analysis, more precisely in microlocal analysis, the wave front WF characterizes the singularities of a generalized function f, not only in space, but also with respect to its Fourier transform at each point...
s of distributions, developed independently by the Japanese mathematicians Mikio Sato
Mikio Sato
is a Japanese mathematician, who started the field of algebraic analysis. He studied at the University of Tokyo, and then did graduate study in physics as a student of Shin'ichiro Tomonaga...
, Masaki Kashiwara
Masaki Kashiwara
is a Japanese mathematician. He was a student of Mikio Sato at the University of Tokyo. Sato and Kashiwara have collaborated on algebraic analysis and D-module theory.He is a member of the French Academy of Sciences.- Concepts named after Kashiwara :...
and Takahiro Kawai in their approach to microlocal analysis
Microlocal analysis
In mathematical analysis, microlocal analysis comprises techniques developed from the 1950s onwards based on Fourier transforms related to the study of variable-coefficients-linear and nonlinear partial differential equations...
. It can also be used to prove the analyticity of solutions of analytic elliptic partial differential equations as well as a version of the classical uniqueness theorem, strengthening the Cauchy–Kowalevski theorem, due to the Swedish mathematician Erik Holmgren (1873–1943).
Definitions
The Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of a Schwartz function f in S(Rn) is defined by
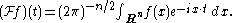
The FBI transform of f is defined for a ≥ 0 by
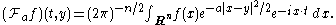
Thus, when a = 0, it essentially coincides with the Fourier transform.
The same formulas can be used to define the Fourier and FBI transforms of tempered distribution
Tempered distribution
*Distribution *Tempered representation...
s in
S(Rn).
Inversion formula
The Fourier inversion formula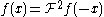
allows a function f to be recovered from its Fourier transform.
In particular
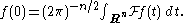
Similarly. at a positive value of a, f(0) can be recovered from the FBI transform of f(x) and xkf(x) by the inversion formula
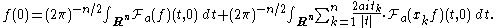
This formula can be proved by calculating the coefficients of am in the analytic function of a defined by the right hand side. These coefficients can be expressed in terms of the Fourier transform
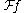 , the Euler operator
, the Euler operator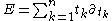
and the Laplacian operator

and easily computed using integration by parts
Integration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
.
Criterion for local analyticity
Bros and Iagolnitzer showed that a distribution f is locally equal to a real analytic function near xif and only if its FBI transform satisfies an inequality of the form
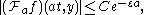
for a > 0, y near x and |t| sufficiently large, with C and ε positive constants.
Holmgren's uniqueness theorem
A simple consequence of the Bros and Iagolnitzer characterisation of local analyticity is the following regularity result of Lars HörmanderLars Hörmander
Lars Valter Hörmander is a Swedish mathematician who has been called "the foremost contributor to the modern theory of linear partial differential equations". He was awarded the Fields Medal in 1962, and the Wolf Prize in 1988...
and Mikio Sato
Mikio Sato
is a Japanese mathematician, who started the field of algebraic analysis. He studied at the University of Tokyo, and then did graduate study in physics as a student of Shin'ichiro Tomonaga...
.
Theorem. Let P be an elliptic partial differential operator with analytic coefficients defined on an open subset
X of Rn. If Pf is analytic in X, then so too is f.
When "analytic" is replaced by "smooth" in this theorem, the result is just Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
's classical lemma on elliptic regularity, usually proved using Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
s (Warner 1983). It is a special case of more general results involing the analytic wave front set
Wave front set
In mathematical analysis, more precisely in microlocal analysis, the wave front WF characterizes the singularities of a generalized function f, not only in space, but also with respect to its Fourier transform at each point...
(see below), which imply Holmgren's classical strengthening of the Cauchy–Kowalevski theorem on linear partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s with real analytic coefficients. In modern language, Holmgren's uniquess theorem states that any distributional solution of such a system of equations must be analytic and therefore unique, by the Cauchy–Kowalevski theorem.
The analytic wave front set
The analytic wave front setWave front set
In mathematical analysis, more precisely in microlocal analysis, the wave front WF characterizes the singularities of a generalized function f, not only in space, but also with respect to its Fourier transform at each point...
or singular spectrum WFA(f) of a distribution
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
f (or more generally of a hyperfunction
Hyperfunction
In mathematics, hyperfunctions are generalizations of functions, as a 'jump' from one holomorphic function to another at a boundary, and can be thought of informally as distributions of infinite order...
) can be defined in terms of the FBI transform as the complement of the conical set of points (x, λ·ξ) (λ > 0) such that the FBI transform satisfies the Bros–Iagolnitzer inequality

for all a > 0, y near x and t = λ·ξ, with |t| sufficiently large. J.M. Bony proved that this definition coincided with other definitions introduced independently by Sato, Kashiwara and Kawai and by Hörmander. If P is an mth order linear differential operator having analytic coefficients
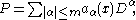
with principal symbol
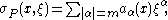
and characteristic variety
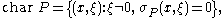
then
In particular, when P is elliptic, char P = ø, so that
- WFA(Pf) = WFA(f).
This is a strengthening of the analytic version of elliptic regularity mentioned
above.