
Enriques-Kodaira classification
Encyclopedia
In mathematics
, the Enriques–Kodaira classification is a classification of compact
complex surfaces into ten classes. For each of these classes, the surfaces in the class can be parametrized by a moduli space
. For most of the classes the moduli spaces are well understood, but for the class of surfaces of general type the moduli spaces seem too complicated to describe explicitly, though some components are known.
described the classification of complex projective surfaces. later extended the classification to include non-algebraic compact surfaces.
The analogous classification of surfaces in characteristic p > 0 was begun by and completed by ; it is similar to the characteristic projective 0 case, except there are a few extra types of surface in characteristics 2 and 3.
 The Enriques–Kodaira classification of compact complex surfaces states that every nonsingular minimal compact complex surface
The Enriques–Kodaira classification of compact complex surfaces states that every nonsingular minimal compact complex surface
is of exactly one of the 10 types listed on this page; in other words, it is one of the rational, ruled (genus >0), type VII, K3, Enriques, Kodaira, toric, hyperelliptic, properly quasi-elliptic, or general type surfaces.
For the 9 classes of surfaces other than general type, there is a fairly complete description of what all the surfaces look like (which for class VII depends on the global spherical shell conjecture, still unproved in 2009). For surfaces of general type not much is known about their explicit classification, though many examples have been found.
The classification of algebraic surfaces in positive characteristics is similar to that of algebraic surfaces in characteristic 0, except that there are no Kodaira surfaces or surfaces of type VII, and there are some extra families of Enriques surfaces in characteristic 2, and hyperelliptic surfaces in characteristics 2 and 3, and in Kodaira dimension 1 in characteristics 2 and 3 one also allows quasielliptic fibrations. These extra families can be understood as follows: In characteristic 0 these surfaces are the quotients of surfaces by finite groups, but in finite characteristics it is also possible to take quotients by finite group scheme
s that are not étale
.
Oscar Zariski
constructed some surfaces in positive characteristic that are unirational but not rational, derived from inseparable extensions (Zariski surface
s). Serre showed that h0(Ω) may differ from h1(O). Igusa showed that even when they are equal, they may be greater than the irregularity defined as the dimension of the Picard variety.
groups of coherent sheaves. The basic ones are the plurigenera and the Hodge numbers defined as follows:
By Serre duality
hi,j = h2−i,2−j, and h0,0 = h2,2 = 1. If the surface is Kähler
then hi,j = hj,i, so there are only 3 independent Hodge numbers.
For compact complex surfaces h1,0 is either h0,1 or h0,1 − 1.
The first plurigenus P1 is equal to the Hodge numbers h2,0 = h0,2,
and is sometimes called the geometric genus. The Hodge numbers of a complex surface depend only on the orientated real cohomology ring of the surface, and are invariant under birational transformations except for h1,1 which increases by 1 under blowing up a single point.
For complex surfaces the invariants above defined in terms of Hodge numbers depend only on the underlying oriented topological manifold.
NS(X) with rank the Picard number ρ, topological invariants such as the fundamental group
π1 and the integral homology and cohomology groups, and invariants of the underlying smooth 4-manifold
such as the Seiberg–Witten invariant
s and Donaldson invariants.
Given any point on a surface, we can form a new surface by blowing up
this point, which means roughly that we replace it by a copy of the projective line. A non-singular surface is called minimal if it cannot be obtained from another non-singular surface by blowing up a point, which is equivalent to saying it has no −1-curves (rational curves with self-intersection number −1). Every surface X is birational to a minimal non-singular surface, and this minimal non-singular surface is unique if X has Kodaira dimension at least 0 or is not algebraic. Algebraic surfaces of Kodaira dimension −∞ may be birational to more than 1 minimal non-singular surface, but it is easy to describe the relation between these minimal surfaces. For example, P1×P1 blown up at a point is isomorphic to P2 blown up twice. So to classify all compact complex surfaces up to birational isomorphism it is (more or less) enough to classify the minimal non-singular ones.
If q > 0 then the map to the Albanese variety has fibers that are projective lines (if the surface is minimal) so the surface is a ruled surface. If q = 0 this argument does not work as the Albanese variety is a point, but in this case Castelnovo's theorem
implies that the surface is rational.
For non-algebraic surfaces Kodaira found an extra class of surfaces, called type VII, which are still not well understood.
means surface birational to the complex projective plane P2. These are all algebraic. The minimal rational surfaces are P2 itself and the Hirzebruch surfaces Σn for n = 0 or n ≥ 2;. (The Hirzebruch surface Σn is the P1 bundle over P1 associated to the sheaf O(0)+O(n). The surface Σ0 is isomorphic to P1×P1, and Σ1 is isomorphic to P2 blown up at a point so is not minimal.)
Invariants: The plurigenera are all 0 and the fundamental group is trivial.
Hodge diamond:
Examples: P2, P1×P1 = Σ0, Hirzebruch surfaces Σn, quadric
s, cubic surface
s, del Pezzo surface
s, Veronese surface
. Many of these examples are non-minimal.
(The ones of genus 0 are the Hirzebruch surfaces and are rational.) Any ruled surface is birationally equivalent to P1×C for a unique curve C, so the classification of ruled surfaces up to birational equivalence is essentially the same as the classification of curves. A ruled surface not isomorphic to P1×P1 has a unique ruling (P1×P1 has two).
Invariants: The plurigenera are all 0.
Hodge diamond:
Examples: The product of any curve of genus > 0 with P1.
. The minimal ones with b2=0 have been classified by Bogomolov, and are either Hopf surface
s or Inoue surface
s. Examples with positive second Betti number include Inoue-Hirzebruch surfaces, Enoki surface
s, and more generally Kato surface
s. The global spherical shell conjecture implies that all minimal class VII surfaces with positive second Betti number are Kato surfaces, which would more or less complete the classification of the type VII surfaces.
Invariants: q=1, h1,0 = 0. All plurigenera are 0.
Hodge diamond:
Using χ= h0,0 − h0,1 + h0,2 and c2 = 2 − 2b1 + b2 gives
Moreover h0,2 is either 1 (if K = 0) or 0 (otherwise) as κ is 0. In general 2h0,1 ≥ b1, so three terms on the right are non-negative integers and there are only a few solutions to this equation.
For algebraic surfaces 2h0,1 − b1 is an even integer between 0 and 2pg, while for compact complex surfaces it is 0 or 1, and is 0 for Kähler surfaces
.
For Kähler surfaces
we have h1,0 = h0,1.
Most solutions to these conditions correspond to classes of surfaces, as in the following table:
s. All K3 surfaces are diffeomorphic, and their diffeomorphism class is an important example of a smooth spin simply connected 4-manifold.
Invariants: The second cohomology group H2(X, Z) is isomorphic to the unique even unimodular lattice
II3,19 of dimension 22 and signature −16.
Hodge diamond:
Examples:
A marked K3 surface is a K3 surface together with an isomorphism from II3,19 to H2(X, Z).
The moduli space of marked K3 surfaces is connected non-Hausdorff smooth analytic space of dimension 20. The algebraic K3 surfaces form a countable collection of 19-dimensional subvarieties of it.
s. One dimensional complex tori are just elliptic curves and are all algebraic, but Riemann discovered that most complex tori of dimension 2 are not algebraic. The algebraic ones are exactly the 2-dimensional abelian varieties
.
Most of their theory is a special case of the theory of higher-dimensional tori or abelian varieties. Criteria to be a product of two elliptic curves (up to isogeny
) were a popular study in the nineteenth century.
Invariants: The plurigenera are all 1. The surface is diffeomorphic to S1×S1×S1×S1 so the fundamental group is Z4.
Hodge diamond:
Examples: A product of two elliptic curves. The Jacobian of a genus 2 curve. Any quotient of C4 by a lattice.
Invariants: If the surface is the quotient of a primary Kodaira surface by a group of order k=1,2,3,4,6, then the plurigenera Pn are 1 if n is divisible by k and 0 otherwise.
Hodge diamond:
Examples: Take a non-trivial line bundle over an elliptic curve, remove the zero section, then quotient out the fibers by Z acting as multiplication by powers of some complex number z.
This gives a primary Kodaira surface.
). They are quotients of K3 surfaces by a group of order 2 and their theory is similar to that of algebraic K3 surfaces.
Invariants: The plurigenera Pn are 1 if n is even and 0 if n is odd. The fundamental group has order 2. The second cohomology group H2(X, Z) is isomorphic to the sum of the unique even unimodular lattice
II1,9 of dimension 10 and signature -8 and a group of order 2.
Hodge diamond:
Marked Enriques surfaces form a connected 10-dimensional family, which has been described explicitly.
In characteristic 2 there are some extra families of Enriques surfaces called singular and supersingular Enriques surfaces; see the article on Enriques surface
s for details.
Z/4Z, Z/4Z+Z/2Z, or Z/6Z, giving 7 families of such surfaces. Over fields of characteristics 2 or 3 there are some extra families given by taking quotients by a non-etale group scheme; see the article on
hyperelliptic surface
s for details.
Hodge diamond:
is a surface equipped with an elliptic fibration (a surjective holomorphic map to a curve B such that all but finitely many fibers are smooth irreducible curves of genus 1). The generic fiber in such a fibration is a genus 1 curve over the function field of B. Conversely, given a genus 1 curve over the function field of a curve, its relative minimal model is an elliptic surface. Kodaira and others have given a fairly complete description of all elliptic surfaces. In particular, Kodaira gave a complete list of the possible singular fibers. The theory of elliptic surfaces is analogous to the theory of proper regular models of elliptic curves over discrete valuation ring
s (e.g., the ring of p-adic integers) and Dedekind domain
s (e.g., the ring of integers of a number field).
In finite characteristic 2 and 3 one can also get quasi-elliptic surfaces, whose fibers may almost all be rational curves with a single node, which are "degenerate elliptic curves".
Every surface of Kodaira dimension
1 is an elliptic surface (or a quasielliptic surface in characteristics 2 or 3),
but the converse is not true: an elliptic surface can have Kodaira dimension −∞, 0, or 1.
All Enriques surface
s, all hyperelliptic surface
s, all Kodaira surface
s, some K3 surface
s, some abelian surface
s, and some rational surface
s are elliptic surfaces, and these examples have Kodaira dimension less than 1.
An elliptic surface whose base curve B is of genus at least 2 always has Kodaira dimension 1, but the Kodaira dimension can be 1 also for some elliptic surfaces with B of genus 0 or 1.
Invariants: c12 = 0, c2≥ 0.
Example: If E is an elliptic curve and B is a curve of genus at least 2, then E×B is an elliptic surface of Kodaira dimension 1.
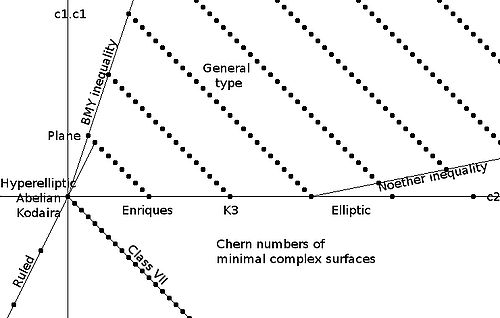
Invariants: There are several conditions that the Chern numbers of a minimal complex surface of general type must satisfy:
Most pairs of integers satisfying these conditions are the Chern numbers for some complex surface of general type.
Examples: The simplest examples are the product of two curves of genus at least 2, and a hypersurface of degree at least 5 in P3. There are a large number of other constructions known. However there is no
known construction that can produce "typical" surfaces of general type for large Chern numbers; in fact it is not even known if there is any reasonable concept of a "typical" surface of general type. There are many other examples that have been found, including most Hilbert modular surface
s, fake projective plane
s, Barlow surface
s, and so on.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Enriques–Kodaira classification is a classification of compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
complex surfaces into ten classes. For each of these classes, the surfaces in the class can be parametrized by a moduli space
Moduli space
In algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
. For most of the classes the moduli spaces are well understood, but for the class of surfaces of general type the moduli spaces seem too complicated to describe explicitly, though some components are known.
described the classification of complex projective surfaces. later extended the classification to include non-algebraic compact surfaces.
The analogous classification of surfaces in characteristic p > 0 was begun by and completed by ; it is similar to the characteristic projective 0 case, except there are a few extra types of surface in characteristics 2 and 3.
Statement of the classification

is of exactly one of the 10 types listed on this page; in other words, it is one of the rational, ruled (genus >0), type VII, K3, Enriques, Kodaira, toric, hyperelliptic, properly quasi-elliptic, or general type surfaces.
For the 9 classes of surfaces other than general type, there is a fairly complete description of what all the surfaces look like (which for class VII depends on the global spherical shell conjecture, still unproved in 2009). For surfaces of general type not much is known about their explicit classification, though many examples have been found.
The classification of algebraic surfaces in positive characteristics is similar to that of algebraic surfaces in characteristic 0, except that there are no Kodaira surfaces or surfaces of type VII, and there are some extra families of Enriques surfaces in characteristic 2, and hyperelliptic surfaces in characteristics 2 and 3, and in Kodaira dimension 1 in characteristics 2 and 3 one also allows quasielliptic fibrations. These extra families can be understood as follows: In characteristic 0 these surfaces are the quotients of surfaces by finite groups, but in finite characteristics it is also possible to take quotients by finite group scheme
Group scheme
In mathematics, a group scheme is a type of algebro-geometric object equipped with a composition law. Group schemes arise naturally as symmetries of schemes, and they generalize algebraic groups, in the sense that all algebraic groups have group scheme structure, but group schemes are not...
s that are not étale
Étale
In mathematics, more specifically in algebra, the adjective étale refers to several closely related concepts:* Étale morphism** Formally étale morphism* Étale cohomology* Étale topology* Étale fundamental group* Étale space* Étale group scheme...
.
Oscar Zariski
Oscar Zariski
Oscar Zariski was a Russian mathematician and one of the most influential algebraic geometers of the 20th century.-Education:...
constructed some surfaces in positive characteristic that are unirational but not rational, derived from inseparable extensions (Zariski surface
Zariski surface
In algebraic geometry, a branch of mathematics, a Zariski surface is a surface over a field of characteristic p > 0 such that there is a dominant inseparable map of degree p from the projective plane to the surface...
s). Serre showed that h0(Ω) may differ from h1(O). Igusa showed that even when they are equal, they may be greater than the irregularity defined as the dimension of the Picard variety.
Hodge numbers and Kodaira dimension
The most important invariants of a compact complex surfaces used in the classification can be given in terms of the dimensions of various cohomologySheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
groups of coherent sheaves. The basic ones are the plurigenera and the Hodge numbers defined as follows:
- K is the canonical line bundle whose sections are the holomorphic 2-forms.
- Pn = dim H0(Kn) for n ≥ 1 are the plurigenera. They are birational invariants, i.e. invariant under blowing up. Using Seiberg–Witten theory Friedman and Morgan showed that for complex manifolds they only depend on the underlying oriented smooth 4-manifold. For non-Kähler surfaces the plurigenera are determined by the fundamental group, but for Kähler surfacesKähler manifoldIn mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
there are examples of surfaces that are homeomorphic but have different plurigenera and Kodaira dimensions. The individual plurigenera are not often used; the most important thing about them is their growth rate, measured by the Kodaira dimensionKodaira dimensionIn algebraic geometry, the Kodaira dimension κ measures the size of the canonical model of a projective variety V.The definition of Kodaira dimension, named for Kunihiko Kodaira, and the notation κ were introduced in the seminar.-The plurigenera:...
:
- κ is the Kodaira dimensionKodaira dimensionIn algebraic geometry, the Kodaira dimension κ measures the size of the canonical model of a projective variety V.The definition of Kodaira dimension, named for Kunihiko Kodaira, and the notation κ were introduced in the seminar.-The plurigenera:...
: it is −∞ (sometimes written −1) if the plurigenera are all 0, and is otherwise the smallest number (0, 1, or 2 for surfaces) such that Pn/nκ is bounded. Enriques did not use this definition: instead he used the values of P12 and K.K = c12. These determine the Kodaira dimension, since Kodaira dimension κ = −∞ corresponds to P12 = 0, κ = 0 corresponds to P12 = 1, κ = 1 corresponds to P12 > 1 and K.K = 0, while κ = 2 corresponds to P12 > 1 and K.K > 0.
- hi,j = dim Hj(X, Ωi), where Ωi is the sheaf of holomorphic i-forms, are the Hodge numbers, often arranged in the Hodge diamond:
| h0,0 | ||||
|---|---|---|---|---|
| h1,0 | h0,1 | |||
| h2,0 | h1,1 | h0,2 | ||
| h2,1 | h1,2 | |||
| h2,2 |
By Serre duality
Serre duality
In algebraic geometry, a branch of mathematics, Serre duality is a duality present on non-singular projective algebraic varieties V of dimension n . It shows that a cohomology group Hi is the dual space of another one, Hn−i...
hi,j = h2−i,2−j, and h0,0 = h2,2 = 1. If the surface is Kähler
Kähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
then hi,j = hj,i, so there are only 3 independent Hodge numbers.
For compact complex surfaces h1,0 is either h0,1 or h0,1 − 1.
The first plurigenus P1 is equal to the Hodge numbers h2,0 = h0,2,
and is sometimes called the geometric genus. The Hodge numbers of a complex surface depend only on the orientated real cohomology ring of the surface, and are invariant under birational transformations except for h1,1 which increases by 1 under blowing up a single point.
Invariants related to Hodge numbers
There are many invariants that (at least for complex surfaces) can be written as linear combinations of the Hodge numbers, as follows:- b0,b1,b2,b3,b4 are the Betti numberBetti numberIn algebraic topology, a mathematical discipline, the Betti numbers can be used to distinguish topological spaces. Intuitively, the first Betti number of a space counts the maximum number of cuts that can be made without dividing the space into two pieces....
s: bi = dim(Hi(S)). b0 = b4 = 1 and b1 = b3 = h1,0 + h0,1 = h2,1 + h1,2 and b2 = h2,0 + h1,1 + h0,2. In characteristic p > 0 the Betti numbers (defined using l-adic cohomomology) need not be related in this way to Hodge numbers.
- e = b0 − b1 + b2 − b3 + b4 is the Euler characteristicEuler characteristicIn mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
or Euler number.
- q is the irregularityIrregularity of a surfaceIn mathematics, the irregularity of a complex surface X is the Hodge number h0,1= dim H1, usually denoted by q . The irregularity of an algebraic surface is sometimes defined to be this Hodge number, and sometimes defined to be the dimension of the Picard variety , which is the same in...
, the dimension of the Picard variety and the Albanese varietyAlbanese varietyIn mathematics, the Albanese variety A, named for Giacomo Albanese, is a generalization of the Jacobian variety of a curve, and is the abelian variety generated by a variety V. In other words there is a morphism from the variety V to its Albanese variety A, such that any morphism from V to an...
, which for complex surfaces (but not always for surfaces of prime characteristic) is h0,1.
- pg = h0,2 = h2,0 = P1is the geometric genusGeometric genusIn algebraic geometry, the geometric genus is a basic birational invariant pg of algebraic varieties and complex manifolds.-Definition:...
.
- pa = pg − q = h0,2 − h0,1 is the arithmetic genusArithmetic genusIn mathematics, the arithmetic genus of an algebraic variety is one of some possible generalizations of the genus of an algebraic curve or Riemann surface.The arithmetic genus of a projective complex manifold...
.
- χ = pg − q + 1 = h0,2 − h0,1 + 1 is the holomorphic Euler characteristic of the trivial bundle. (It usually differs from the Euler number e defined above.) By Noether's formula it is also equal to the Todd genus (c12 + c2)/12
- τ is the signature (of the second cohomology group for complex surfaces) and is equal to 4χ−e, which is Σi,j(−1)jhi,j.
- b+ and b− are the dimensions of the maximal positive and negative definite subspaces of H2, so b+ + b − = b2 and b+ − b− = τ.
- c2 = e and c12 = K2 = 12χ − e are the Chern numbers, defined as the integrals of various polynomials in the Chern classChern classIn mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
es over the manifold.
For complex surfaces the invariants above defined in terms of Hodge numbers depend only on the underlying oriented topological manifold.
Other invariants
There are further invariants of compact complex surfaces that are not used so much in the classification. These include algebraic invariants such as the Picard group Pic(X) of divisors modulo linear equivalence, its quotient the Néron–Severi groupNéron–Severi group
In algebraic geometry, the Néron–Severi group of a variety isthe group of divisors modulo algebraic equivalence; in other words it is the group of components of the Picard scheme of a variety. Its rank is called the Picard number...
NS(X) with rank the Picard number ρ, topological invariants such as the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
π1 and the integral homology and cohomology groups, and invariants of the underlying smooth 4-manifold
4-manifold
In mathematics, 4-manifold is a 4-dimensional topological manifold. A smooth 4-manifold is a 4-manifold with a smooth structure. In dimension four, in marked contrast with lower dimensions, topological and smooth manifolds are quite different...
such as the Seiberg–Witten invariant
Seiberg–Witten invariant
In mathematics, Seiberg–Witten invariants are invariants of compact smooth 4-manifolds introduced by , using the Seiberg–Witten theory studied by during their investigations of Seiberg–Witten gauge theory....
s and Donaldson invariants.
Minimal models and blowing up
Any surface is birational to a non-singular surface, so for most purposes it is enough to classify the non-singular surfaces.Given any point on a surface, we can form a new surface by blowing up
Blowing up
In mathematics, blowing up or blowup is a type of geometric transformation which replaces a subspace of a given space with all the directions pointing out of that subspace. For example, the blowup of a point in a plane replaces the point with the projectivized tangent space at that point...
this point, which means roughly that we replace it by a copy of the projective line. A non-singular surface is called minimal if it cannot be obtained from another non-singular surface by blowing up a point, which is equivalent to saying it has no −1-curves (rational curves with self-intersection number −1). Every surface X is birational to a minimal non-singular surface, and this minimal non-singular surface is unique if X has Kodaira dimension at least 0 or is not algebraic. Algebraic surfaces of Kodaira dimension −∞ may be birational to more than 1 minimal non-singular surface, but it is easy to describe the relation between these minimal surfaces. For example, P1×P1 blown up at a point is isomorphic to P2 blown up twice. So to classify all compact complex surfaces up to birational isomorphism it is (more or less) enough to classify the minimal non-singular ones.
Surfaces of Kodaira dimension −∞
Algebraic surfaces of Kodaira dimension −∞ can be classified as follows.If q > 0 then the map to the Albanese variety has fibers that are projective lines (if the surface is minimal) so the surface is a ruled surface. If q = 0 this argument does not work as the Albanese variety is a point, but in this case Castelnovo's theorem
Rational surface
In algebraic geometry, a branch of mathematics, a rational surface is a surface birationally equivalent to the projective plane, or in other words a rational variety of dimension two...
implies that the surface is rational.
For non-algebraic surfaces Kodaira found an extra class of surfaces, called type VII, which are still not well understood.
Rational surfaces
Rational surfaceRational surface
In algebraic geometry, a branch of mathematics, a rational surface is a surface birationally equivalent to the projective plane, or in other words a rational variety of dimension two...
means surface birational to the complex projective plane P2. These are all algebraic. The minimal rational surfaces are P2 itself and the Hirzebruch surfaces Σn for n = 0 or n ≥ 2;. (The Hirzebruch surface Σn is the P1 bundle over P1 associated to the sheaf O(0)+O(n). The surface Σ0 is isomorphic to P1×P1, and Σ1 is isomorphic to P2 blown up at a point so is not minimal.)
Invariants: The plurigenera are all 0 and the fundamental group is trivial.
Hodge diamond:
| 1 | |||||
|---|---|---|---|---|---|
| 0 | 0 | ||||
| 0 | 1 | 0 | (Projective plane) | ||
| 0 | 0 | ||||
| 1 |
| 1 | |||||
|---|---|---|---|---|---|
| 0 | 0 | ||||
| 0 | 2 | 0 | (Hirzebruch surfaces) | ||
| 0 | 0 | ||||
| 1 |
Examples: P2, P1×P1 = Σ0, Hirzebruch surfaces Σn, quadric
Quadric
In mathematics, a quadric, or quadric surface, is any D-dimensional hypersurface in -dimensional space defined as the locus of zeros of a quadratic polynomial...
s, cubic surface
Cubic surface
A cubic surface is a projective variety studied in algebraic geometry. It is an algebraic surface in three-dimensional projective space defined by a single polynomial which is homogeneous of degree 3...
s, del Pezzo surface
Del Pezzo surface
In mathematics, a del Pezzo surface or Fano surface is a two-dimensional Fano variety, in other words a non-singular projective algebraic surface with ample anticanonical divisor class...
s, Veronese surface
Veronese surface
In mathematics, the Veronese surface is an algebraic surface in five-dimensional projective space, and is realized by the Veronese embedding, the embedding of the projective plane given by the complete linear system of conics. It is named after Giuseppe Veronese...
. Many of these examples are non-minimal.
Ruled surfaces of genus > 0
Ruled surfaces of genus g have a smooth morphism to a curve of genus g whose fibers are lines P1. They are all algebraic.(The ones of genus 0 are the Hirzebruch surfaces and are rational.) Any ruled surface is birationally equivalent to P1×C for a unique curve C, so the classification of ruled surfaces up to birational equivalence is essentially the same as the classification of curves. A ruled surface not isomorphic to P1×P1 has a unique ruling (P1×P1 has two).
Invariants: The plurigenera are all 0.
Hodge diamond:
| 1 | ||||
|---|---|---|---|---|
| g | g | |||
| 0 | 2 | 0 | ||
| g | g | |||
| 1 |
Examples: The product of any curve of genus > 0 with P1.
Surfaces of class VII
These surfaces are never algebraic or KählerKähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
. The minimal ones with b2=0 have been classified by Bogomolov, and are either Hopf surface
Hopf surface
In complex geometry, a Hopf surface is a compact complex surface obtainedas a quotient of the complex vector space C2 \ 0...
s or Inoue surface
Inoue surface
In complex geometry, a part of mathematics, the termInoue surface denotes several complex surfacesof Kodaira class VII. They arenamed after Masahisa Inoue, who gave the first non-trivialexamples of Kodaira class VII surfaces in 1974....
s. Examples with positive second Betti number include Inoue-Hirzebruch surfaces, Enoki surface
Enoki surface
In mathematics, an Enoki surface is compact complex surface with positive second Betti number that has a global spherical shell and a non-trivial divisor D with H0 ≠ 0 and = 0. constructed some examples. They are surfaces of class VII, so are non-Kähler and have Kodaira...
s, and more generally Kato surface
Kato surface
In mathematics, a Kato surface is a compact complex surface with positive first Betti number that has a global spherical shell. showed that Kato surfaces have small analytic deformations that are the blowups of primary Hopf surfaces at a finite number of points. In particular they have an infinite...
s. The global spherical shell conjecture implies that all minimal class VII surfaces with positive second Betti number are Kato surfaces, which would more or less complete the classification of the type VII surfaces.
Invariants: q=1, h1,0 = 0. All plurigenera are 0.
Hodge diamond:
| 1 | ||||
|---|---|---|---|---|
| 0 | 1 | |||
| 0 | b2 | 0 | ||
| 1 | 0 | |||
| 1 |
Surfaces of Kodaira dimension 0
These surfaces are classified by starting with Noether's formula 12χ=c2 + c12. For Kodaira dimension 0, K has zero intersection number with itself, so c12 = 0.Using χ= h0,0 − h0,1 + h0,2 and c2 = 2 − 2b1 + b2 gives
- 10 + 12h0,2 = 8h0,1 + 2(2h0,1 − b1) +b2.
Moreover h0,2 is either 1 (if K = 0) or 0 (otherwise) as κ is 0. In general 2h0,1 ≥ b1, so three terms on the right are non-negative integers and there are only a few solutions to this equation.
For algebraic surfaces 2h0,1 − b1 is an even integer between 0 and 2pg, while for compact complex surfaces it is 0 or 1, and is 0 for Kähler surfaces
Kähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
.
For Kähler surfaces
Kähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
we have h1,0 = h0,1.
Most solutions to these conditions correspond to classes of surfaces, as in the following table:
| b2 | b1 | h0,1 | pg =h0,2 | h1,0 | h1,1 | Surfaces | Fields |
|---|---|---|---|---|---|---|---|
| 22 | 0 | 0 | 1 | 0 | 20 | K3 | Any. Always Kähler Kähler manifold In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the... over the complex numbers, but need not be algebraic. |
| 10 | 0 | 0 | 0 | 0 | 10 | Classical Enriques | Any. Always algebraic. |
| 10 | 0 | 1 | 1 | Non-classical Enriques | Only characteristic 2 | ||
| 6 | 4 | 2 | 1 | 2 | 4 | Abelian surfaces, tori | Any. Always Kähler Kähler manifold In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the... over the complex numbers, but need not be algebraic. |
| 2 | 2 | 1 | 0 | 1 | 2 | Hyperelliptic | Any. Always algebraic |
| 2 | 2 | 2 | 1 | Quasi-hyperelliptic | Only characteristics 2, 3 | ||
| 4 | 3 | 2 | 1 | 1 | 2 | Primary Kodaira | Only complex, never Kähler Kähler manifold In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the... |
| 0 | 1 | 1 | 0 | 0 | 0 | Secondary Kodaira | Only complex, never Kähler Kähler manifold In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the... |
K3 surfaces
These are the minimal compact complex surfaces of Kodaira dimension 0 with q = 0 and trivial canonical line bundle. They are all Kähler manifoldKähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
s. All K3 surfaces are diffeomorphic, and their diffeomorphism class is an important example of a smooth spin simply connected 4-manifold.
Invariants: The second cohomology group H2(X, Z) is isomorphic to the unique even unimodular lattice
Unimodular lattice
In mathematics, a unimodular lattice is a lattice of determinant 1 or −1.The E8 lattice and the Leech lattice are two famous examples.- Definitions :...
II3,19 of dimension 22 and signature −16.
Hodge diamond:
| 1 | ||||
|---|---|---|---|---|
| 0 | 0 | |||
| 1 | 20 | 1 | ||
| 0 | 0 | |||
| 1 |
Examples:
- Degree 4 hypersurfaces in P3(C)
- Kummer surfaces. These are obtained by quotienting out an abelian surface by the automorphism a → −a, then blowing up the 16 singular points.
A marked K3 surface is a K3 surface together with an isomorphism from II3,19 to H2(X, Z).
The moduli space of marked K3 surfaces is connected non-Hausdorff smooth analytic space of dimension 20. The algebraic K3 surfaces form a countable collection of 19-dimensional subvarieties of it.
Abelian surfaces and 2-dimensional complex tori
The two-dimensional complex tori include the abelian surfaceAbelian surface
In mathematics, an abelian surface is 2-dimensional abelian variety.One dimensional complex tori are just elliptic curves and are all algebraic, but Riemann discovered that most complex tori of dimension 2 are not algebraic...
s. One dimensional complex tori are just elliptic curves and are all algebraic, but Riemann discovered that most complex tori of dimension 2 are not algebraic. The algebraic ones are exactly the 2-dimensional abelian varieties
Abelian variety
In mathematics, particularly in algebraic geometry, complex analysis and number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions...
.
Most of their theory is a special case of the theory of higher-dimensional tori or abelian varieties. Criteria to be a product of two elliptic curves (up to isogeny
Isogeny
In mathematics, an isogeny is a morphism of varieties between two abelian varieties that is surjective and has a finite kernel....
) were a popular study in the nineteenth century.
Invariants: The plurigenera are all 1. The surface is diffeomorphic to S1×S1×S1×S1 so the fundamental group is Z4.
Hodge diamond:
| 1 | ||||
|---|---|---|---|---|
| 2 | 2 | |||
| 1 | 4 | 1 | ||
| 2 | 2 | |||
| 1 |
Examples: A product of two elliptic curves. The Jacobian of a genus 2 curve. Any quotient of C4 by a lattice.
Kodaira surfaces
These are never algebraic, though they have non-constant meromorphic functions. They are usually divided into two subtypes: primary Kodaira surfaces with trivial canonical bundle, and secondary Kodaira surfaces which are quotients of these by finite groups of orders 2, 3, 4, or 6, and which have non-trivial canonical bundles. The secondary Kodaira surfaces have the same relation to primary ones that Enriques surfaces have to K3 surfaces, or bielliptic surfaces have to abelian surfaces.Invariants: If the surface is the quotient of a primary Kodaira surface by a group of order k=1,2,3,4,6, then the plurigenera Pn are 1 if n is divisible by k and 0 otherwise.
Hodge diamond:
| 1 | |||||
|---|---|---|---|---|---|
| 1 | 2 | ||||
| 1 | 2 | 1 | (Primary) | ||
| 2 | 1 | ||||
| 1 |
| 1 | |||||
|---|---|---|---|---|---|
| 0 | 1 | ||||
| 0 | 0 | 0 | (Secondary) | ||
| 1 | 0 | ||||
| 1 |
Examples: Take a non-trivial line bundle over an elliptic curve, remove the zero section, then quotient out the fibers by Z acting as multiplication by powers of some complex number z.
This gives a primary Kodaira surface.
Enriques surfaces
These are the complex surfaces such that q = 0 and the canonical line bundle is non-trivial, but has trivial square. Enriques surfaces are all algebraic (and therefore KählerKähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
). They are quotients of K3 surfaces by a group of order 2 and their theory is similar to that of algebraic K3 surfaces.
Invariants: The plurigenera Pn are 1 if n is even and 0 if n is odd. The fundamental group has order 2. The second cohomology group H2(X, Z) is isomorphic to the sum of the unique even unimodular lattice
Unimodular lattice
In mathematics, a unimodular lattice is a lattice of determinant 1 or −1.The E8 lattice and the Leech lattice are two famous examples.- Definitions :...
II1,9 of dimension 10 and signature -8 and a group of order 2.
Hodge diamond:
| 1 | ||||
|---|---|---|---|---|
| 0 | 0 | |||
| 0 | 10 | 0 | ||
| 0 | 0 | |||
| 1 |
Marked Enriques surfaces form a connected 10-dimensional family, which has been described explicitly.
In characteristic 2 there are some extra families of Enriques surfaces called singular and supersingular Enriques surfaces; see the article on Enriques surface
Enriques surface
In mathematics, Enriques surfaces, discovered by , are complex algebraic surfacessuch that the irregularity q = 0 and the canonical line bundle K is non-trivial but has trivial square...
s for details.
Hyperelliptic (or bielliptic) surfaces
Over the complex numbers these are quotients of a product of two elliptic curves by a finite group of automorphisms. The finite group can be Z/2Z, Z/2Z+Z/2Z, Z/3Z, Z/3Z+Z/3Z,Z/4Z, Z/4Z+Z/2Z, or Z/6Z, giving 7 families of such surfaces. Over fields of characteristics 2 or 3 there are some extra families given by taking quotients by a non-etale group scheme; see the article on
hyperelliptic surface
Hyperelliptic surface
In mathematics, a hyperelliptic surface, or bi-elliptic surface, is a surface with an elliptic fibration over an elliptic curve. Any such surface can be written as the quotient of a product of two elliptic curves by a finite abelian group....
s for details.
Hodge diamond:
| 1 | ||||
|---|---|---|---|---|
| 1 | 1 | |||
| 0 | 2 | 0 | ||
| 1 | 1 | |||
| 1 |
Surfaces of Kodaira dimension 1
An elliptic surfaceElliptic surface
In mathematics, an elliptic surface is a surface that has an elliptic fibration, in other words a proper connected morphism to an algebraic curve, almost all of whose fibers are elliptic curves....
is a surface equipped with an elliptic fibration (a surjective holomorphic map to a curve B such that all but finitely many fibers are smooth irreducible curves of genus 1). The generic fiber in such a fibration is a genus 1 curve over the function field of B. Conversely, given a genus 1 curve over the function field of a curve, its relative minimal model is an elliptic surface. Kodaira and others have given a fairly complete description of all elliptic surfaces. In particular, Kodaira gave a complete list of the possible singular fibers. The theory of elliptic surfaces is analogous to the theory of proper regular models of elliptic curves over discrete valuation ring
Discrete valuation ring
In abstract algebra, a discrete valuation ring is a principal ideal domain with exactly one non-zero maximal ideal.This means a DVR is an integral domain R which satisfies any one of the following equivalent conditions:...
s (e.g., the ring of p-adic integers) and Dedekind domain
Dedekind domain
In abstract algebra, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily unique up to the order of the factors...
s (e.g., the ring of integers of a number field).
In finite characteristic 2 and 3 one can also get quasi-elliptic surfaces, whose fibers may almost all be rational curves with a single node, which are "degenerate elliptic curves".
Every surface of Kodaira dimension
Kodaira dimension
In algebraic geometry, the Kodaira dimension κ measures the size of the canonical model of a projective variety V.The definition of Kodaira dimension, named for Kunihiko Kodaira, and the notation κ were introduced in the seminar.-The plurigenera:...
1 is an elliptic surface (or a quasielliptic surface in characteristics 2 or 3),
but the converse is not true: an elliptic surface can have Kodaira dimension −∞, 0, or 1.
All Enriques surface
Enriques surface
In mathematics, Enriques surfaces, discovered by , are complex algebraic surfacessuch that the irregularity q = 0 and the canonical line bundle K is non-trivial but has trivial square...
s, all hyperelliptic surface
Hyperelliptic surface
In mathematics, a hyperelliptic surface, or bi-elliptic surface, is a surface with an elliptic fibration over an elliptic curve. Any such surface can be written as the quotient of a product of two elliptic curves by a finite abelian group....
s, all Kodaira surface
Kodaira surface
In mathematics, a Kodaira surface is a compact complex surface of Kodaira dimension 0 and odd first Betti number.These are never algebraic, though they have non-constant meromorphic functions...
s, some K3 surface
K3 surface
In mathematics, a K3 surface is a complex or algebraic smooth minimal complete surface that is regular and has trivial canonical bundle.In the Enriques-Kodaira classification of surfaces they form one of the 5 classes of surfaces of Kodaira dimension 0....
s, some abelian surface
Abelian surface
In mathematics, an abelian surface is 2-dimensional abelian variety.One dimensional complex tori are just elliptic curves and are all algebraic, but Riemann discovered that most complex tori of dimension 2 are not algebraic...
s, and some rational surface
Rational surface
In algebraic geometry, a branch of mathematics, a rational surface is a surface birationally equivalent to the projective plane, or in other words a rational variety of dimension two...
s are elliptic surfaces, and these examples have Kodaira dimension less than 1.
An elliptic surface whose base curve B is of genus at least 2 always has Kodaira dimension 1, but the Kodaira dimension can be 1 also for some elliptic surfaces with B of genus 0 or 1.
Invariants: c12 = 0, c2≥ 0.
Example: If E is an elliptic curve and B is a curve of genus at least 2, then E×B is an elliptic surface of Kodaira dimension 1.
Surfaces of Kodaira dimension 2 (surfaces of general type)
These are all algebraic, and in some sense most surfaces are in this class. Gieseker showed that there is a coarse moduli scheme for surfaces of general type; this means that for any fixed values of the Chern numbers c12 and c2, there is a quasi-projective scheme classifying the surfaces of general type with those Chern numbers. However it is a very difficult problem to describe these schemes explicitly, and there are very few pairs of Chern numbers for which this has been done (except when the scheme is empty!)Invariants: There are several conditions that the Chern numbers of a minimal complex surface of general type must satisfy:
- c12 > 0, c2 > 0
- c12 ≤ 3c2 (the Bogomolov–Miyaoka–Yau inequalityBogomolov–Miyaoka–Yau inequalityIn mathematics, the Bogomolov–Miyaoka–Yau inequality is the inequality c_1^2 \le 3 c_2\ between Chern numbers of compact complex surfaces of general type. Its major interest is the way it restricts the possible topological types of the underlying real 4-manifold...
) - 5c12 − c2 + 36 ≥ 0 (the Noether inequality)
- c12 + c2 is divisible by 12.
Most pairs of integers satisfying these conditions are the Chern numbers for some complex surface of general type.
Examples: The simplest examples are the product of two curves of genus at least 2, and a hypersurface of degree at least 5 in P3. There are a large number of other constructions known. However there is no
known construction that can produce "typical" surfaces of general type for large Chern numbers; in fact it is not even known if there is any reasonable concept of a "typical" surface of general type. There are many other examples that have been found, including most Hilbert modular surface
Hilbert modular surface
In mathematics, a Hilbert modular surface is one of the surfaces obtained by taking a quotient of a product of two copies of the upper half-plane by a Hilbert modular group....
s, fake projective plane
Fake projective plane
In mathematics, a fake projective plane is one of the 50 complex algebraic surfaces that have the same Betti numbers as the projective plane, but are not isomorphic to it. Such objects are always algebraic surfaces of general type....
s, Barlow surface
Barlow surface
In mathematics, a Barlow surface is one of the complex surfaces introduced by .They are simply connected surfaces of general type with pg = 0. They are homeomorphic but not diffeomorphic to a projective plane blown up in 8 points....
s, and so on.

