Kodaira dimension
Encyclopedia
In algebraic geometry
, the Kodaira dimension κ(V) measures the size of the canonical model
of a projective variety V.
The definition of Kodaira dimension, named for Kunihiko Kodaira, and the notation κ were introduced in the seminar
.
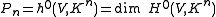
is the classically-defined n-th plurigenus of V.
The pluricanonical divisor
, via the corresponding linear system of divisors
, gives a map to projective space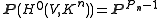
,
called the n-canonical map.
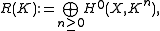
where K is a canonical divisor of V. The projective dimension of R(K) is called the Kodaira dimension.
Conventionally, when R is trivial (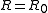
= underlying field (constant functions); the plurigenera are all zero (other than 
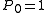); the pluricanonical divisors are not effective), which happens for example when V is rational, one takes 
(in agreement with the transcendence degree definition), or sometimes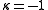 
(which is a conventional dimension of the empty set, as it preserves additivity under multiplication).
Kodaira dimensions can take any value from −1 to the dimension
of V.
Varieties with low Kodaira dimension are special, while varieties of maximal Kodaira dimension are (suggestively) called general type.
Geometrically, there is a rough correspondence between Kodaira dimension and curvature: negative Kodaira dimension corresponds to positive curvature, zero Kodaira dimension corresponds to flatness, and maximum Kodaira dimension (general type) corresponds to negative curvature.
The specialness of varieties of low Kodaira dimension corresponds to the specialness of Riemannian manifolds of positive curvature (and general type corresponds to the genericity of non-positive curvature); see classical theorems, especially on Pinched sectional curvature and Positive curvature.
The above statements are made more precise below.
, which can be any natural number
.
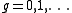By "discretely classified" we mean that for a given genus, there is a connected, irreducible moduli space
of curves of that genus.
The Kodaira dimension of an algebraic curve is:
Compare with the Uniformization theorem
for surfaces (real surfaces, which are the analogue in differential geometry of algebraic curves): Kodaira dimension -1 corresponds to positive curvature, Kodaira dimension 0 corresponds to flat, Kodaira dimension 1 corresponds to negative curvature. Note that the generic surface is of general type: in the moduli space of surfaces, 2 components have Kodaira dimension below 1, while all other components have Kodaira dimension 1. Further, the component corresponding to genus 0 is a point, to genus 1 is 1-dimensional, and to genus
is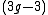 
-dimensional.
classifies surfaces: coarsely by Kodaira dimension, then in more detail within a given dimension.
and Calabi-Yau manifolds (in dimension 1, elliptic curve
s; in dimension 2, complex tori and K3 surface
s) have Kodaira dimension zero (corresponding to admitting flat metrics and Ricci flat metrics, respectively).
Equivalently, K is a big line bundle
; equivalently, the n-canonical map is
generically injective for n sufficiently large.
For example, a variety with ample canonical bundle is of general type.
In some sense varieties of general type are generic, hence the term
(discrete invariants of varieties of general type vary in more dimensions, and moduli space of varieties of general type have more dimensions; this is made more precise for curves and surfaces). A smooth hypersurface of degree d in the n-dimensional projective space is of general type if and only if d is greater than n+1. In this sense most smooth
hypersurfaces in the complex projective space are of general type.
Varieties of general type seem too complicated to classify explicitly, even for surfaces.
proved invariance of plurigenera under deformations for varieties of general type.
to the pluricanonical ring should produce a projective variety in which the sections of powers of K 'capture' as much as they can about V.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, the Kodaira dimension κ(V) measures the size of the canonical model
Canonical Model
Canonical Model is a design pattern used to communicate between different data formats. A form of Enterprise Application Integration, it is intended to reduce costs and standardize on agreed data definitions associated with integrating business systems. A Canonical Model is any model that is...
of a projective variety V.
The definition of Kodaira dimension, named for Kunihiko Kodaira, and the notation κ were introduced in the seminar
.
The plurigenera
The dimension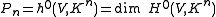is the classically-defined n-th plurigenus of V.
The pluricanonical divisor
, via the corresponding linear system of divisorsLinear system of divisors
In algebraic geometry, a linear system of divisors is an algebraic generalization of the geometric notion of a family of curves; the dimension of the linear system corresponds to the number of parameters of the family....
, gives a map to projective space
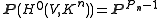,called the n-canonical map.
Kodaira dimension
The canonical ring R=R(K) of a variety V is the graded ring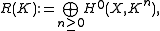where K is a canonical divisor of V. The projective dimension of R(K) is called the Kodaira dimension.
Definition
The following are equivalent:- The dimension of the Proj constructionProj constructionIn algebraic geometry, Proj is a construction analogous to the spectrum-of-a-ring construction of affine schemes, which produces objects with the typical properties of projective spaces and projective varieties...
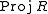(this variety is called the canonical model of V).
- The dimension of the image of the n-canonical mapping for n large enough.
- The transcendence degreeTranscendence degreeIn abstract algebra, the transcendence degree of a field extension L /K is a certain rather coarse measure of the "size" of the extension...
of R, minus one, i.e. t − 1, where t is the number of algebraically independent generators one can find.
- The rate of growth of the plurigenera: it is the smallest number κ such that
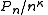is bounded. In Big O notationBig O notationIn mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
, it is the minimal κ such that
.
Conventionally, when R is trivial (
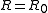= underlying field (constant functions); the plurigenera are all zero (other than 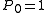); the pluricanonical divisors are not effective), which happens for example when V is rational, one takes (in agreement with the transcendence degree definition), or sometimes 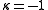(which is a conventional dimension of the empty set, as it preserves additivity under multiplication).Kodaira dimensions can take any value from −1 to the dimension
Dimension of an algebraic variety
In mathematics, the dimension of an algebraic variety V in algebraic geometry is defined, informally speaking, as the number of independent rational functions that exist on V.For example, an algebraic curve has by definition dimension 1...
of V.
Application
The Kodaira dimension is a relatively coarse invariant, and helps to give the outline for the classification of algebraic varieties: it is coarse in that there are generally several distinct families of varieties with a given Kodaira dimension.Varieties with low Kodaira dimension are special, while varieties of maximal Kodaira dimension are (suggestively) called general type.
Geometrically, there is a rough correspondence between Kodaira dimension and curvature: negative Kodaira dimension corresponds to positive curvature, zero Kodaira dimension corresponds to flatness, and maximum Kodaira dimension (general type) corresponds to negative curvature.
The specialness of varieties of low Kodaira dimension corresponds to the specialness of Riemannian manifolds of positive curvature (and general type corresponds to the genericity of non-positive curvature); see classical theorems, especially on Pinched sectional curvature and Positive curvature.
The above statements are made more precise below.
Dimension 1
Complex non-singular algebraic curves are discretely classified by genusGenus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
, which can be any natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
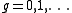.By "discretely classified" we mean that for a given genus, there is a connected, irreducible moduli space
Moduli space
In algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
of curves of that genus.
The Kodaira dimension of an algebraic curve is:
-
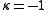: genus 0 (projective lineProjective lineIn mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see...
): K is not effective,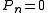
-
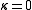: genus 1 (elliptic curveElliptic curveIn mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s): K is a trivial bundle,
-
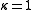: genus 2 or more: K is ample.
Compare with the Uniformization theorem
Uniformization theorem
In mathematics, the uniformization theorem says that any simply connected Riemann surface is conformally equivalent to one of the three domains: the open unit disk, the complex plane, or the Riemann sphere. In particular it admits a Riemannian metric of constant curvature...
for surfaces (real surfaces, which are the analogue in differential geometry of algebraic curves): Kodaira dimension -1 corresponds to positive curvature, Kodaira dimension 0 corresponds to flat, Kodaira dimension 1 corresponds to negative curvature. Note that the generic surface is of general type: in the moduli space of surfaces, 2 components have Kodaira dimension below 1, while all other components have Kodaira dimension 1. Further, the component corresponding to genus 0 is a point, to genus 1 is 1-dimensional, and to genus
is 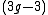-dimensional.Dimension 2
The Enriques-Kodaira classificationEnriques-Kodaira classification
In mathematics, the Enriques–Kodaira classification is a classification of compact complex surfaces into ten classes. For each of these classes, the surfaces in the class can be parametrized by a moduli space...
classifies surfaces: coarsely by Kodaira dimension, then in more detail within a given dimension.
General dimension
Rational varieties have negative Kodaira dimension (corresponding to positive curvature). Abelian varietiesAbelian variety
In mathematics, particularly in algebraic geometry, complex analysis and number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions...
and Calabi-Yau manifolds (in dimension 1, elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s; in dimension 2, complex tori and K3 surface
K3 surface
In mathematics, a K3 surface is a complex or algebraic smooth minimal complete surface that is regular and has trivial canonical bundle.In the Enriques-Kodaira classification of surfaces they form one of the 5 classes of surfaces of Kodaira dimension 0....
s) have Kodaira dimension zero (corresponding to admitting flat metrics and Ricci flat metrics, respectively).
General type
A variety of general type V is one of maximal Kodaira dimension (Kodaira dimension equal to its dimension):Equivalently, K is a big line bundle
Line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
; equivalently, the n-canonical map is
generically injective for n sufficiently large.
For example, a variety with ample canonical bundle is of general type.
In some sense varieties of general type are generic, hence the term
(discrete invariants of varieties of general type vary in more dimensions, and moduli space of varieties of general type have more dimensions; this is made more precise for curves and surfaces). A smooth hypersurface of degree d in the n-dimensional projective space is of general type if and only if d is greater than n+1. In this sense most smooth
hypersurfaces in the complex projective space are of general type.
Varieties of general type seem too complicated to classify explicitly, even for surfaces.
proved invariance of plurigenera under deformations for varieties of general type.
Application to classification
The Iitaka conjecture states that the Kodaira dimension of a fibration is at least the sum of the Kodaira dimension of the base and the Kodaira dimension of a general fiber. This motivates a classification programme for algebraic varieties, in which it is sought to represent V as a fibration over a variety of general type, with typical fiber of Kodaira dimension 0. This is quite a natural idea, given that the application of the Proj constructionProj construction
In algebraic geometry, Proj is a construction analogous to the spectrum-of-a-ring construction of affine schemes, which produces objects with the typical properties of projective spaces and projective varieties...
to the pluricanonical ring should produce a projective variety in which the sections of powers of K 'capture' as much as they can about V.