
Elliptic complex
Encyclopedia
In mathematics
, in particular in partial differential equation
s and differential geometry, an elliptic complex generalizes the notion of an elliptic operator
to sequences. Elliptic complexes isolate those features common to the de Rham complex
and the Dolbeault complex
which are essential for performing Hodge theory
. They also arise in connection with the Atiyah-Singer index theorem and Atiyah-Bott fixed point theorem.
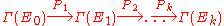
of differential operators between the sheaves
of sections of the Ei such that Pi+1 o Pi=0. A differential complex is elliptic if the sequence of symbols
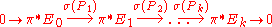
is exact
outside of the zero section. Here π is the projection of the cotangent bundle
T*M to M, and π* is the pullback
of a vector bundle.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in particular in partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s and differential geometry, an elliptic complex generalizes the notion of an elliptic operator
Elliptic operator
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
to sequences. Elliptic complexes isolate those features common to the de Rham complex
De Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
and the Dolbeault complex
Dolbeault cohomology
In mathematics, in particular in algebraic geometry and differential geometry, Dolbeault cohomology is an analog of de Rham cohomology for complex manifolds. Let M be a complex manifold...
which are essential for performing Hodge theory
Hodge theory
In mathematics, Hodge theory, named after W. V. D. Hodge, is one aspect of the study of the algebraic topology of a smooth manifold M. More specifically, it works out the consequences for the cohomology groups of M, with real coefficients, of the partial differential equation theory of generalised...
. They also arise in connection with the Atiyah-Singer index theorem and Atiyah-Bott fixed point theorem.
Definition
If E0, E1, ..., Ek are vector bundles on a smooth manifold M (usually taken to be compact), then a differential complex is a sequence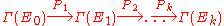
of differential operators between the sheaves
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of sections of the Ei such that Pi+1 o Pi=0. A differential complex is elliptic if the sequence of symbols
Symbol of a differential operator
In mathematics, the symbol of a linear differential operator associates to a differential operator a polynomial by, roughly speaking, replacing each partial derivative by a new variable. The symbol of a differential operator has broad applications to Fourier analysis. In particular, in this...
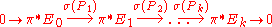
is exact
Exact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
outside of the zero section. Here π is the projection of the cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
T*M to M, and π* is the pullback
Pullback bundle
In mathematics, a pullback bundle or induced bundle is a useful construction in the theory of fiber bundles. Given a fiber bundle π : E → B and a continuous map f : B′ → B one can define a "pullback" of E by f as a bundle f*E over B′...
of a vector bundle.

