
Dirichlet convolution
Encyclopedia
In mathematics
, the Dirichlet convolution is a binary operation
defined for arithmetic function
s; it is important in number theory
. It was developed by Johann Peter Gustav Lejeune Dirichlet
, a German mathematician.
s to the complex number
s), one defines a new arithmetic function ƒ * g, the Dirichlet convolution of ƒ and g, by

where the sum extends over all positive divisor
s d of n.
, the , under pointwise addition and Dirichlet convolution, with the multiplicative identity given by the function defined by
defined by  (n) = 1 if n = 1 and
(n) = 1 if n = 1 and  (n) = 0 if n > 1. The unit
(n) = 0 if n > 1. The unit
s of this ring are the arithmetic functions f with f(1) ≠ 0.
Specifically, Dirichlet convolution is associative
,
distributes
over addition
and is commutative
,
Furthermore,
and for each f for which f(1) ≠ 0 there exists a g such that f * g = , called the of f.
, called the of f.
The Dirichlet convolution of two multiplicative function
s is again multiplicative, and every multiplicative function has a Dirichlet inverse that is also multiplicative. The article on multiplicative functions lists several convolution relations among important multiplicative functions.
Given a completely multiplicative function
f then f (g*h) = (f g)*(f h). The convolution of two completely multiplicative functions need not be completely multiplicative.

and for n > 1,

When ƒ(n) = 1 for all n, then the inverse is ƒ −1(n) = μ(n), the Möbius function
. The Möbius inversion formula
is the special case of the Dirichlet inversion which is valid for completely multiplicative functions, like f(n)=1.
by
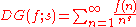
for those complex
arguments s for which the series converges (if there are any). The multiplication of Dirichlet series is compatible with Dirichlet convolution in the following sense:

for all s for which both series of the left hand side converge, one of them at least converging
absolutely (note that simple convergence of both series of the left hand side DOES NOT imply convergence of the right hand side!). This is akin to the convolution theorem
if one thinks of Dirichlet series as a Fourier transform
.
operations which share many features with the Dirichlet convolution (existence
of a Möbius inversion, persistence of multiplicativity, definitions
of totients, Euler-type product formulas over associated primes,...).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Dirichlet convolution is a binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
defined for arithmetic function
Arithmetic function
In number theory, an arithmetic function is a real or complex valued function ƒ defined on the set of natural numbers In number theory, an arithmetic (or arithmetical) function is a real or complex valued function ƒ(n) defined on the set of natural numbers In number theory, an arithmetic (or...
s; it is important in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
. It was developed by Johann Peter Gustav Lejeune Dirichlet
Johann Peter Gustav Lejeune Dirichlet
Johann Peter Gustav Lejeune Dirichlet was a German mathematician with deep contributions to number theory , as well as to the theory of Fourier series and other topics in mathematical analysis; he is credited with being one of the first mathematicians to give the modern formal definition of a...
, a German mathematician.
Definition
If ƒ and g are two arithmetic functions (i.e. functions from the positive integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s to the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s), one defines a new arithmetic function ƒ * g, the Dirichlet convolution of ƒ and g, by

where the sum extends over all positive divisor
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
s d of n.
Properties
The set of arithmetic functions forms a commutative ringCommutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
, the , under pointwise addition and Dirichlet convolution, with the multiplicative identity given by the function
 defined by
defined by  (n) = 1 if n = 1 and
(n) = 1 if n = 1 and  (n) = 0 if n > 1. The unit
(n) = 0 if n > 1. The unitUnit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
s of this ring are the arithmetic functions f with f(1) ≠ 0.
Specifically, Dirichlet convolution is associative
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
,
- (f * g) * h = f * (g * h),
distributes
Distributivity
In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
over addition
- f * (g + h) = f * g + f * h = (g + h) * f,
and is commutative
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
,
- f * g = g * f.
Furthermore,
- f *
 =
=  * f = f,
* f = f,
and for each f for which f(1) ≠ 0 there exists a g such that f * g =
 , called the of f.
, called the of f.The Dirichlet convolution of two multiplicative function
Multiplicative function
In number theory, a multiplicative function is an arithmetic function f of the positive integer n with the property that f = 1 and whenevera and b are coprime, then...
s is again multiplicative, and every multiplicative function has a Dirichlet inverse that is also multiplicative. The article on multiplicative functions lists several convolution relations among important multiplicative functions.
Given a completely multiplicative function
Completely multiplicative function
In number theory, functions of positive integers which respect products are important and are called completely multiplicative functions or totally multiplicative functions. Especially in number theory, a weaker condition is also important, respecting only products of coprime numbers, and such...
f then f (g*h) = (f g)*(f h). The convolution of two completely multiplicative functions need not be completely multiplicative.
Dirichlet inverse
Given an arithmetic function ƒ, an explicit recursive formula for the Dirichlet inverse may be given as follows:
and for n > 1,

When ƒ(n) = 1 for all n, then the inverse is ƒ −1(n) = μ(n), the Möbius function
Möbius function
The classical Möbius function μ is an important multiplicative function in number theory and combinatorics. The German mathematician August Ferdinand Möbius introduced it in 1832...
. The Möbius inversion formula
Möbius inversion formula
In mathematics, the classic Möbius inversion formula was introduced into number theory during the 19th century by August Ferdinand Möbius. Other Möbius inversion formulas are obtained when different local finite partially ordered sets replace the classic case of the natural numbers ordered by...
is the special case of the Dirichlet inversion which is valid for completely multiplicative functions, like f(n)=1.
Dirichlet series
If f is an arithmetic function, one defines its Dirichlet series generating functionGenerating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
by
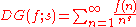
for those complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
arguments s for which the series converges (if there are any). The multiplication of Dirichlet series is compatible with Dirichlet convolution in the following sense:

for all s for which both series of the left hand side converge, one of them at least converging
absolutely (note that simple convergence of both series of the left hand side DOES NOT imply convergence of the right hand side!). This is akin to the convolution theorem
Convolution theorem
In mathematics, the convolution theorem states that under suitableconditions the Fourier transform of a convolution is the pointwise product of Fourier transforms. In other words, convolution in one domain equals point-wise multiplication in the other domain...
if one thinks of Dirichlet series as a Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
.
Related Concepts
The restriction of the divisors in the convolution to unitary, bi-unitary or infinitary divisors defines similar commutativeoperations which share many features with the Dirichlet convolution (existence
of a Möbius inversion, persistence of multiplicativity, definitions
of totients, Euler-type product formulas over associated primes,...).

