Derived functor
Encyclopedia
In mathematics
, certain functor
s may be derived to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics.
Suppose we are given a covariant left exact functor F : A → B between two abelian categories
A and B. If 0 → A → B → C → 0 is a short exact sequence in A, then applying F yields the exact sequence 0 → F(A) → F(B) → F(C) and one could ask how to continue this sequence to the right to form a long exact sequence. Strictly speaking, this question is ill-posed, since there are always numerous different ways to continue a given exact sequence to the right. But it turns out that (if A is "nice" enough) there is one canonical way of doing so, given by the right derived functors of F. For every i≥1, there is a functor RiF: A → B, and the above sequence continues like so: 0 → F(A) → F(B) → F(C) → R1F(A) → R1F(B) → R1F(C) → R2F(A) → R2F(B) → ... . From this we see that F is an exact functor if and only if R1F = 0; so in a sense the right derived functors of F measure "how far" F is from being exact.
If the object A in the above short exact sequence is injective
, then the sequence splits
. Applying any additive functor to a split sequence results in a split sequence, so in particular R1F(A) = 0. Right derived functors are zero on injectives: this is the motivation for the construction given below.
A → I where I is an injective object
in A.
The right derived functors of the covariant left-exact functor F : A → B are then defined as follows. Start with an object X of A. Because there are enough injectives, we can construct a long exact sequence of the form
where the I i are all injective (this is known as an injective resolution of X). Applying the functor F to this sequence, and chopping off the first term, we obtain the chain complex

Note: this is in general not an exact sequence anymore. But we can compute its homology
at the i-th spot (the kernel of the map from F(Ii) modulo the image of the map to F(Ii)); we call the result RiF(X). Of course, various things have to be checked: the end result does not depend on the given injective resolution of X, and any morphism X → Y naturally yields a morphism RiF(X) → RiF(Y), so that we indeed obtain a functor. Note that left exactness means that
0 →F(X) → F(I0) → F(I1)
is exact, so R0F(X) = F(X), so we only get something interesting for i>0.
(Technically, to produce well-defined derivatives of F, we would have to fix an injective resolution for every object of A. This choice of injective resolutions then yields functors RiF. Different choices of resolutions yield naturally isomorphic functors, so in the end the choice doesn't really matter.)
The above-mentioned property of turning short exact sequences into long exact sequences is a consequence of the snake lemma
.
If X is itself injective, then we can choose the injective resolution 0 → X → X → 0, and we obtain that RiF(X) = 0 for all i ≥ 1. In practice, this fact, together with the long exact sequence property, is often used to compute the values of right derived functors.
An equivalent way to compute RiF(X) is the following: take an injective resolution of X as above, and let Ki be the image of the map Ii-1→Ii (for i=0, define Ii-1=0), which is the same as the kernel of Ii→Ii+1. Let φi : Ii-1→Ki be the corresponding surjective map. Then RiF(X) is the cokernel of F(φi).
), then one can define analogously the left-derived functors LiG. For an object X of A we first construct a projective resolution of the form
where the Pi are projective. We apply G to this sequence, chop off the last term, and compute homology to get LiG(X). As before, L0G(X) = G(X).
In this case, the long exact sequence will grow "to the left" rather than to the right:
is turned into .
.
Left derived functors are zero on all projective objects.
One may also start with a contravariant left-exact functor F; the resulting right-derived functors are then also contravariant. The short exact sequence

is turned into the long exact sequence

These right derived functors are zero on projectives and are therefore computed via projective resolutions.
, then the category of all sheaves
of abelian group
s on X is an abelian category with enough injectives. The functor which assigns to each such sheaf L the group L(X) of global sections is left exact, and the right derived functors are the sheaf cohomology
functors, usually written as H i(X,L). Slightly more generally: if (X, OX) is a ringed space
, then the category of all sheaves of OX-modules is an abelian category with enough injectives, and we can again construct sheaf cohomology as the right derived functors of the global section functor.
Étale cohomology
is another cohomology theory for sheaves over a scheme.
Ext functors. If R is a ring
, then the category of all left R-modules
is an abelian category with enough injectives. If A is a fixed left R-module, then the functor Hom(A,-) is left exact, and its right derived functors are the Ext functor
s ExtRi(A,B).
Tor functors. The category of left R-modules also has enough projectives. If A is a fixed right R-module, then the tensor product
with A gives a right exact covariant functor on the category of left R-modules; its left derivatives are the Tor functor
s TorRi(A,B).
Group cohomology. Let G be a group
. A G-module
M is an abelian group
M together with a group action
of G on M as a group of automorphisms. This is the same as a module
over the group ring
ZG. The G-modules form an abelian category with enough injectives. We write MG for the subgroup of M consisting of all elements of M that are held fixed by G. This is a left-exact functor, and its right derived functors are the group cohomology
functors, typically written as H i(G,M).
First, given a commutative diagram
of the form

(where the rows are exact), the two resulting long exact sequences are related by commuting squares:

Second, suppose η : F → G is a natural transformation
from the left exact functor F to the left exact functor G. Then natural transformations Riη : RiF → RiG are induced, and indeed Ri becomes a functor from the functor category
of all left exact functors from A to B to the full functor category of all functors from A to B. Furthermore, this functor is compatible with the long exact sequences in the following sense: if
is a short exact sequence, then a commutative diagram
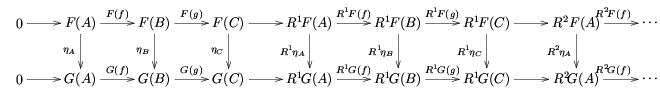
is induced.
Both of these naturalities follow from the naturality of the sequence provided by the snake lemma
.
Conversely, the following characterization of derived functors holds: given a family of functors Ri: A → B, satisfying the above, i.e. mapping short exact sequences to long exact sequences, such that for every injective object I of A, Ri(I)=0 for every positive i, then these functors are the right derived functors of R0.
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, certain functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
s may be derived to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics.
Motivation
It was noted in various quite different settings that a short exact sequence often gives rise to a "long exact sequence". The concept of derived functors explains and clarifies many of these observations.Suppose we are given a covariant left exact functor F : A → B between two abelian categories
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
A and B. If 0 → A → B → C → 0 is a short exact sequence in A, then applying F yields the exact sequence 0 → F(A) → F(B) → F(C) and one could ask how to continue this sequence to the right to form a long exact sequence. Strictly speaking, this question is ill-posed, since there are always numerous different ways to continue a given exact sequence to the right. But it turns out that (if A is "nice" enough) there is one canonical way of doing so, given by the right derived functors of F. For every i≥1, there is a functor RiF: A → B, and the above sequence continues like so: 0 → F(A) → F(B) → F(C) → R1F(A) → R1F(B) → R1F(C) → R2F(A) → R2F(B) → ... . From this we see that F is an exact functor if and only if R1F = 0; so in a sense the right derived functors of F measure "how far" F is from being exact.
If the object A in the above short exact sequence is injective
Injective object
In mathematics, especially in the field of category theory, the concept of injective object is a generalization of the concept of injective module. This concept is important in homotopy theory and in theory of model categories...
, then the sequence splits
Splitting lemma
In mathematics, and more specifically in homological algebra, the splitting lemma states that in any abelian category, the following statements for short exact sequence are equivalent....
. Applying any additive functor to a split sequence results in a split sequence, so in particular R1F(A) = 0. Right derived functors are zero on injectives: this is the motivation for the construction given below.
Construction and first properties
The crucial assumption we need to make about our abelian category A is that it has enough injectives, meaning that for every object A in A there exists a monomorphismMonomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
A → I where I is an injective object
Injective object
In mathematics, especially in the field of category theory, the concept of injective object is a generalization of the concept of injective module. This concept is important in homotopy theory and in theory of model categories...
in A.
The right derived functors of the covariant left-exact functor F : A → B are then defined as follows. Start with an object X of A. Because there are enough injectives, we can construct a long exact sequence of the form

where the I i are all injective (this is known as an injective resolution of X). Applying the functor F to this sequence, and chopping off the first term, we obtain the chain complex
Chain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...

Note: this is in general not an exact sequence anymore. But we can compute its homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
at the i-th spot (the kernel of the map from F(Ii) modulo the image of the map to F(Ii)); we call the result RiF(X). Of course, various things have to be checked: the end result does not depend on the given injective resolution of X, and any morphism X → Y naturally yields a morphism RiF(X) → RiF(Y), so that we indeed obtain a functor. Note that left exactness means that
0 →F(X) → F(I0) → F(I1)
is exact, so R0F(X) = F(X), so we only get something interesting for i>0.
(Technically, to produce well-defined derivatives of F, we would have to fix an injective resolution for every object of A. This choice of injective resolutions then yields functors RiF. Different choices of resolutions yield naturally isomorphic functors, so in the end the choice doesn't really matter.)
The above-mentioned property of turning short exact sequences into long exact sequences is a consequence of the snake lemma
Snake lemma
The snake lemma is a tool used in mathematics, particularly homological algebra, to construct long exact sequences. The snake lemma is valid in every abelian category and is a crucial tool in homological algebra and its applications, for instance in algebraic topology...
.
If X is itself injective, then we can choose the injective resolution 0 → X → X → 0, and we obtain that RiF(X) = 0 for all i ≥ 1. In practice, this fact, together with the long exact sequence property, is often used to compute the values of right derived functors.
An equivalent way to compute RiF(X) is the following: take an injective resolution of X as above, and let Ki be the image of the map Ii-1→Ii (for i=0, define Ii-1=0), which is the same as the kernel of Ii→Ii+1. Let φi : Ii-1→Ki be the corresponding surjective map. Then RiF(X) is the cokernel of F(φi).
Variations
If one starts with a covariant right-exact functor G, and the category A has enough projectives (i.e. for every object A of A there exists an epimorphism P → A where P is a projective objectProjective module
In mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
), then one can define analogously the left-derived functors LiG. For an object X of A we first construct a projective resolution of the form

where the Pi are projective. We apply G to this sequence, chop off the last term, and compute homology to get LiG(X). As before, L0G(X) = G(X).
In this case, the long exact sequence will grow "to the left" rather than to the right:

is turned into
 .
.Left derived functors are zero on all projective objects.
One may also start with a contravariant left-exact functor F; the resulting right-derived functors are then also contravariant. The short exact sequence

is turned into the long exact sequence

These right derived functors are zero on projectives and are therefore computed via projective resolutions.
Applications
Sheaf cohomology. If X is a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, then the category of all sheaves
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s on X is an abelian category with enough injectives. The functor which assigns to each such sheaf L the group L(X) of global sections is left exact, and the right derived functors are the sheaf cohomology
Sheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
functors, usually written as H i(X,L). Slightly more generally: if (X, OX) is a ringed space
Ringed space
In mathematics, a ringed space is, intuitively speaking, a space together with a collection of commutative rings, the elements of which are "functions" on each open set of the space...
, then the category of all sheaves of OX-modules is an abelian category with enough injectives, and we can again construct sheaf cohomology as the right derived functors of the global section functor.
Étale cohomology
Étale cohomology
In mathematics, the étale cohomology groups of an algebraic variety or scheme are algebraic analogues of the usual cohomology groups with finite coefficients of a topological space, introduced by Grothendieck in order to prove the Weil conjectures...
is another cohomology theory for sheaves over a scheme.
Ext functors. If R is a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, then the category of all left R-modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
is an abelian category with enough injectives. If A is a fixed left R-module, then the functor Hom(A,-) is left exact, and its right derived functors are the Ext functor
Ext functor
In mathematics, the Ext functors of homological algebra are derived functors of Hom functors. They were first used in algebraic topology, but are common in many areas of mathematics.- Definition and computation :...
s ExtRi(A,B).
Tor functors. The category of left R-modules also has enough projectives. If A is a fixed right R-module, then the tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
with A gives a right exact covariant functor on the category of left R-modules; its left derivatives are the Tor functor
Tor functor
In homological algebra, the Tor functors are the derived functors of the tensor product functor. They were first defined in generality to express the Künneth theorem and universal coefficient theorem in algebraic topology....
s TorRi(A,B).
Group cohomology. Let G be a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. A G-module
G-module
In mathematics, given a group G, a G-module is an abelian group M on which G acts compatibly with the abelian group structure on M. This widely applicable notion generalizes that of a representation of G...
M is an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
M together with a group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of G on M as a group of automorphisms. This is the same as a module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over the group ring
Group ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
ZG. The G-modules form an abelian category with enough injectives. We write MG for the subgroup of M consisting of all elements of M that are held fixed by G. This is a left-exact functor, and its right derived functors are the group cohomology
Group cohomology
In abstract algebra, homological algebra, algebraic topology and algebraic number theory, as well as in applications to group theory proper, group cohomology is a way to study groups using a sequence of functors H n. The study of fixed points of groups acting on modules and quotient modules...
functors, typically written as H i(G,M).
Naturality
Derived functors and the long exact sequences are "natural" in several technical senses.First, given a commutative diagram
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
of the form

(where the rows are exact), the two resulting long exact sequences are related by commuting squares:

Second, suppose η : F → G is a natural transformation
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
from the left exact functor F to the left exact functor G. Then natural transformations Riη : RiF → RiG are induced, and indeed Ri becomes a functor from the functor category
Functor category
In category theory, a branch of mathematics, the functors between two given categories form a category, where the objects are the functors and the morphisms are natural transformations between the functors...
of all left exact functors from A to B to the full functor category of all functors from A to B. Furthermore, this functor is compatible with the long exact sequences in the following sense: if

is a short exact sequence, then a commutative diagram
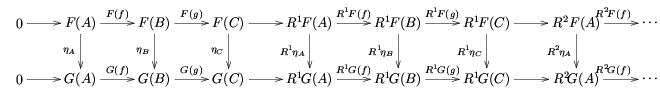
is induced.
Both of these naturalities follow from the naturality of the sequence provided by the snake lemma
Snake lemma
The snake lemma is a tool used in mathematics, particularly homological algebra, to construct long exact sequences. The snake lemma is valid in every abelian category and is a crucial tool in homological algebra and its applications, for instance in algebraic topology...
.
Conversely, the following characterization of derived functors holds: given a family of functors Ri: A → B, satisfying the above, i.e. mapping short exact sequences to long exact sequences, such that for every injective object I of A, Ri(I)=0 for every positive i, then these functors are the right derived functors of R0.
Generalization
The more modern (and more general) approach to derived functors uses the language of derived categoriesDerived category
In mathematics, the derived category D of an abelian category C is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on C...
.

