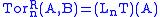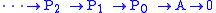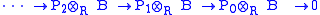Tor functor
Encyclopedia
In homological algebra
, the Tor functors are the derived functor
s of the tensor product
functor. They were first defined in generality to express the Künneth theorem
and universal coefficient theorem
in algebraic topology
.
Specifically, suppose R is a ring
, and denote by R-Mod the category
of left R-modules
and by Mod-R the category of right R-modules (if R is commutative
, the two categories coincide). Pick a fixed module B in R-Mod. For A in Mod-R, set T(A) = A⊗RB. Then T is a right exact functor from Mod-R to the category of abelian groups
Ab (in the case when R is commutative, it is a right exact functor from Mod-R to Mod-R) and its left derived functor
s LnT are defined. We set
i.e., we take a projective resolution
then tensor the projective resolution with B to get the complex
(note that does not appear and the last arrow is just the zero map) and take the homology
does not appear and the last arrow is just the zero map) and take the homology
of this complex.
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
, the Tor functors are the derived functor
Derived functor
In mathematics, certain functors may be derived to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics.- Motivation :...
s of the tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
functor. They were first defined in generality to express the Künneth theorem
Künneth theorem
In mathematics, especially in homological algebra and algebraic topology, a Künneth theorem is a statement relating the homology of two objects to the homology of their product. The classical statement of the Künneth theorem relates the singular homology of two topological spaces X and Y and their...
and universal coefficient theorem
Universal coefficient theorem
In mathematics, the universal coefficient theorem in algebraic topology establishes the relationship in homology theory between the integral homology of a topological space X, and its homology with coefficients in any abelian group A...
in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
.
Specifically, suppose R is a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, and denote by R-Mod the category
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
of left R-modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
and by Mod-R the category of right R-modules (if R is commutative
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
, the two categories coincide). Pick a fixed module B in R-Mod. For A in Mod-R, set T(A) = A⊗RB. Then T is a right exact functor from Mod-R to the category of abelian groups
Category of abelian groups
In mathematics, the category Ab has the abelian groups as objects and group homomorphisms as morphisms. This is the prototype of an abelian category....
Ab (in the case when R is commutative, it is a right exact functor from Mod-R to Mod-R) and its left derived functor
Derived functor
In mathematics, certain functors may be derived to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics.- Motivation :...
s LnT are defined. We set
i.e., we take a projective resolution
then tensor the projective resolution with B to get the complex
(note that
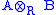 does not appear and the last arrow is just the zero map) and take the homology
does not appear and the last arrow is just the zero map) and take the homologyHomology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
of this complex.
Properties
- For every n ≥ 1, TornR is an additive functor from Mod-R × R-Mod to Ab. In the case when R is commutative, we have additive functors from Mod-R × Mod-R to Mod-R.
- As is true for every family of derived functors, every short exact sequence

induces a long exact sequence of the form
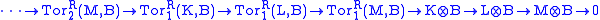 .
.
- If R is commutative and r in R is not a zero divisorZero divisorIn abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
then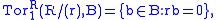
from which the terminology Tor (that is, Torsion) comes: see torsion subgroup
Torsion subgroupIn the theory of abelian groups, the torsion subgroup AT of an abelian group A is the subgroup of A consisting of all elements that have finite order...
.
- In the case of abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s (i.e. if R is the ring of integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s Z), then TornZ(A,B) = 0 for all n ≥ 2. The reason: every abelian group A has a free resolution of length 1, since subgroups of free abelian groupFree abelian groupIn abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
s are free abelian. So in this important special case, the higher Tor functors are invisible. In addition, Tor1Z(Zk,A) = Ker(f) where f represents "multiplication by k".
- Furthermore, every free module has a free resolution of length zero, so by the argument above, if F is a free R-module, then TornR(F,B) = 0 for all n ≥ 1.
- The Tor functors commute with arbitrary direct sumsDirect sum of modulesIn abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
: there is a natural isomorphism . Indeed, the Tor functors even preserve arbitrary colimits.
. Indeed, the Tor functors even preserve arbitrary colimits.
- From the classification of finitely generated abelian groupsFinitely generated abelian groupIn abstract algebra, an abelian group is called finitely generated if there exist finitely many elements x1,...,xs in G such that every x in G can be written in the formwith integers n1,...,ns...
, we know that every finitely generated abelian group is the direct sum of copies of Z and Zk. This together with the previous three points allows us to compute Tor1Z(A, B) whenever A is finitely generated.
- A module M in Mod-R is flatFlat moduleIn Homological algebra, and algebraic geometry, a flat module over a ring R is an R-module M such that taking the tensor product over R with M preserves exact sequences. A module is faithfully flat if taking the tensor product with a sequence produces an exact sequence if and only if the original...
if and only if Tor1R(M, -) = 0. In this case, we even have TornR(M, -) = 0 for all n ≥ 1 . In fact, to compute TornR(A, B), one may use a flat resolution of A or B, instead of a projective resolution (note that a projective resolution is automatically a flat resolution, but the converse isn't true, so allowing flat resolutions is more flexible).