Dehn surgery
Encyclopedia
In topology
, a branch of mathematics, a Dehn surgery, named after Max Dehn
, is a specific construction used to modify 3-manifold
s. The process takes as input a 3-manifold together with a link
. Dehn surgery can be thought of as a two stage process: drilling and Dehn filling.
We can pick two oriented simple closed curve
s m and ℓ on the boundary torus of the 3-manifold that generate the fundamental group of the torus. This gives any simple closed curve
on that torus two coordinates p and q, each coordinate corresponding to the algebraic intersection of the curve with m and ℓ respectively. These coordinates only depend on the homotopy class of 
.
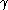We can specify a homeomorphism of the boundary of a solid torus to T by having the meridian curve of the solid torus map to a curve homotopic to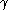
. As long as the meridian maps to the surgery slope 
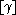, the resulting Dehn surgery will yield a 3-manifold that will not depend on the specific gluing (up to homeomorphism). The ratio p/q is called the surgery coefficient.
In the case of links in the 3-sphere or more generally an oriented homology sphere, there is a canonical choice of the meridians and longitudes of T. The longitude is chosen so that it is null-homologous in the knot complement—equivalently, if it is the boundary of a Seifert surface
. The meridian is the curve that bounds a disc in the tubular neighbourhood of the link. When the ratios p/q are all integers, the surgery is called an integral surgery or a genuine surgery
, since such surgeries are closely related to handlebodies, cobordism
and Morse functions
.
, orientable, connected
3-manifold
is obtained by performing Dehn surgery on a link in the 3-sphere
. This result, the Lickorish-Wallace theorem, was first proven by Wallace in 1960 and independently by Lickorish in a stronger form in 1962. Via the now well-known relation between genuine surgery
and cobordism
, this result is equivalent to the theorem that the oriented cobordism group
of 3-manifolds is trivial, originally due to V. Rohlin in 1951.
Since orientable 3-manifolds can all be generated by suitably decorated links, one might ask how distinct surgery presentations of a given 3-manifold might be related. The answer is called the Kirby calculus
.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, a branch of mathematics, a Dehn surgery, named after Max Dehn
Max Dehn
Max Dehn was a German American mathematician and a student of David Hilbert. He is most famous for his work in geometry, topology and geometric group theory...
, is a specific construction used to modify 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
s. The process takes as input a 3-manifold together with a link
Link (knot theory)
In mathematics, a link is a collection of knots which do not intersect, but which may be linked together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory...
. Dehn surgery can be thought of as a two stage process: drilling and Dehn filling.
Definitions
- Given a 3-manifold3-manifoldIn mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
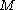and a linkLink (knot theory)In mathematics, a link is a collection of knots which do not intersect, but which may be linked together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory...
, 
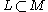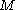drilled along 
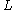is obtained by removing an open tubular neighborhoodTubular neighborhoodIn mathematics, a tubular neighborhood of a submanifold of a smooth manifold is an open set around it resembling the normal bundle.The idea behind a tubular neighborhood can be explained in a simple example. Consider a smooth curve in the plane without self-intersections. On each point on the curve...
of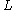
from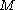 
. 
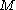drilled along 
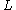is also known as the link complement, since if one removed the corresponding closed tubular neighborhoodTubular neighborhoodIn mathematics, a tubular neighborhood of a submanifold of a smooth manifold is an open set around it resembling the normal bundle.The idea behind a tubular neighborhood can be explained in a simple example. Consider a smooth curve in the plane without self-intersections. On each point on the curve...
from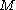
one obtains a manifold diffeomorphic to 
.
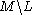- Given a 3-manifold with torus boundary components, we may glue in a solid torusSolid torusIn mathematics, a solid torus is a topological space homeomorphic to S^1 \times D^2, i.e. the cartesian product of the circle with a two dimensional disc endowed with the product topology. The solid torus is a connected, compact, orientable 3-dimensional manifold with boundary...
by a homeomorphismHomeomorphismIn the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
(resp. diffeomorphismDiffeomorphismIn mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
) of its boundary to the torus boundary component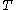
of the original 3-manifold. There are many inequivalent ways of doing this, in general. This process is called Dehn filling.
- Dehn surgery on a 3-manifold containing a link consists of drilling out a tubular neighbourhood of the link together with Dehn filling on all the components of the boundary corresponding to the link.
We can pick two oriented simple closed curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s m and ℓ on the boundary torus of the 3-manifold that generate the fundamental group of the torus. This gives any simple closed curve
on that torus two coordinates p and q, each coordinate corresponding to the algebraic intersection of the curve with m and ℓ respectively. These coordinates only depend on the homotopy class of 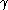.We can specify a homeomorphism of the boundary of a solid torus to T by having the meridian curve of the solid torus map to a curve homotopic to
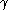. As long as the meridian maps to the surgery slope 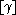, the resulting Dehn surgery will yield a 3-manifold that will not depend on the specific gluing (up to homeomorphism). The ratio p/q is called the surgery coefficient.In the case of links in the 3-sphere or more generally an oriented homology sphere, there is a canonical choice of the meridians and longitudes of T. The longitude is chosen so that it is null-homologous in the knot complement—equivalently, if it is the boundary of a Seifert surface
Seifert surface
In mathematics, a Seifert surface is a surface whose boundary is a given knot or link.Such surfaces can be used to study the properties of the associated knot or link. For example, many knot invariants are most easily calculated using a Seifert surface...
. The meridian is the curve that bounds a disc in the tubular neighbourhood of the link. When the ratios p/q are all integers, the surgery is called an integral surgery or a genuine surgery
Surgery theory
In mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along...
, since such surgeries are closely related to handlebodies, cobordism
Cobordism
In mathematics, cobordism is a fundamental equivalence relation on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold. Two manifolds are cobordant if their disjoint union is the boundary of a manifold one dimension higher. The name comes...
and Morse functions
Morse theory
In differential topology, the techniques of Morse theory give a very direct way of analyzing the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a differentiable function on a manifold will, in a typical case, reflect...
.
Results
Every closedClosed manifold
In mathematics, a closed manifold is a type of topological space, namely a compact manifold without boundary. In contexts where no boundary is possible, any compact manifold is a closed manifold....
, orientable, connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
is obtained by performing Dehn surgery on a link in the 3-sphere
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
. This result, the Lickorish-Wallace theorem, was first proven by Wallace in 1960 and independently by Lickorish in a stronger form in 1962. Via the now well-known relation between genuine surgery
Surgery theory
In mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along...
and cobordism
Cobordism
In mathematics, cobordism is a fundamental equivalence relation on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold. Two manifolds are cobordant if their disjoint union is the boundary of a manifold one dimension higher. The name comes...
, this result is equivalent to the theorem that the oriented cobordism group
Cobordism
In mathematics, cobordism is a fundamental equivalence relation on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold. Two manifolds are cobordant if their disjoint union is the boundary of a manifold one dimension higher. The name comes...
of 3-manifolds is trivial, originally due to V. Rohlin in 1951.
Since orientable 3-manifolds can all be generated by suitably decorated links, one might ask how distinct surgery presentations of a given 3-manifold might be related. The answer is called the Kirby calculus
Kirby calculus
In mathematics, the Kirby calculus in geometric topology, named after Robion Kirby, is a method for modifying framed links in the 3-sphere using a finite set of moves, the Kirby moves...
.
See also
- Hyperbolic Dehn surgeryHyperbolic Dehn surgeryIn mathematics, hyperbolic Dehn surgery is an operation by which one can obtain further hyperbolic 3-manifolds from a given cusped hyperbolic 3-manifold...
- Tubular neighborhoodTubular neighborhoodIn mathematics, a tubular neighborhood of a submanifold of a smooth manifold is an open set around it resembling the normal bundle.The idea behind a tubular neighborhood can be explained in a simple example. Consider a smooth curve in the plane without self-intersections. On each point on the curve...
- SurgerySurgery theoryIn mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along...
on manifolds, in the general sense, also called spherical modification.