Cubic field
Encyclopedia
In mathematics
, specifically the area of algebraic number theory
, a cubic field is an algebraic number field
of degree three.
of the rational numbers Q of degree
[K:Q] = 3, then K is called a cubic field. Any such field is isomorphic to a field of the form
where f is an irreducible cubic
polynomial
with coefficients in Q. If f has three real
roots, then K is called a totally real cubic field and it is an example of a totally real field. If, on the other hand, f has a non-real root, then K is called a complex cubic field.
A cubic field K is called a cyclic cubic field, if it contains all three roots of its generating polynomial f. Equivalently, if it is a Galois extension
of Q, in which case its Galois group
over Q is cyclic
of order three. This can only happen if K is totally real. It is a rare occurrence in the sense that if the set of cubic fields is ordered by discriminant
, then the proportion of cubic fields which are cyclic approaches zero as the bound on the discriminant approaches infinity.
A cubic field is called a pure cubic field, if it can be obtained by adjoining the real cube root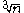
of a cubefree positive integer n to the rational number field Q. This can only occur if K is complex.
However, any other cubic field K is a non-galois extension of Q and has a field extension N of degree two as its Galois closure. The Galois group Gal(N/Q) is isomorphic to the symmetric group
S3 on three letters.
. Then, K is cyclic if, and only if, d = 1, in which case the only subfield of K is Q itself. If d ≠ 1, then the Galois closure N of K contains a unique quadratic field
k whose discriminant is d (in the case d = 1, the subfield Q is sometimes considered as the "degenerate" quadratic field of discriminant 1). The conductor
of N over k is f, and f 2 is the relative discriminant of N over k. The discriminant of N is d3f 4.
The field K is a pure cubic field if, and only if, d = −3. This is the case for which the quadratic field contained in the Galois closure of K is the cyclotomic field of cube roots of unity.
of a number field K is (−1)r2, where r2 is the number of conjugate pairs of complex embeddings of K into C, the discriminant of a cubic field will be positive precisely when the field is totally real, and negative if it is a complex cubic field.
Given some real number N > 0 there are only finitely many cubic fields K whose discriminant DK satisfies |DK| ≤ N. Formulae are known which calculate the prime decomposition of DK, and so it can be explicitly calculated.
However, it should be pointed out that, different from quadratic fields, several non-isomorphic cubic fields
may share the same discriminant D. The number m of these fields is called the multiplicity
of the discriminant D.
Some small examples are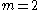
for 
, 
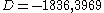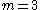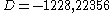for 
, 
for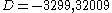 
, and 
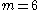for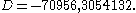 
Any cubic field K will be of the form K = Q(θ) for some number θ that is a root of the irreducible polynomial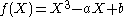
with a and b both being integers. The discriminant
of f is Δ = 4a3 − 27b2. Denoting the discriminant of K by D, the index i(θ) of θ is then defined by Δ = i(θ)2D.
In the case of a non-cyclic cubic field K this index formula can be combined with the conductor formula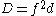
to obtain a decomposition of the polynomial discriminant 
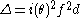into the square of the product 
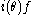and the discriminant d of the quadratic field k associated with the cubic field K, where d is squarefree up to a possible factor 
or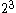 
.
Georgy Voronoy
gave a method for separating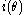
and f in the square part of 
.
The study of the number of cubic fields whose discriminant is less than a given bound is a current area of research. Let N+(X) (respectively N−(X)) denote the number of totally real (respectively complex) cubic fields whose discriminant is bounded by X in absolute value. In the early 1970s, Harold Davenport
and Hans Heilbronn
determined the first term of the asymptotic behaviour of N±(X) (i.e. as X goes to infinity). By means of an analysis of the residue
of the Shintani zeta function
, combined with a study of the tables of cubic fields compiled by Karim Belabas and some heuristic
s, David P. Roberts conjectured a more precise asymptotic formula:
where A± = 1 or 3, B± = 1 or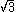
, according to the totally real or complex case, ζ(s) is the Riemann zeta function, and Γ(s) is the Gamma function
. A proof of this formula has been announced by .
, the torsionfree unit rank r of an algebraic number field K with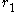
real embeddings and 
pairs of conjugate complex embeddings is determined by the formula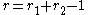 
.
Hence a totally real cubic field K with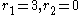
has two independent units 
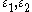and a complex cubic field K with 
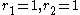has a single fundamental unit 
.
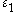These fundamental systems of units can be calculated by means of generalized continued fraction algorithms by Voronoi
, which have been interpreted geometrically by Delone
and Faddeev.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically the area of algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
, a cubic field is an algebraic number field
Algebraic number field
In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
of degree three.
Definition
If K is a field extensionField extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
of the rational numbers Q of degree
Degree of a field extension
In mathematics, more specifically field theory, the degree of a field extension is a rough measure of the "size" of the extension. The concept plays an important role in many parts of mathematics, including algebra and number theory — indeed in any area where fields appear prominently.-...
[K:Q] = 3, then K is called a cubic field. Any such field is isomorphic to a field of the form
where f is an irreducible cubic
Degree of a polynomial
The degree of a polynomial represents the highest degree of a polynominal's terms , should the polynomial be expressed in canonical form . The degree of an individual term is the sum of the exponents acting on the term's variables...
polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
with coefficients in Q. If f has three real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
roots, then K is called a totally real cubic field and it is an example of a totally real field. If, on the other hand, f has a non-real root, then K is called a complex cubic field.
A cubic field K is called a cyclic cubic field, if it contains all three roots of its generating polynomial f. Equivalently, if it is a Galois extension
Galois extension
In mathematics, a Galois extension is an algebraic field extension E/F satisfying certain conditions ; one also says that the extension is Galois. The significance of being a Galois extension is that the extension has a Galois group and obeys the fundamental theorem of Galois theory.The definition...
of Q, in which case its Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
over Q is cyclic
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order three. This can only happen if K is totally real. It is a rare occurrence in the sense that if the set of cubic fields is ordered by discriminant
Discriminant of an algebraic number field
In mathematics, the discriminant of an algebraic number field is a numerical invariant that, loosely speaking, measures the size of the algebraic number field...
, then the proportion of cubic fields which are cyclic approaches zero as the bound on the discriminant approaches infinity.
A cubic field is called a pure cubic field, if it can be obtained by adjoining the real cube root
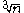of a cubefree positive integer n to the rational number field Q. This can only occur if K is complex.Examples
- Adjoining the real cube root of 2 to the rational numbers gives the cubic field Q(
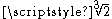). This is an example of a pure cubic field, and hence of a complex cubic field. In fact, of all pure cubic fields, it has the smallest discriminant (in absolute valueAbsolute valueIn mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
), namely −108.
- The complex cubic field obtained by adjoining to Q a root of is not pure. It has the smallest discriminant (in absolute value) of all cubic fields, namely −23.
- Adjoining a root of to Q yields a cyclic cubic field, and hence a totally real cubic field. It has the smallest discriminant of all totally real cubic fields, namely 49.
- The field obtained by adjoining to Q a root of is an example of a totally real cubic field that is not cyclic. Its discriminant is 148, the smallest discriminant of a non-cyclic totally real cubic field.
- No cyclotomic fieldCyclotomic fieldIn number theory, a cyclotomic field is a number field obtained by adjoining a complex primitive root of unity to Q, the field of rational numbers...
s are cubic because the degree of a cyclotomic field is equal to φ(n), where φ is Euler's totient functionEuler's totient functionIn number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
, which only takes on even values (except for φ(1) = φ(2) = 1).
Galois closure
A cyclic cubic field K is its own Galois closure with Galois group Gal(K/Q) isomorphic to the cyclic group of order three.However, any other cubic field K is a non-galois extension of Q and has a field extension N of degree two as its Galois closure. The Galois group Gal(N/Q) is isomorphic to the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
S3 on three letters.
Associated quadratic field
The discriminant of a cubic field K can be written uniquely as df 2 where d is a fundamental discriminantFundamental discriminant
In mathematics, a fundamental discriminant D is an integer invariant in the theory of integral binary quadratic forms. If is a quadratic form with integer coefficients, then is the discriminant of Q. Conversely, every integer D with is the discriminant of some binary quadratic form with integer...
. Then, K is cyclic if, and only if, d = 1, in which case the only subfield of K is Q itself. If d ≠ 1, then the Galois closure N of K contains a unique quadratic field
Quadratic field
In algebraic number theory, a quadratic field is an algebraic number field K of degree two over Q. It is easy to show that the map d ↦ Q is a bijection from the set of all square-free integers d ≠ 0, 1 to the set of all quadratic fields...
k whose discriminant is d (in the case d = 1, the subfield Q is sometimes considered as the "degenerate" quadratic field of discriminant 1). The conductor
Conductor (class field theory)
In algebraic number theory, the conductor of a finite abelian extension of local or global fields provides a quantitative measure of the ramification in the extension. The definition of the conductor is related to the Artin map.-Local conductor:...
of N over k is f, and f 2 is the relative discriminant of N over k. The discriminant of N is d3f 4.
The field K is a pure cubic field if, and only if, d = −3. This is the case for which the quadratic field contained in the Galois closure of K is the cyclotomic field of cube roots of unity.
Discriminant
Since the sign of the discriminantDiscriminant of an algebraic number field
In mathematics, the discriminant of an algebraic number field is a numerical invariant that, loosely speaking, measures the size of the algebraic number field...
of a number field K is (−1)r2, where r2 is the number of conjugate pairs of complex embeddings of K into C, the discriminant of a cubic field will be positive precisely when the field is totally real, and negative if it is a complex cubic field.
Given some real number N > 0 there are only finitely many cubic fields K whose discriminant DK satisfies |DK| ≤ N. Formulae are known which calculate the prime decomposition of DK, and so it can be explicitly calculated.
However, it should be pointed out that, different from quadratic fields, several non-isomorphic cubic fields
may share the same discriminant D. The number m of these fields is called the multiplicityof the discriminant D.
Some small examples are
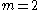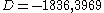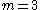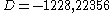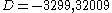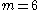for , for , for , and for 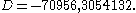Any cubic field K will be of the form K = Q(θ) for some number θ that is a root of the irreducible polynomial
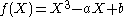
with a and b both being integers. The discriminant
Discriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
of f is Δ = 4a3 − 27b2. Denoting the discriminant of K by D, the index i(θ) of θ is then defined by Δ = i(θ)2D.
In the case of a non-cyclic cubic field K this index formula can be combined with the conductor formula
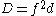to obtain a decomposition of the polynomial discriminant 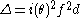into the square of the product 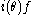and the discriminant d of the quadratic field k associated with the cubic field K, where d is squarefree up to a possible factor or 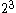.Georgy Voronoy
Georgy Voronoy
Georgy Feodosevich Voronoy was a Russian Empire mathematician of Ukrainian origin. Among other things, he defined the Voronoi diagram.Voronoy was born in the village of Zhuravky, district of Pyriatin, in Poltava Governorate of the Russian Empire .From 1889, Voronoy studied at Saint Petersburg...
gave a method for separating
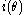and f in the square part of .The study of the number of cubic fields whose discriminant is less than a given bound is a current area of research. Let N+(X) (respectively N−(X)) denote the number of totally real (respectively complex) cubic fields whose discriminant is bounded by X in absolute value. In the early 1970s, Harold Davenport
Harold Davenport
Harold Davenport FRS was an English mathematician, known for his extensive work in number theory.-Early life:...
and Hans Heilbronn
Hans Heilbronn
Hans Arnold Heilbronn was a mathematician.He was born into a German-Jewish family. He was a student at the universities of Berlin, Freiburg and Göttingen, where he met Edmund Landau, who supervised his doctorate...
determined the first term of the asymptotic behaviour of N±(X) (i.e. as X goes to infinity). By means of an analysis of the residue
Residue (complex analysis)
In mathematics, more specifically complex analysis, the residue is a complex number proportional to the contour integral of a meromorphic function along a path enclosing one of its singularities...
of the Shintani zeta function
Shintani zeta function
In mathematics, a Shintani zeta function or Shintani L-function is a generalization of the Riemann zeta function. They were studied studied by...
, combined with a study of the tables of cubic fields compiled by Karim Belabas and some heuristic
Heuristic
Heuristic refers to experience-based techniques for problem solving, learning, and discovery. Heuristic methods are used to speed up the process of finding a satisfactory solution, where an exhaustive search is impractical...
s, David P. Roberts conjectured a more precise asymptotic formula:
where A± = 1 or 3, B± = 1 or
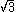, according to the totally real or complex case, ζ(s) is the Riemann zeta function, and Γ(s) is the Gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
. A proof of this formula has been announced by .
Unit group
According to DirichletJohann Peter Gustav Lejeune Dirichlet
Johann Peter Gustav Lejeune Dirichlet was a German mathematician with deep contributions to number theory , as well as to the theory of Fourier series and other topics in mathematical analysis; he is credited with being one of the first mathematicians to give the modern formal definition of a...
, the torsionfree unit rank r of an algebraic number field K with
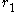real embeddings and pairs of conjugate complex embeddings is determined by the formula 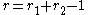.Hence a totally real cubic field K with
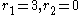has two independent units 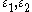and a complex cubic field K with 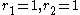has a single fundamental unit 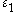.These fundamental systems of units can be calculated by means of generalized continued fraction algorithms by Voronoi
Georgy Voronoy
Georgy Feodosevich Voronoy was a Russian Empire mathematician of Ukrainian origin. Among other things, he defined the Voronoi diagram.Voronoy was born in the village of Zhuravky, district of Pyriatin, in Poltava Governorate of the Russian Empire .From 1889, Voronoy studied at Saint Petersburg...
, which have been interpreted geometrically by Delone
Boris Delaunay
Boris Nikolaevich Delaunay or Delone was one of the first Russian mountain climbers and a Soviet/Russian mathematician, and the father of physicist Nikolai Borisovich Delone....
and Faddeev.